Kapitola 3 Vektorová data

Vektorová data byla poprvé použita v CAD systémech. Jsou vhodná pro měření délek, ploch a pro kartografické výstupy na perovém plotru. Typickými příklady tohoto typu dat jsou formáty DXF, DWG (Autodesk), DGN (Intergraph), IGES (Initial Graphics Exchange Specification), HPGL (Hewlett Packard Graphic Language).

Vektorové vyjádření geografických jevů vystihuje objektivní realitu přesněji než rastrové. Základem vektorové reprezentace dat je předpoklad, že prostor s mapovanými jevy je spojitý. Bodové jevy jsou vyjadřovány body, linie a plochy vyjadřujeme pouze pomocí reprezentativních bodů. Základní topologické entity jsou ve vektorovém formátu vyjádřeny ve formě posloupností kartézských souřadnic x,y jejich reprezentativních bodů. Vzhledem k jemnému rozlišení jejich souřadnicového systému, poskytují pružné a přesné vyjádření objektů. Vektorové struktury umožňují propojení topologie a dalších prostorových vazeb mezi entitami a jevy a jsou proto vhodné pro vyjadřování složitých prostorových struktur, např. sítí (dopravní sítě, říční sítě) nebo těles.

Podstatou vektorových dat je vyjádření geometrické části popisu geoprvku pomocí lineárních charakteristik. Základními prvky vektorových dat jsou:

• Bod - vyjádřen diskrétní polohou určenou souřadnicemi x,y,
• Linie - vyjádřena posloupností orientovaných úseček definovaných souřadnicemi jejich počátečního a koncového bodu,
• Plocha - vyjádřena pomocí uzavřené obrysové linie.

Základní prostorové vztahy mezi těmito prvky byly převzaty z teorie grafů. Graf se skládá ze dvou částí - souborů: uzlů (nodes) a hran (edges). Každá hrana je propojením dvou uzlů. Pokud má význam pořadí uzlů při definování hran, znamená to, že hrana má směr. Mají-li hrany grafu definovaný směr, je graf zorientovaný.

Směr hran a následné zorientování grafu je důležité z více důvodů. Zorientované hrany jsou prostředkem pro definování orientace, směru liniových objektů, pro popis sousednosti (styčnosti) ploch na hranici - nalevo a napravo od hrany. Kromě toho je směr potřebný k popisu ploch, ohraničených spojnicemi rovinného grafu.

Dvě hrany jsou sousedící (přilehlé) - adjacent, mají-li společný uzel. Vyskytuje-li se uzel v \(m\) hranách, pak stupeň - řád tohoto uzlu je \(D(n)=m\). Je-li tedy řád uzlu \(D(n)=0\), uzel se nevyskytuje na žádné spojnici, je to izolovaný uzel - bod.

Za řetěz (chain) označujeme sekvenci sousedících hran, splňuje-li tyto podmínky:

• každá hrana se vyskytuje v určitém řetězu jen jednou
• existují nanejvýš dva uzly, které se vyskytují jen na jedné hraně řetězce. Jejich řád je potom \(D(n)=1\) a jedná se o počáteční a koncový uzel řetězce.
• ostatní uzly v řetězci se vyskytují přesně ve dvou hranách, jejich řád \(D(n)=2\).

Uzavřený řetězec se nazývá polygon, přičemž v polygonu neexistují uzly s řádem \(D(n)=1\), všechny mají řád \(D(n)=2\).

Dva uzly v grafu jsou propojeny, jestliže existuje řetězec, ve kterém se oba vyskytují. Graf je propojený, jestliže jsou všechny možné páry uzlů propojeny. Sdružením více polygonů můžeme vybudovat síť polygonů. Při jejím budování musíme věnovat pozornost:

• neduplicitnímu označení vrcholů a hran,
• zahrnutí všech potřebných bodů a linií,
• rozlišování pravých a levých ploch pro zorientované mapy,
• zohlednění “venkovní” plochy .

Pokrývá-li takováto struktura důsledně celou zkoumanou plochu, nazývá se dělením plochy (area partitioning). Ke kontrole kompletnosti a jednoznačnosti dělení plochy lze použít tzv. Eulerovy rovnice, které sledují vztah mezi počtem uzlů, hran a polygonů. Podle Eulerova pravidla existuje pevný vztah mezi počtem ploch (facet) \(f\), počtem uzlů (nodes) \(n\) a počtem hran (edges) \(e\) v grafu:

\(f+a-e=2\).

Pravidlo v této základní podobě platí pro propojené grafy s plochami bez děr. Pro nepropojené grafy je jej třeba modifikovat:

\(f+a-e=c+1\),

kde \(c\) je počet nespojitých subgrafů.

Na základě výše uvedeného mohou základní stavební prvky pro vektorovou reprezentaci splňovat různé úkoly při reprezentaci různých typů objektů:

• body - uzly mohou mít dvě funkce: mohou fungovat jako počáteční, resp. koncové uzly hran nebo mezilehlé body na liniích (vertexy) - v tomto případě mají mimořádný význam pro definování geometrie a topologie liniových objektů či mohou reprezentovat jednotlivé bodové objekty. Některé body mohou plnit obě funkce najednou. V reprezentaci se mohou vyskytovat i body, které sehrávají jen geometrickou úlohu, ale nereprezentují bodové objekty, ani nejsou uzly.
• hrany - linie mohu plnit také dvě funkce: mohou být součástí reprezentace liniového objektu nebo mohou být součástí hranice mezi dvěma plošnými objekty.

Pro reprezentované bodové objekty není nutné řešit topologické vztahy. Udáním jejich polohy definujeme jejich nezávislost na jiných body. Pokud však plní body funkci uzlů, tvořících liniové objekty, musíme řešit příslušnost těchto uzlů k jednotlivým liniím.

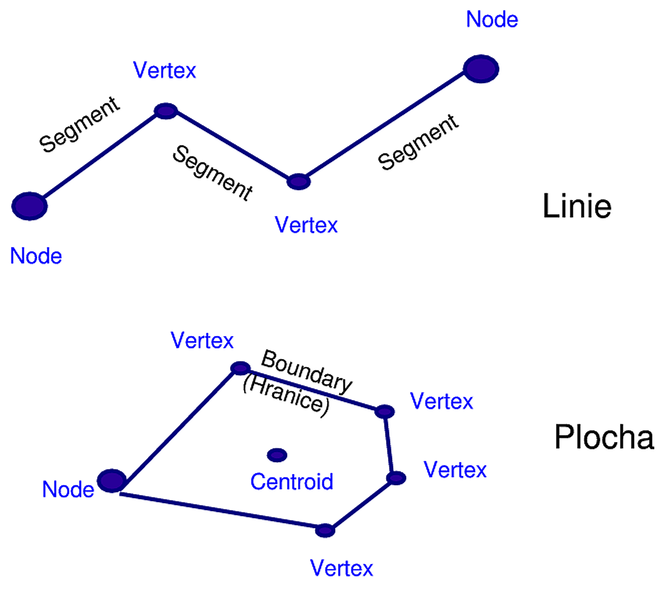
Obrázek 1: Vektorová data (zdroj: http://les-ejk.cz/skoleni/grass/uvod/datove_typy/vektory.html)

Dochází-li ke spojování reprezentovaných liniových objektů, musíme definovat jejich spojitost v průsečících - uzlech. Tento vztah je označován jako spojitost - connectivity.

U reprezentovaných plošných objektů musíme definovat tři druhy topologických vztahů:

• souvislost, spojitost hran, vytvářejících obrys dané plochy v uzlech - connectivity,
• příslušnost hrany k dané ploše, tj. vztah čára - polygon nebo definovat plochy (area definition),
• sousednost ploch - hrany mají udaný směr, takže můžeme určit plochu napravo a nalevo od dané hrany, tj. sousednost ploch - contiguity.

Polohová informace je propojena s uzlem nebo mezilehlým bodem (vertexem) ve formě dvou jeho atributů - souřadnic \(x,y\). Tento způsob lokalizace je používán u všech typů objektů, protože jejich základními stavebními prvky jsou ve všech případech body.

Pro modelování tematické náplně (atributů) existují ve vektorové reprezentaci dva základní přístupy - způsoby organizace databáze: vrstvový a objektový.

Vrstvový přístup organizace databáze s vytvářením pokrytí - coverage je klasický přístup, vycházející z navrhování a vytváření topografických a tématických map v kartografii. Pokrytí (coverage) je sada tématicky příbuzných dat považovaná za jednotku. Zpravidla představuje jednotlivé téma nebo informaci (např. půdy, vodní toky, sídlení jednotky apod.). Pokrytí jsou organizována tak, že obsahují jen geoobjekty se stejnou geometrickou dimenzí a z jedné tématické třídy: bodové pokrytí - měřicí body, kóty, města, studně apod.; liniové pokrytí - vodní toky, silniční síť, síť produktovodů apod.; polygonové pokrytí - parcely, typy půd, vegetační kryt apod.

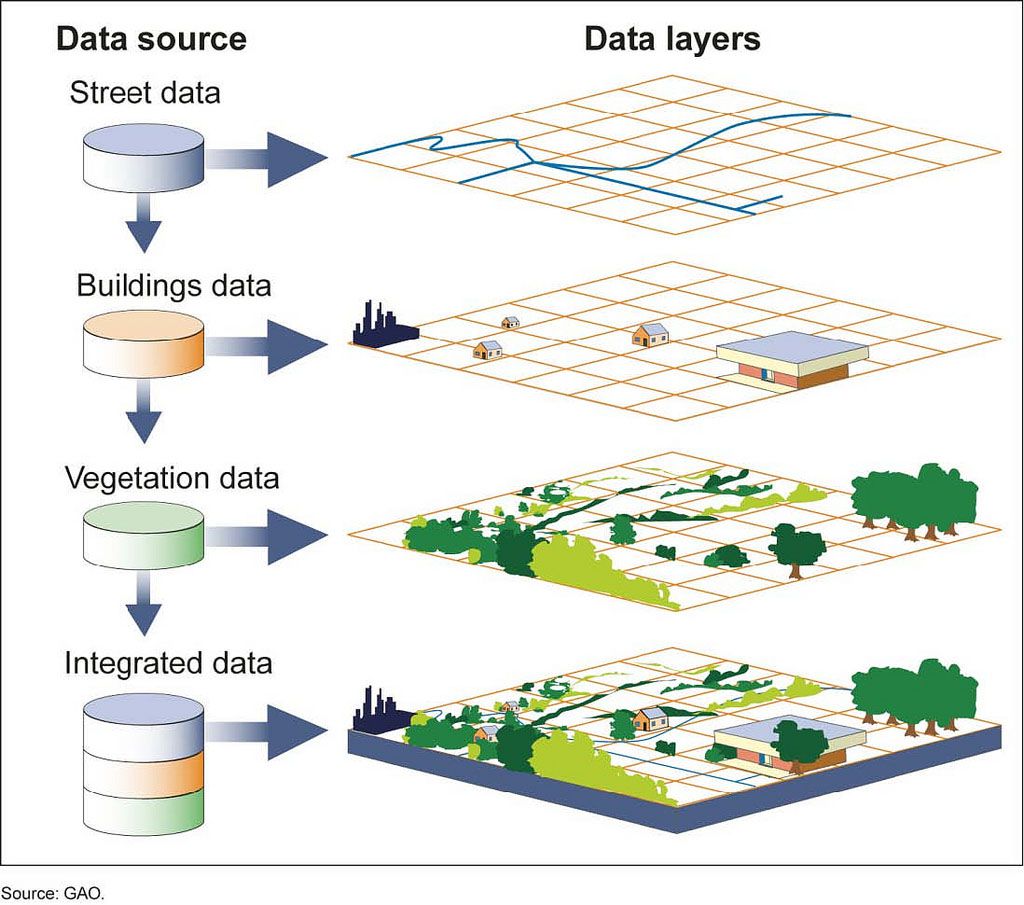
Obrázek 2: Vektorové vrstvy (zdroj: https://www.nationalgeographic.org/encyclopedia/geographic-information-system-gis/)

Výhody vrstvového přístupu spočívají podle některých autorů v:

• možnosti vytváření tématických hierarchií,
• získávání, úpravy a přístup k údajům jsou řešeny specificky pro každou vrstvu,
• velmi rychlé vyhledávání podle atributu.

Nevýhodou je pracnější a pomalejší přístup k objektu z hlediska více (nebo všech) atributů.

Objektový přístup je novější, založený na principech objektového modelování údajů. Jeho základní znaky jsou:

• každý objekt má vlastní geometrii, topologii, tématiku a chování,
• objekty je možné sdružovat do tříd,
• je možné vytvářet hierarchické vztahy mezi objekty,
• atributy a metody se dědí odvozováním pro podtřídu z existující třídy.

Většina použitelných vektorových datových struktur může být v podstatě zařazena do jednoho z následujících “klasických typů”:

• špagetový model,
• topologický model,
• hierarchický model.
  

3.1 Netopologické vektorové struktury

3.1.1 Špagetový model

špagetový model (nespojené vektory) je nejjednodušší typ. Každý geoprvek na mapě je kódován odděleně, bez vytváření vztahů s okolními geoprvky. V podstatě se jedná o přímý přepis klasické mapy čára po čáře do digitální podoby, takže vznikne soubor vektorů a bodů v podobě souřadnic X, Y bez jakékoliv informace o vzájemných vazbách (chybí informace o sousedech), linie se mohou křížit prakticky libovolně. Dnes je považován již za překonaný.

základní charakteristiky špagetového modelu:

• nejsou vyznačeny průsečíky čar ani údaje o logické provázanosti objektů,
• polygony - nezávislé řady souřadnic, společná hranice mezi dvěma polygony je v databázi uložena dvakrát, protože se uložení každé čáry pořizuje samostatně, často jsou souřadnice obou variant společné hranice obyčejně mírně odlišné,
• při vykreslení vytvářejí změť protínajících se čar - podobné “špagetám”,
• nejvíce se používá při digitalizaci map, kdy se data pořizují ruční digitalizací nebo při digitální fotogrammetrické registraci, kdy je zapotřebí reprodukovat původní obrazový dokument,
• používá se především v počítačové grafice, digitální kartografii * špagetový model není vhodný pro prostorové analýzy, protože jakákoliv informace o vztazích mezi objekty, jež je zřejmá při pohledu na původní analogový dokument, se musí odvozovat výpočtem,
• ukládání a prohledávání dat - sekvenční - trvá dlouho.
  

3.2 Topologické vektorové struktury

3.2.1 Topologický model

Základem topologického modelu je záznam linií tvořících mapu ve formě rovinného grafu.

Topologie - obor matematiky, který se zývá popisem a analýzou prostorových vztahů mezi geometrickými objekty. Topologický model vyjadřuje spojení a vazby mezi objekty nezávisle na jejich souřadnicích - jejich topologie zůstává beze změny i když se natahují nebo ohýbají. V GIS je nejvíce používán pro ukládání prostorových dat. Vyžaduje, aby všechny čáry byly spojité a polygony uzavřené.

Hrana začíná a končí v průsečíku s jinou hranou, v uzlovém bodě. Každá individuální hrana má zaznamenané označení a souřadnice svých uzlových bodů (počátku a konce). Dále je u ní zaznamenán identifikátor nebo jméno levého a pravého sousedního polygonu. Tímto způsobem jsou explicitně vyjádřeny prostorové vztahy a mohou být použity v analýzách. Tato topologická informace dovoluje prostorově definovat body, linie i plochy a ukládat je neredundantním způsobem, což je výhodné především pro sousedící polygony, neboť každá hrana je ukládána jenom jednou, tedy i hrana společná. Atributy jsou v samostatných relačních tabulkách; topologie je užitečná pro rychlou analýzu prostorových funkcí bez složitých výpočtů s použitím souřadnic.

Problémem špagetového a topologického modelu je to, že individuální záznamy entit v něm nejsou uspořádány. Chceme-li najít nějakou dílčí hranu v topologické struktuře, musíme sekvenčně, postupně prohledat celý soubor. Chceme-li najít všechny hrany, které definují hranici určitého polygonu, musí být hledání vykonáno tolikrát, kolik hran tuto hranici tvoří.

Někdy je takovéto uspořádání označováno také jako reprezentace NAA (Node-Arc-Area) - uzel - hrana - plocha (např. Worboys, 1995). Základními složkami modelu jsou: zorientovaný oblouk - hrana - arc, průsečík - uzel - node a plocha - polygon - area. Sytémová pravidla jsou takováto:

• Každý zorientovaný oblouk má jeden počáteční a jeden koncový uzel.
• Každý uzel musí být začátkem nebo koncem nejméně jednoho oblouku.
• Každý plocha je ohraničena jedním nebo více zorientovanými oblouky.
• Zorientované oblouky se mohou protínat jen ve svých uzlových bodech.
• Každý zorientovaný oblouk má přesně jednu plochu nalevo a napravo.
• Každá plocha musí být pravou nebo levou plochou (nebo oběma) nejméně jednoho zorientovaného oblouku.

Topologický model tedy v podstatě stojí na třech základních topologických pravidlech:

1. spojitost (conectivity) - popisuje topologii obloukového uzlu pro datový soubor funkcí. Jak již bylo uvedeno dříve, uzly jsou více než jednoduché body. V topologickém datovém modelu jsou uzly průsečíky, kde se setkávají dva nebo více oblouků. V případě topologie obloukového uzlu mají oblouky jak uzel (tj. počáteční uzel) označující, kde oblouk začíná, tak uzel (tj. Koncový uzel) označující, kde oblouk končí (obrázek 4). Kromě toho mezi každou dvojicí uzlů je úsečka, někdy nazývaná spojem, která má své vlastní identifikační číslo a odkazuje jak na uzel, tak na uzel. Na obrázku 4 se oblouky 1, 2 a 3 protínají, protože sdílejí uzel 11. Počítač proto může určit, že je možné pohybovat se po oblouku 1 a obrátit se na oblouk 3, zatímco to není možné přejít z oblouku 1 do oblouku 5, protože nesdílejí společný uzel.

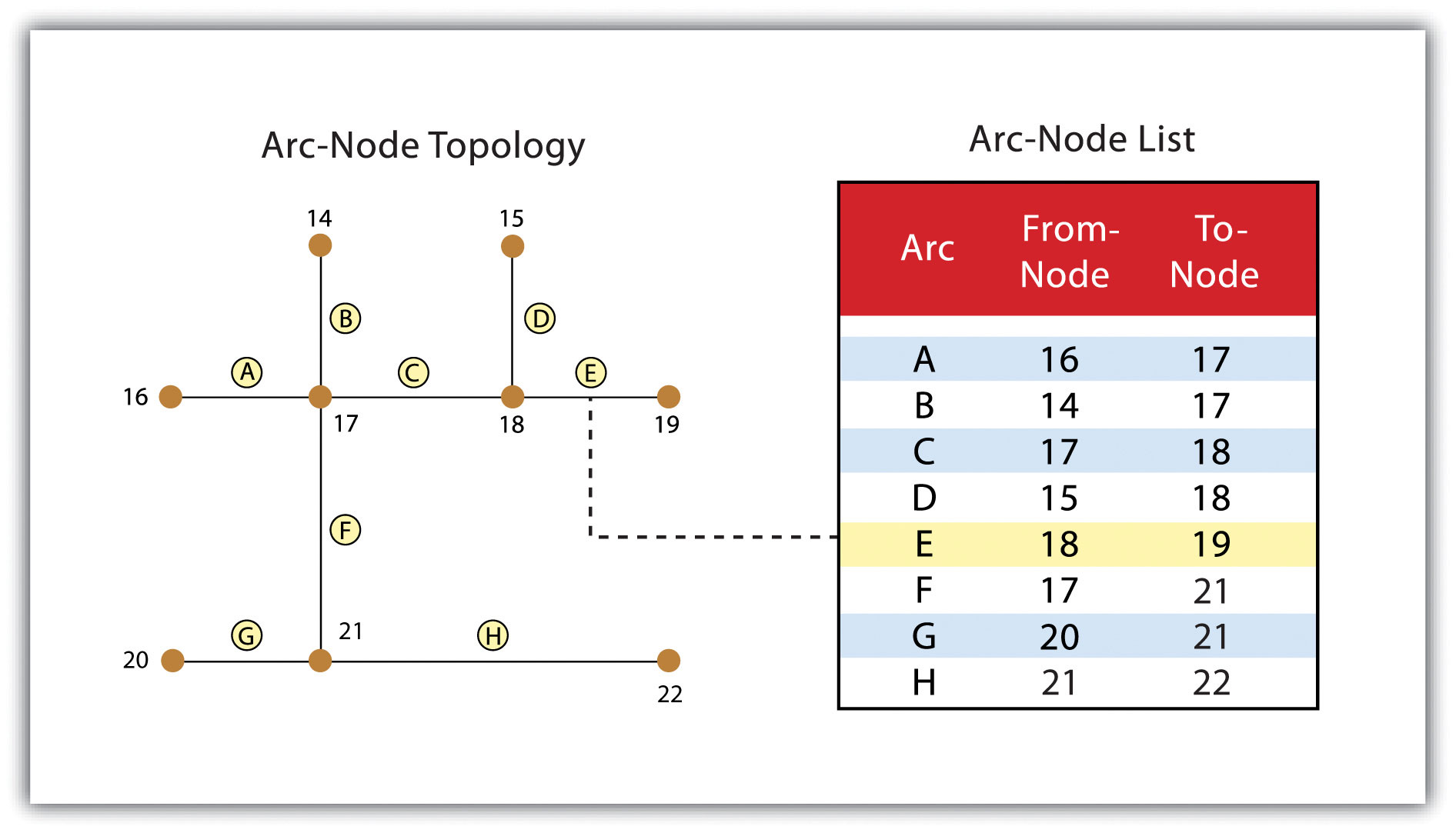
Obrázek 4: Topologie ark - nód (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-data-models-for-gis.html)

2. uzavřenost (linie) - druhým základním topologickým předpisem je definice oblasti. Definice oblasti uvádí, že oblouk, který se připojuje k obklopení oblasti, definuje polygon, také nazývaný topologie polygonového oblouku. V případě topologie mnohoúhelníkového oblouku se oblouky používají ke konstrukci polygonů a každý oblouk je uložen pouze jednou (obrázek 5). To má za následek snížení množství uložených dat a zajišťuje, že sousední polygonové hranice se nepřekrývají. Na obrázku 5 je vidět, že polygon F je tvořen oblouky 8, 9 a 10.

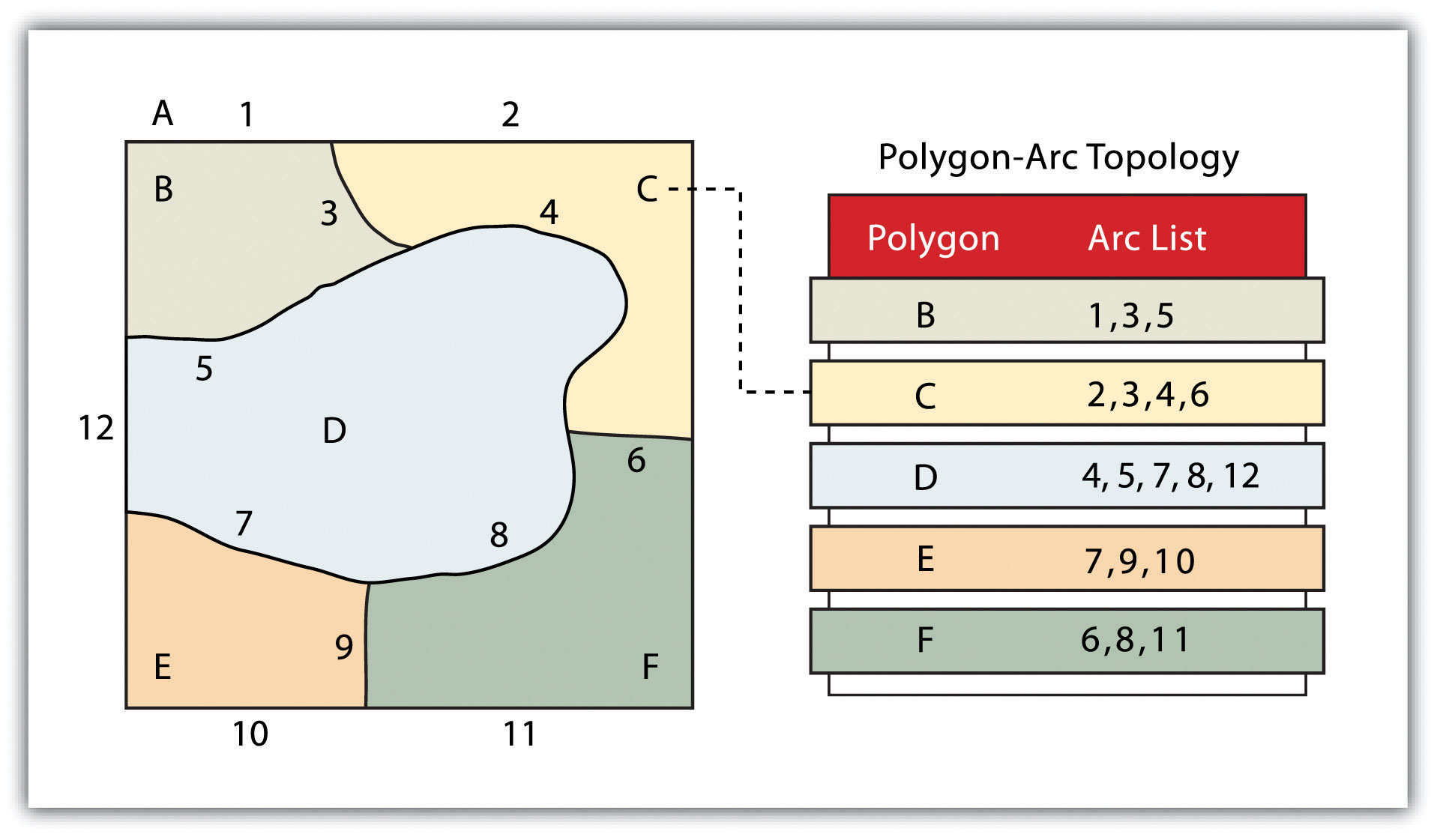
Obrázek 5: Topologie ark - polygon (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-data-models-for-gis.html)

3. sousednost (contiguity) - je založena na konceptu, že polygony, které sdílejí hranici, jsou považovány za sousedící. Konkrétně topologie mnohoúhelníku vyžaduje, aby všechny oblouky v mnohoúhelníku měly směr (z uzlu a do uzlu), což umožňuje určit informaci o sousednosti (obrázek 6). Polygony, které sdílejí oblouk, se považují za sousední nebo sousedící, a proto lze definovat „levou“ a „pravou“ stranu každého oblouku. Tato informace o levém a pravém mnohoúhelníku je explicitně uložena v atributové informaci topologického datového modelu. „Vesmírný mnohoúhelník“ je nezbytnou součástí topologie mnohoúhelníku, která představuje vnější oblast umístěnou mimo studijní oblast. Obrázek 6 ukazuje, že oblouk 6 je nalevo spojen mnohoúhelníkem B a vpravo mnohoúhelníkem C. Mnohoúhelník A, mnohoúhelník vesmíru, je nalevo od oblouků 1, 2 a 3.

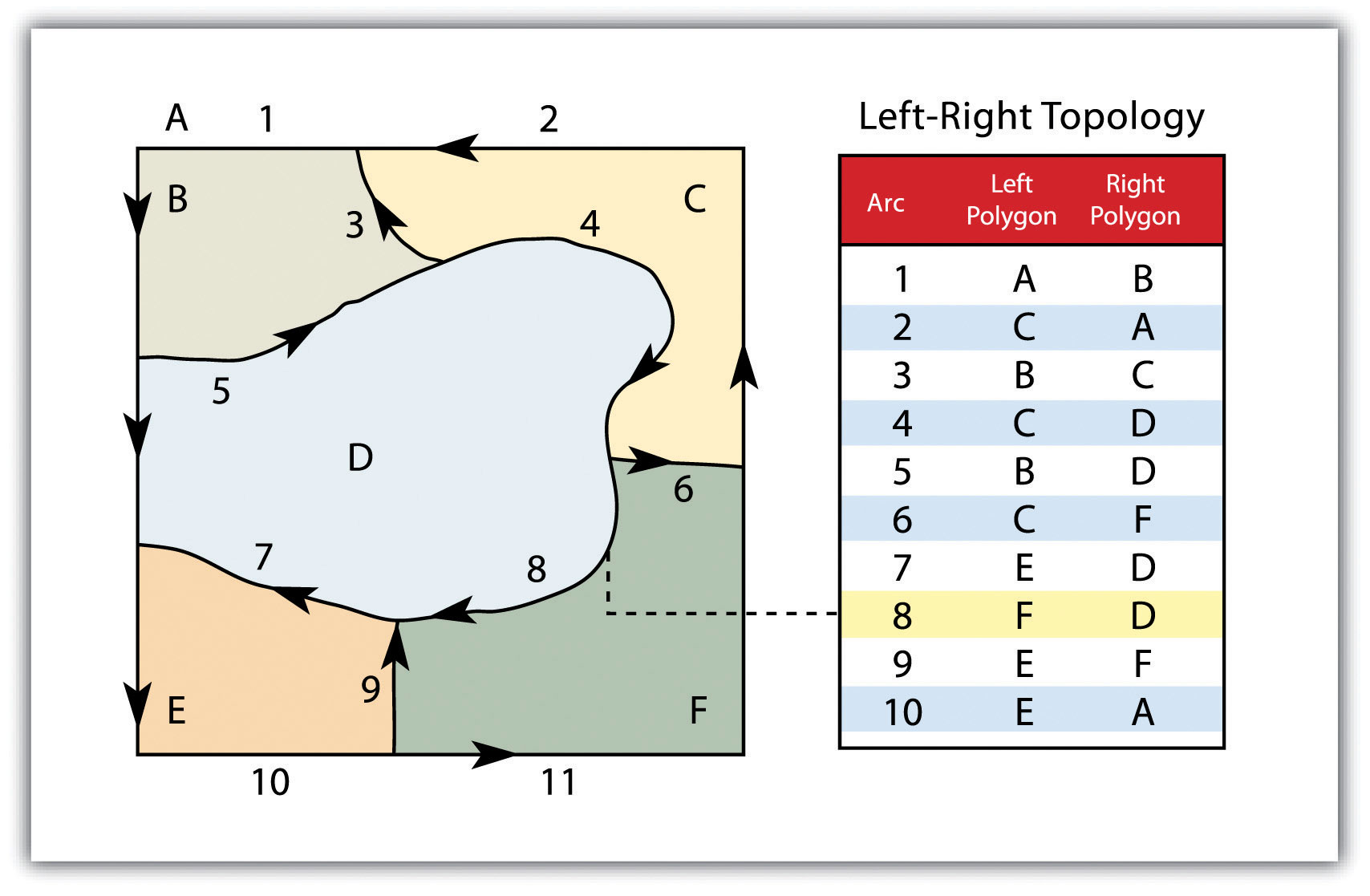
Obrázek 6: Polygonová topologie (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-data-models-for-gis.html)

Topologie umožňuje počítači rychle určit a analyzovat prostorové vztahy všech jeho zahrnutých funkcí. Kromě toho jsou topologické informace důležité i proto, že umožňují účinnou detekci chyb v rámci vektorového datového souboru. V případě polygonových rysů porušují otevřené nebo neuzavřené polygony, které se vyskytují, když se oblouk zcela sám nevrací, a neznačené polygony, které se objevují, když oblast neobsahuje žádné atributy, porušují pravidla topologie polygonového oblouku. Další topologickou chybou nalezenou u polygonálních funkcí je pramen. K úlomkům dochází, když se společná hranice dvou polygonů přesně nesplňuje (obrázek 7).

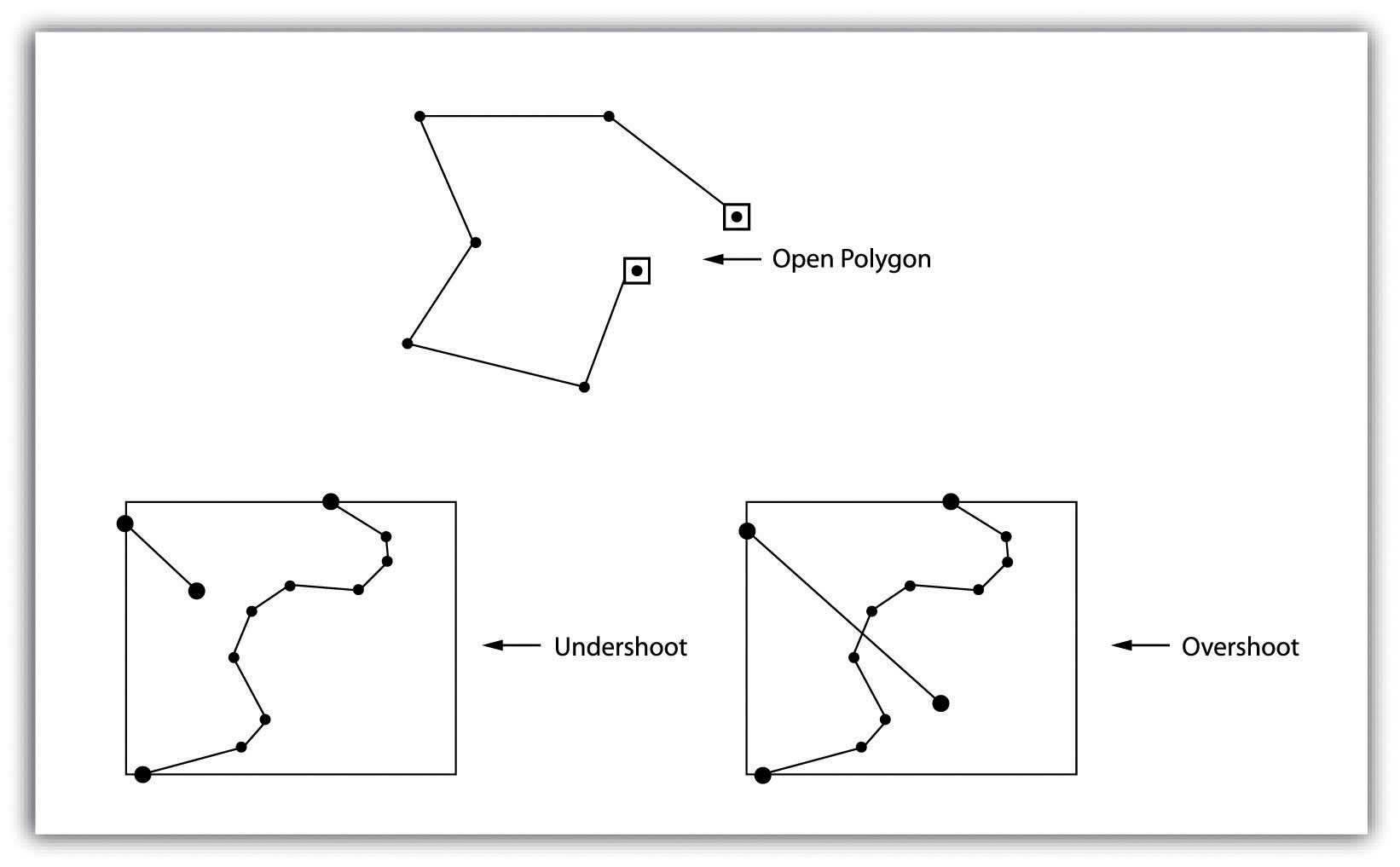
Obrázek 7: Běžné topologické chyby vektorových dat (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-data-models-for-gis.html)

Mnoho typů prostorové analýzy vyžaduje stupeň organizace nabízený topologicky explicitními datovými modely. Zejména síťová analýza (např. nalezení nejlepší trasy z jednoho místa na druhé) a měření (např. nalezení délky úseku řeky) silně závisí na konceptu uzlů a hran, a tyto informace používá společně s informacemi o atributech, pro výpočet vzdáleností, nejkratších tras, nejrychlejších tras atd. Topologie také umožňuje sofistikovanou analýzu sousedství, jako je určení sousedství, shlukování, nejbližší sousedé atd.

Takovýto topologický model lze velmi pohodlně reprezentovat v relačním databázovém modelu.

3.2.2 Další vylepšení topologického modelu

Double Connected Edge List

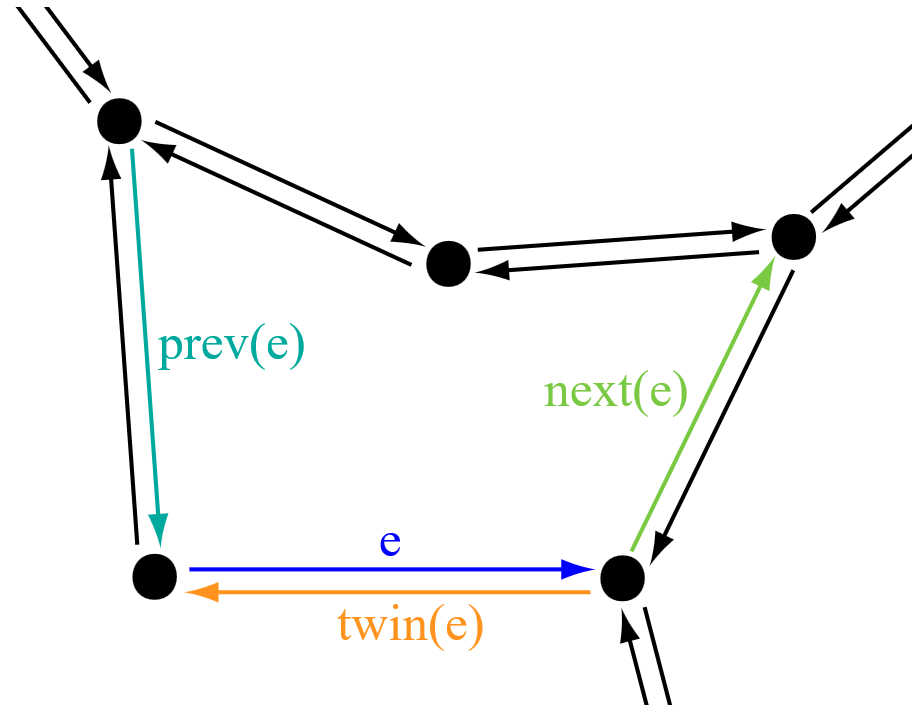
Jako vylepšení NAA reprezentace uvádí Worboys (1995) tzv. DCEL (Double Connected Edge List) - seznam dvojitě propojených hran, který vylepšuje možnosti prohledávání struktury uvedením předcházející a následující hrany u každé popisované hrany.

DCEL je více než jen dvojitě propojený seznam hran. V obecném případě obsahuje DCEL záznam pro každou hranu, vrchol a plochu dělení; každý záznam může obsahovat další informace, například tvář může obsahovat název oblasti. Každá hrana obvykle ohraničuje dvě plochy, a proto je vhodné považovat každou hranu za dvě „poloviční hrany“ (které jsou na obrázku 8 vpravo znázorněny dvěma hranami v opačných směrech, mezi dvěma vrcholy); každá “poloviční hrana” je „spojena“ s jednou plochou a má tedy na tuto plochu ukazatel. Všechny “poloviční hrany” spojené s plochou jsou orientovány ve směru nebo proti směru hodinových ručiček. Například na obrázku vpravo jsou všechny “půlhrany” přidružené ke střední ploše (tj. “vnitřní” půlhrany) proti směru hodinových ručiček. Poloviční hrana má ukazatel na další půlhranu a předchozí půlhranu stejné plochy. Abychom dosáhli druhé plochy, můžeme se posunout k dvojici půlhran a pak projít další plochou; každá půlhrana má také ukazatel na svůj počáteční vrchol (cílový vrchol lze získat dotazováním na původ jeho dvojčete nebo další půlhrany).

Obrázek 8: DCEL (zdroj: https://wikivisually.com/wiki/Doubly_connected_edge_list)

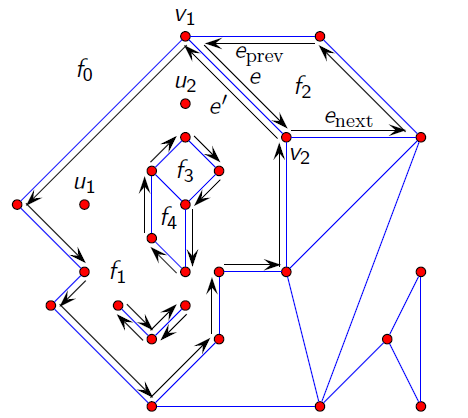
DCEL je jednou z kombinatorických datových struktur, které jsou označovány jako “halfedge data-structures”. Ukládá vztahy incidence mezi 0-rozměrnými (vrcholy), 1-rozměrnými (hrany) i 2-rozměrnými (plochy) objekty.

DCEL strukturu tedy tvoří (viz obrázek 9):

• vertex - incidentní půlhrana směřující do tohoto bodu
• půlhrana (halfedge)
  • protější půlhrana
  • předcházející půlhrana v hranici objektu
  • následující půlhrana v hranici objektu
  • cílový vertex půlhrany
  • incidentní plocha
• plocha - incidentní půlhrana hranice plochy
• propojená součást hranice
  • kruhové řetězce půlhran kolem ploch

Windged Edge

Dalším zlepšením je reprezentace ve formě tzv. okřídlené hrany - windged edge, ve které jsou popsány všechny možné informace o souvislostech mezi uzly, hranami a plochami.

V reprezentaci okřídlené hrany (windged edge) je za základní prostorový objekt považována hrana (edge). S každou hranou je jsou sdruženy její dvě příslušné plochy: p-face, n-face a dva vertexy: p-vertex, n-vertex. S každou hranou jsou také svázány další čtyři hrany, tak jak naznačuje obrázek 10: nc-edge (hrana následující ve směru hodinových ručiček), pc-edge (předcházející hrana ve směru hodinových ručiček), na-edge (hrana následující proti směru hodinových ručiček) a pa-edge (hrana předcházející proti směru hodinových ručiček). Tato reprezentace poskytuje kompletní charakteristiku topologie ve smyslu incidence, sousednosti a uspořádání hran, vertexů a ploch.

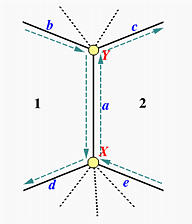
3.2.3 Hierarchický model

Hierarchický vektorový model překonává nevýhodu jednodušších vektorových modelů a struktur při vyhledávání entit tím, že zvlášť ukládá údaje o bodech, uzlech, liniích - hranách a plochách - polygonech v logické hierarchické struktuře. Polygony jsou definovány prostřednictvím linií a ty jsou reprezentovány jako řetězce bodů, tzn. je možné explicitním způsobem vybudovat model propojení ve kterém závisí jeden typ objektu na druhém (viz obrázek 11). Takovéto propojení poskytuje přímý vyhledávací mechanismus.

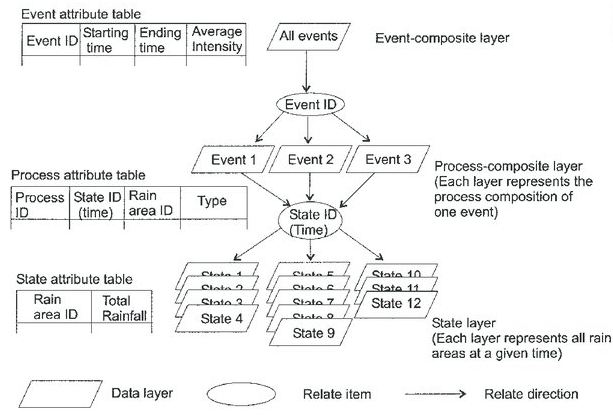
Obrázek 11: Hierarchický datový model (zdroj: Yuan, 2001)

Fyzická separace jednotlivých tříd elementů umožňuje nižší nároky na paměťový prostor, zrychlení většiny operací. Naopak, toto fyzické oddělení vyžaduje ukládat složité struktury vyhledávačů, identifikátorů. Tyto nedatové elementy přidávají výrazný objem potřebného paměťového prostoru a zároveň představují potenciální problém při zabezpečení a udržení integrity údajů.

3.3 Zhodnocení vektorové datové reprezentace

Výhody

• lze pracovat s jednotlivými objekty jako se samostatnými celky;
• menší náročnost na paměť;
• dobrá reprezentace jevové struktury dat;
• vysoká geometrická přesnost
• kvalitní grafika, přesné kreslení, znázornění blízké mapám;
• jednoduché vyhledávání, úpravy a generalizace objektů a jejich atributů.
  

Nevýhody

• výpočtová náročnost (problémy při náročných analytických operacích);
• komplikovanost datové struktury;
• složitější odpovědi na polohové dotazy;
• obtížná tvorba překryvů vektorových vrstev (overlay)
• problémy při modelování a simulaci jevů.