Kapitola 2 Abstrakce a modelování v GIS

Lidé žijí v konkrétním prostředí, které je obklopuje a které svým uspořádáním a svými vlastnostmi do značné míry předurčuje způsob jejich života. Například jinak žijí lidé v Rusku a jinak v Austrálii. Působení je ale vzájemné – i člověk více či méně na toto prostředí působí, mění (modifikuje) jeho složky, ovlivňuje jeho vývoj. Například těží nerostné suroviny, staví města, znečišťuje prostředí.

V tom nejobecnějším pojetí budeme tomuto prostředí říkat reálný svět. V průběhu své historie člověk rozvinul celou řadu vědních disciplín, zabývajících se jeho popisem a studiem. Namátkou můžeme jmenovat geografii, geodézii, kartografii, geologii, geoinformatiku. Důvodem jejich vzniku byla (a stále je) snaha co nejlépe porozumět objektům, jevům a událostem v něm se vyskytujícím a procesům v něm probíhajícím. O reálném světě lze říct, že existuje zcela nezávisle na našem vědomí, na našich subjektivních vjemech, na našem poznání. Z pohledu tohoto textu budeme reálný svět považovat za poznatelný jen částečně. Úplné poznání reálného světa je technicky, ale i ekonomicky neproveditelné.

Příklad (Rapant, 2014). Asi se nám nikdy nepodaří prozkoumat všechny hvězdy naší Galaxie, natož všechna zákoutí našeho Vesmíru. Ale koneckonců není třeba ani uvažovat tyto extrémní případy. Ani nitro naší planety Země není pro nás zcela poznatelné. Ačkoliv penzum našich znalostí roste, přesto pro nás bude značná část informací z technických důvodů stále nedosažitelná.

Při poznávání reálného světa se v geoinformatice omezujeme zpravidla jen na tu jeho část, v níž aktivně žijeme, kterou využíváme k uspokojení svých potřeb, kterou spravujeme a kterou různým způsobem ovlivňujeme.

Nicméně nic nám nebrání poznatky geoinformatiky a na nich založené geoinformační technologie používat v mnohem širším kontextu. Dnes se rozvíjejí aplikace geoinformačních technologií například pro Mars (vytváří se geografický informační systém, shrnující všechny doposud získané údaje o něm (např. viz Google Earth); zpracovává se koncept marsovského družicového navigačního systému; běžně se provádí systematický dálkový průzkum Marsu prostřednictvím umělých družic Marsu – viz projekty jako Mars Global Surveyor, Mars Odyssey, Mars Express, Mars Reconnaissance Orbiter). Obdobné systémy se realizují například i pro Měsíc a další tělesa sluneční soustavy.

2.1 Náhledy na reálný svět

S ohledem na to, co můžeme v reálném světě pozorovat, se na reálný svět můžeme dívat různými způsoby:

• reálný svět může být vnímán jako prostor, v němž se nachází množina diskrétních objektů reálného světa rozložených v prostoru, popsaných hodnotami jejich vlastností (tzv. objektový náhled),
• reálný svět může být vnímán jako prostor, v němž existuje množina jevů popisujících rozložení hodnot vlastností reálného světa v prostoru (tzv. jevový náhled),
• reálný svět může být vnímán jako prostor, v němž dochází k událostem popisujícím změny uspořádání a vlastností reálného světa, které jsou prostorově i časově ohraničené (tzv. událostní náhled),
• reálný svět může být vnímán i jako prostor, v němž probíhá a který utváří množina procesů (tzv. procesní náhled).

Každý z těchto náhledů je vhodný pro studium jiných aspektů reálného světa. Je však nesporné, že tyto náhledy nejsou navzájem zcela nezávislé. Každý z nich sice zahrnuje jen specifickou část aspektů reálného věta, avšak dochází přitom mezi nimi i k určitým překryvům. Pro komplexní porozumění reálnému světu proto musíme tyto čtyři náhledy kombinovat.

2.1.1 Objektový náhled

V rámci objektového náhledu reálný svět popisujeme prostřednictvím tzv. objektů. Pojem objekt (angl. object) je na nejobecnější úrovni definován ve filozofii. Zde se nejčastěji uvádí definice (Merriam-Webster Online Dictionary):

Objekt je cokoliv materiální povahy, co může být vnímáno smysly.

Tato definice jsou příliš obecná, pro potřeby dalšího výkladu (tj. z pohledu geoinformatiky) je nezbytné význam pojmu objekt vymezit poněkud úžeji. Proto si zavedeme pojem objekt reálného světa (angl. real world object), který budeme definovat takto (Rapant 2006):

Objekt reálného světa je jakákoliv odlišitelná, vymezitelná (prostorově, časově, tematicky, funkčně i vztahově) a jednoznačně identifikovatelná část reálného světa.

Každý objekt reálného světa je možné popsat šesticí (upraveno podle Laurini, Thompson, 1994):

\([o,a,s,r,f,t]\),

kde \(o\) reprezentuje daný objekt (object), \(a\) reprezentuje sadu neprostorových vlastností (atributů) popisujících objekt (attributes), \(s\) reprezentuje sadu prostorových vlastností objektu (spatial attributes), \(r\) reprezentuje vztahy, do nichž objekt vstupuje (relationships), \(f\) reprezentuje akce (činnosti - functions), které lze s objektem provádět a \(t\) reprezentuje čas (time).

Z pohledu objektového náhledu má reálný svět poměrně složitou vnitřní strukturu, kterou nejčastěji popisujeme jako hierarchickou. Na nejnižší úrovni můžeme hovořit o základních stavebních kamenech představovaných subatomovými částicemi (dnes se na nejnižší úrovni nacházejí tzv. kvarky), na nejvyšší úrovni stojí prozatím náš Vesmír. Z pohledu geoinformatiky nás ale bude zajímat jen určitý výsek této hierarchické struktury, začínající objekty reálného světa (na nejnižší hierarchické úrovni) a končící planetou Zemí a jejím bezprostředním okolím (na nejvyšší hierarchické úrovni. Takto vymezený výsek hierarchie popisuje tu část reálného světa, v níž se člověk v současné době běžně (nebo i méně běžně) pohybuje (Rapant 2006).

Reálný svět se pro nás bude skládat z konkrétních objektů reálného světa a jejich seskupení (tzv. agregací (angl. agregation), tj. složitějších objektů, vzniklých složením z jednodušších objektů – viz dále).

Objekty reálného světa můžeme dělit na fyzické a abstraktní. Příkladem fyzického objektu reálného světa může být řeka Vltava, Kulturní dům Metropol v Českých Budějovicích, pohoří Šumava, planeta Země apod., tj. jakákoliv fyzicky existující část reálného světa. Příkladem abstraktního objektu reálného světa může být jednotka územně správního členění státu (Jihočeský kraj), konkrétní sčítací obvod nebo konkrétní volební obvod apod. Jsou to tedy jednotky, které v reálném světě fyzicky neexistují, člověk si je vytváří uměle.

Na základě shodných vlastností mohou být objekty reálného světa sdružovány do tzv. tříd objektů reálného světa (Rapant, 2006):

Třída objektů reálného světa je tvořena skupinou objektů reálného světa se společnými znaky (vlastnostmi).

Příkladem může být třída listnatý strom. Do této třídy patří všechny objekty reálného světa, představované listnatými stromy, tj. všechny lípy, javory, kaštany … Jejich společnými vlastnostmi mohou být například botanický název, poloha, stáří, výška a průměr koruny.

Objekty reálného světa pro nás budou představovat základní stavební kameny reálného světa. Nicméně v běžné praxi obvykle pracujeme s komplexnějšími jednotkami, tvořenými logickými i fyzickými seskupeními (agregacemi) jednodušších objektů. Zda budeme daný objekt reálného světa vnímat jako agregaci jednodušších objektů, nebo jako objekt samotný, bude záviset na úrovni rozlišení, na níž budeme reálný svět studovat.

Příklad: Město je komplexní jednotka, která je tvořena jednotlivými budovami, chodníky, silnicemi, stromy, trávníky apod., představujícími jednotlivé objekty reálného světa.

Budeme-li o městě hovořit z pohledu celé republiky, obvykle ho budeme vnímat jako jednoduchý objekt reálného světa.

Naopak například na úrovni rozlišení uliční sítě již můžeme město vnímat jako agregaci jednodušších objektů, jako jsou dříve zmíněné budovy, chodníky apod.

Při objektovém popisu reálného světa nejprve identifikujeme jednotlivé třídy objektů reálného světa, které popíšeme jejich vlastnostmi, a po té identifikujeme jednotlivé objekty reálného světa, které pak popisujeme hodnotami příslušných vlastností. Každá vlastnost objektu reálného světa má zpravidla přiřazenu jedinou hodnotu platnou pro celý objekt.

Příklad (Rapant, 2014): Objekty patřící do třídy listnatý strom mají například následující vlastnosti:

• evidenční číslo,
• botanický název,
• poloha X,
• poloha Y,
• stáří,
• výška koruny,
• průměr koruny.

Každý objekt reálného světa – listnatý strom – je popsaný konkrétními hodnotami těchto vlastností, např.:

• 125/92,
• lípa obecná,
• 100,
• 150,
• 120,
• 25,

2.1.2 Jevový náhled

Pojem jev (angl. phenomenon) můžeme definovat na nejobecnější úrovni (ve filosofii) například takto (Enciclopaedia Britannica):

Jev je obecně jakýkoliv vnímaný nebo pozorovaný objekt, fakt nebo výskyt.

Z pohledu tohoto textu si však význam pojmu jev poněkud omezíme (Rapant, 2006):

Jev reálného světa je jakákoliv odlišitelná, vymezitelná (prostorově i časově) a jednoznačně identifikovatelná vlastnost reálného světa, jejíž hodnoty jsou definovány zpravidla v každém bodě studovaného prostoru a případně i časového intervalu.

Na rozdíl od objektu reálného světa, u kterého klademe důraz na to, že se jedná o prostorově vymezitelnou část reálného světa, kterou můžeme popsat jejími vlastnostmi (a co je podstatné, každý objekt má pro celý prostor, který zaujímá, zpravidla přiřazenu jedinou hodnotu dané vlastnosti), u jevu klademe naopak důraz na to, že se jedná o vlastnost, u níž studujeme časové a prostorové rozložení jejích hodnot popisujících různá místa v tomto prostoru.

Příklad (Rapant, 2014): Objektu typu parcela může být přiřazena jediná hodnota nadmořské výška (např. průměrná hodnota), i když je jasné, že parcela nacházející se na strmém svahu má v různých místech různou nadmořskou výšku. Naproti tomu pokud budeme sledovat přímo nadmořskou výšku v zadané oblasti, budeme si zpravidla definovat síť bodů, v nichž nadmořskou výšku zaměříme, ale nebudeme přitom mít žádnou informaci o tom, na které parcele které body leží. Tuto informaci však můžeme získat následnou analýzou.

Každý jev reálného světa je proto možné popsat pěticí (Laurini, Thompson, 1994):

\([p,{v,(x,y,z)},b,t]\),

kde \(p\) reprezentuje vlastnost prostoru, \(b\) reprezentuje prostorové vymezení oblasti, v níž jev studujeme (hranici oblasti; angl. boundary) a \(t\) reprezentuje čas (time). Množina \({v, (x, y, z)}\) reprezentuje uspořádané dvojice hodnota-poloha, popisující rozložení hodnot vlastnosti v prostoru, kde \(v\) reprezentuje konkrétní hodnotu vlastnosti a \((x, y, z)\) reprezentuje polohu v prostoru, k níž se tato hodnota vztahuje.

V případě jevového náhledu se tedy na svět díváme jako na sadu jevů popsaných daným rozložením hodnot různých vlastností reálného světa v prostoru (a případně i čase).

Jevy reálného světa můžeme dělit podle různých kritérií (Rapant, 2006).

Nejjednodušší je dělení jevů dle povahy hodnotové domény vlastností na:

• kvalitativní (například využití území),
• kvantitativní (například nadmořská výška).

Jiným kritériem může být spojitost prostoru, resp. hodnotové domény, na:

• kontinuální (například nadmořská výška),
• diskrétní (například osídlení).

Další dělení se může odvíjet od proměnlivosti v čase na:

• statické (například nadmořská výška),
• dynamické (například meteorologické jevy).

Jiné členění může být podle počtu prostorových dimenzí studovaného jevu (Rapant, 2006):

• 0-rozměrné (bodové) - např. koncentrace znečišťujících látek v daném bodě,
• 1-rozměrné (liniové) - např. rozložení koncentrací znečišťujících látek podél vodního toku,
• 2-rozměrné (plošné rovinné) - např. land use, geologická stavba apod.,
• 2.5-rozměrné (plošné prostorové) - tzv. povrchy - např. nadmořská výška nebo rozložení koncentrací znečišťujících látek v půdách na daném území,
• 3-rozměrné (objemové) - např. rozložení vlhkosti v troposféře nebo rozložení koncentrací rudních minerálů v ložisku.

doplnit obrázek!!!

2.1.3 Událostní náhled

Zatímco při studiu objektů a jevů můžeme zanedbat čas a považovat je tady za čistě prostorové (statické), v případě událostí (angl. event) je zahrnutí času do našich úvah nezbytné. Vyplývá to už ze samotné definice události. Podívejme se na některou z obecných definic:

Událost je něco, co se vyskytuje na určitém místě v průběhu určitého časového intervalu (Dictionary.com).

nebo

Událost je základní entita pozorované fyzikální reality, reprezentovaná bodem určeným třemi souřadnicemi místa a jednou souřadnicí času v časoprostorovém kontinuu, postulovaná teorií relativity (Merriam-Webster Online Dictionary).

Tyto dvě definice se liší v jedné zásadní věci: zatímco první připouští, že událost má rozměr, tj. zaujímá určitý prostor a čas, druhá pojímá událost jako bezrozměrnou. Druhá definice je úzce svázána s teorií relativity. Z našeho pohledu je vhodnější definice první, kterou si mírně modifikujeme do tvaru (Rapant, 2014):

Událost je něco, co se stane v přesně vymezeném prostoru i čase.

V této definici je důležité slovo „stane“. Znamená to, že událost se svojí povahou liší od objektu: objekt zaujímá určitý prostor, událost se v určitém prostoru vyskytne (angl. occure).

Prostorově se může událost vztahovat k bodu – například výbuch nálože, k linii – například znečištění řeky, nebo k ploše – například povodeň. Z časového pohledu může být mžiková (třeba výstřel), nebo může trvat určitou dobu (například povodeň: dnes běžně hovoříme o povodni na Moravě v roce 1997 a bereme ji jako jednorázovou, prakticky mžikovou. Ve skutečnosti ale probíhala skoro čtrnáct dní – 5.-16.7.1997).

2.1.4 Procesní náhled

Vedle objektů, jevů a událostí můžeme v reálném světě popisovat i procesy, které vnášejí do tohoto světa dynamiku, ovlivňují (mění) jeho objekty i jevy, ale ovlivňují i jiné procesy a generují události.

Termín proces (angl. process) je na nejobecnější (tedy filozofické) úrovni definován takto (Merriam-Webster Online Dictionary):

Proces je přirozený jev vyznačující se postupnými změnami vedoucími ke konkrétnímu výsledku.

nebo (tamtéž):

Proces je přirozená průběžná aktivita nebo funkce.

anebo (tamtéž):

Proces je posloupnost akcí nebo operací vedoucích k finálnímu výsledku.

Z pohledu geoinformatiky je nezbytné opět zavést poněkud zúžený výklad (Rapant, 2006):

Proces reálného světa je jakákoliv aktivita nebo posloupnost aktivit (ať už přirozená nebo umělá), ovlivňujících objekty a jevy reálného světa, případně i jiné procesy reálného světa a generující události.

Vzhledem k tomu, že bereme v úvahu i prostorové aspekty, budeme v tomto případě pod pojmem proces uvažovat i prostorový proces (angl. spatial process), i když to nebudeme většinou explicitně uvádět.

Můžeme proto rozlišovat (Rapant, 2006):

• neprostorový proces – mění/ovlivňuje pouze hodnoty negeometrických vlastností objektů (bez přímé vazby na jejich polohu v prostoru), nemění jejich prostorové uspořádání a také na něm nezávisí; příkladem může být proces „změna vlastnictví parcely“, který způsobí změnu hodnoty vlastnosti „vlastník parcely“, ale její výměra, tvar, sousedství apod. zůstane nezměněn,
• prostorový proces – mění/ovlivňuje prostorové uspořádání objektů a případně i hodnoty jejich negeometrických vlastností, resp. mění hodnoty vlastností (jevů) v závislosti na poloze; příkladem může být proces „rozdělení parcely na dvě části“ (dojde ke změně výměry, tvaru, sousedství), „eroze půdy“ (průběžně se mění tvar reliéfu terénu) apod.

Prostorový proces se skládá ze dvou základních komponent: prostorové struktury (nebo vzoru; angl. spatial structure nebo spatial pattern) a prostorového pohybu (angl. spatial movement), který způsobuje změny (transformace) prostorové struktury (Pang, Shi 2002). Vstupem do systému může být např. energie, hmota, obyvatelstvo apod. Stejně různorodý může být i výstup. Schematicky jsou vztahy mezi komponentami prostorového procesu zachyceny na obrázku 1 a blíže vysvětleny v následujícím příkladu.

Příklad (Rapant, 2014): Mějme prostorový proces – migrace obyvatelstva. Prostorovou strukturu reprezentují sídla a továrny a dále síť komunikací mezi nimi, prostorový pohyb je reprezentován pohybem obyvatel mezi sídly a továrnami po komunikacích. Vstupem může být například počáteční rozložení obyvatelstva ve studovaném prostoru (a potažmo v sídlech) a informace ovlivňující chování obyvatelstva (např. aktuální cena benzínu, ceny nemovitostí a náklady na pronájmy bytů resp. výstavbu rodinných domů v různých částech města, předpokládaný vývoj pracovních míst ve městě apod.), výstupem může být změna rozložení obyvatelstva po určité době.

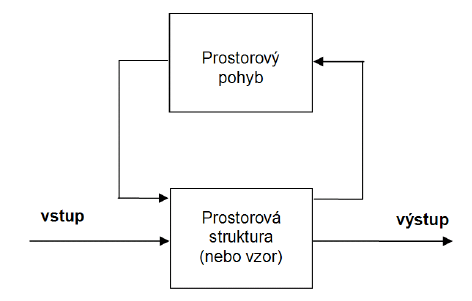
Obrázek 1: Komponenty prostorového procesu a jejich vzájemný vztah (zdroj: Rapant, 2014)

I procesy reálného světa je možné dělit dle různých kritérií, např. na:

• kvalitativní (například změna využití půdy) a kvantitativní (například šíření znečišťujících látek ve vodě),
• kontinuální (například eroze půdy) a diskrétní (například zemětřesení), apod.

Procesy lze v dnešních geoinformačních systémech modelovat jen v omezené míře. Daleko častěji dochází k integraci geoinformačních systémů s účelovými modely jednotlivých procesů. Geoinformační systém slouží pro shromažďování a přípravu dat pro model (tzv. preprocessing) a pro analýzu a vizualizaci výsledků modelování (tzv. postprocessing).

2.2 Modelování v geoinformatice

Reálný svět je reprezentován prostředím, které nás obklopuje. Naopak modelový svět je svět „umělý“, svět, který si vytváříme na základě našich pozorování reálného světa. V prvním kroku si ho vytváříme čistě v našich hlavách – vytváříme si tzv. mentální model, který reprezentuje reálný svět, vztahy mezi jeho objekty, jevy, událostmi a procesy a naše intuitivní představy o možném dalším postupu a jeho následcích. Ten se pak snažíme přetransformovat do počítačového prostředí tak, aby vytvořený počítačový model co nejlépe vystihoval pozorovanou realitu v kontextu úloh, které chceme s použitím počítačového modelu řešit.

Každý model vytváříme vždy v kontextu jeho zamýšleného užití. Proto je každý model určitým zjednodušením reality – zachycujeme v něm jen ty aspekty reálného světa, které jsou v kontextu zamýšleného užití podstatné, ostatní zanedbáváme jako nepodstatné.

Příklad (Rapant, 2014): Máme za úkol vytvořit informační systém pro evidenci inventáře vlastněného organizací. Když se podíváme po místnosti, v které se při přednášce nacházíme (náš reálný svět), ze všeho, co zde vidíme (osoby, stoly, židle, katedru, datový projektor, počítač, světla, tabuli, okna, dveře, křídu, umyvadlo, umyvadlovou baterii, houbu, hadr atd.) má smysl do informačního systému zahrnout pouze ty objekty, které mají inventární číslo. Z vyjmenovaných jsou to nejspíše jen: stoly, židle, katedra, datový projektor, počítač, tabule. Vše ostatní je buďto pevně spojeno s budovou a nemá to samostatné inventární číslo (okna, dveře, světla, umyvadlo …), nebo je cena tak nízká, že nemá smysl dané věci evidovat, jedná se spíš o spotřební materiál (křída, houba, hadr). Náš modelový svět, a tedy náš mentální a nakonec i počítačový model se smrskne jen na stoly, židle, katedru, datový projektor, tabuli. V kontextu dané úlohy je tento výběr objektů dostačující. Zcela jsme samozřejmě zanedbali jevy, události a procesy, které jsou v daném kontextu irelevantní.

Můžeme tedy shrnout, že modelový svět je tvořen řadou modelů (zatím jsme zmínili jen dva – mentální a počítačový), je zjednodušený a kontextově závislý.

2.2.1 Modelování objektů reálného světa v geoinformatice

Jak již bylo uvedeno v 1. kapitole, geoinformatika je věda, zabývající se studiem vlastností, chování a vzájemných interakcí prostorových objektů, jevů, událostí a procesů prostřednictvím jejich digitálních modelů a s využitím informačních a geoinformačních technologií. Geoinformatika tedy pracuje s modely reálného světa. Ty jsou dnes založeny nejčastěji na prvních dvou náhledech na reálný svět – na objektovém a jevovém.

V tomto případě vycházíme z objektového náhledu na reálný svět. Geoinformatika zde umožňuje vytvářet modely reálného světa, jejichž ústředním stavebním kamenem je modelový obraz objektu reálného světa – geoprvek (angl. feature). Ten si můžeme definovat například takto (Laurini, Thompson; 1994, Rapant, 2014):

Geoprvek je modelový obraz lokalizovatelného objektu reálného světa, který je dále nedělitelný na jednotky stejné třídy a který je popisovaný geodaty.

Uveďme si jednoduchý příklad (Rapant, 2014).

Příkladem geoprvku může být budova rektorátu Jihočeské univerzity, kterou již nelze rozdělit na budovy, ale může být rozdělena na patra, místnosti apod. Jiným příkladem může být silnice E55, řeka Malše, Stromovka, Kamenolom Zbraslav, Čertovo jezero, uhelná sloj Prokop apod. Všimněme si, že vždy se jedná o konkrétní geoprvek – modelový obraz konkrétního objektu reálného světa.

Na každý geoprvek se odkazujeme unikátním identifikátorem, například adresou, číslem parcely, unikátním kódem apod. Geoprvky mohou reprezentovat jak fyzické objekty reálného světa, tak i abstraktní objekty, jako jsou například volební obvody, statistické jednotky apod. Ačkoliv mohou být vnitřně složeny z více částí, mají jedinečnou reprezentaci.

Geoprvky seskupujeme na základě podobnosti vlastností do tříd geoprvků. Třídu geoprvků můžeme definovat takto (Rapant, 2006):

Třída geoprvků je tvořena skupinou geoprvků se společnými vlastnostmi. Je modelovým obrazem třídy objektů reálného světa.

Opět uvedeme jednoduchý příklad (Rapant, 2014).

Příkladem třídy geoprvků může být budova (obecně jakákoliv budova), les, strom, jezero, zlom apod. Vždy se jedná obecně o označení třídy geoprvků, nikoliv o konkrétní geoprvek. Kterákoliv z těchto tříd geoprvků je modelovým obrazem odpovídající třídy objektů reálného světa.

Složky popisu geoprvku

Každý geoprvek, má-li být správně reprezentován a zpracováván, musí být popsán z mnoha hledisek. Z pohledu geoinformatiky je důležitý popis polohy daného geoprvku v prostoru a jeho geometrických vlastností. Dále musí být popsány negeometrické vlastnosti geoprvku – tzv. atributy (název, počet pater, pórovitost, hustota, hloubka uložení…). V neposlední řadě musí popis geoprvku zaznamenat jeho trvání a proměny v čase a jeho vztahy k okolním a případně i jiným geoprvkům. Zapomenout nesmíme ani na popis operací, které lze s daným geoprvkem provádět (nebo činností, které může daný geoprvek vykonávat) a na specifikaci kvality popisu, která by měla doprovázet každý popis geoprvku (Rapant 2006).

Popis geoprvku prostorovými daty je proto možné rozdělit na pět základních složek (Rapant, 2006):

• geometrickou – zaznamenává polohu geoprvku v prostoru a popisuje jeho geometrické vlastnosti,
• popisnou (někdy též označovanou jako tematickou) – zaznamenává negeometrické vlastnosti geoprvku,
• časovou – zaznamenává historii změn geoprvku v čase; lze z ní odvodit dobu existence geoprvku v daném stavu,
• vztahovou – popisuje vztahy, do nichž geoprvek vstupuje s jinými geoprvky, mimo jiné i prostorové vztahy s okolními geoprvky – tzv. topologii,

• funkční – popisuje operace, které lze s daným geoprvkem provádět, a jako doplňující složka, která se nevztahuje přímo k popisovanému geoprvku, nýbrž k jednotlivým složkám jeho popisu jako takovým, je složka:

• kvalitativní – popisuje kvalitu popisu geoprvku.

Následující text je věnován podrobnějšímu rozboru jednotlivých složek.

Geometrická složka popisu geoprvků je z hlediska geoinformačních systémů velice důležitá a nesmí být nikdy opomenuta, měla by být vždy definovaná na požadované úrovni rozlišení a přesnosti. Je s ní svázáno několik okruhů problémů:

• prostor, v němž je geometrická složka definována,
• určení polohy geoprvku v tomto prostoru,
• prostorové vlastnosti geoprvku.

U každého geoprvku je nezbytné zaznamenat prostor, v němž je definována jeho geometrická složka popisu, neboť na tomto prostoru závisí, jak bude možné s geoprvkem pracovat.Geoprvky jsou zpravidla primárně definovány v Euklidovském prostoru, ale může nastat i situace, kdy jsou definovány primárně v topologickém nebo i jiném prostoru.

Určení polohy geoprvku je závislé na prostoru, v němž je definován. V případě Euklidovského prostoru je poloha geoprvku vyjádřena přímo souřadnicemi nebo nepřímo geokódem, v případě topologického prostoru prostorovými vztahy k okolním geoprvkům apod.

Mezi prostorové charakteristiky geoprvku patří např. (Lurini, Thompson, 1994):

• délka (například úseku silnice nebo řeky, vedení vysokého napětí),
• rozloha (například jezera, okresu, parcely),
• objem (například zásob uhlí, nebo náspu nezbytného pro vybudování silnice),
• tvar (kruhový, čtvercový, protáhlý),
• nepravidelnost tvaru (například klikatá pobřežní linie),
• orientace (například hlavních os oblíku),
• střed liniového geoprvku nebo plochy (například střed města, středová linie silnice),
• sklon (například svahu).

Měření těchto vlastností je zpravidla jednoduché. Přesnost jejich stanovení je závislá jednak na použitých přístrojích, jednak na postupech a jednak na měřítku podkladových materiálů. Například délka pobřežní linie jezera bude různá při měření v reálných podmínkách krokováním, pásmem, měřickými postupy a bude odlišná i při odměření na mapách v měřítku 1 : 100 000 nebo v měřítku 1 : 1 000.

Tematická složka popisu geoprvku je tvořena tak zvanými atributy (v užším slova smyslu; angl. attribute), které popisují negeometrické vlastnosti geoprvků. Každý atribut je obecně tvořen párem: název vlastnosti – hodnota vlastnosti (Frank 1987). Název udává, jaká vlastnost geoprvku je hodnotou popisována. Každý geoprvek smí mít pro každý atribut (tedy každou vlastnost) přiřazenu nejvýše jednu hodnotu.

Hodnoty každé vlastnosti jsou vybírány z určitého definičního oboru, který je nazýván doména (angl. domain). Doménu je možné charakterizovat jako potenční množinu dat, ze kterých je vybírána hodnota atributu (Horák, 2011). Může jí být např. obor celých čísel, interval na reálné ose, nebo výčet možných hodnot apod. Pro různé vlastnosti jsou vhodné různé domény.

V zásadě lze rozlišit následující typy domén:

• nominální (výčtové) – např. pro typ silnice to může být (dálnice, silnice pro motorová vozidla, 1. tř., 2. tř., 3. tř., polní, neuveden, neznámý).
• ordinální (pořadové) – možné hodnoty jsou uspořádány, můžeme je tedy porovnávat (např.prvohory, druhohory, třetihory, čtvrtohory),
• intervalové – např. celá čísla z intervalu (0, 10), desetinná čísla z intervalu (0.5, 14.0);hodnoty lze sčítat, odčítat, jejich rozdíl je interpretovatelný; stupnice však nemá absolutní nulu, proto je nelze poměřovat; příkladem je teplota uvedená ve \(^{o}\)C),
• poměrové – jakákoliv stupnice mající absolutní nulu, např. procenta, teplota vyjádřená ve \(^{o}\)K apod.; tyto hodnoty lze i poměřovat.

Každý geoprvek smí mít pro každou vlastnost přiřazenu nejvýše jednu hodnotu.

Časová složka popisu geoprvku

Geografové i historici již odpradávna zdůrazňovali, že pro správné porozumění objektům, jevům, událostem a procesům v reálném světě je nezbytné brát v úvahu nejen jejich aspekty prostorové, ale i časové (tj. jak polohu v prostoru, tak i „polohu“ v čase) (Gregory 2002). Většina dnes komerčně dostupných programů pro tvorbu geoinformačních systémů však neumí s časem plnohodnotným způsobem pracovat. Je to dáno především tím, že zahrnutí času do datového modelu přináší celou řadu koncepčních problémů, které zatím představují určitou obtížně překročitelnou překážku. Pokud uživatel s časem pracovat potřebuje, je na něm, aby tento problém vyřešil sám na úrovni datového modelu své aplikace.

Bohužel komplexnost současného a soustavného zpracovávání prostorových a časových aspektů objektů, jevů, událostí a procesů reálného světa je tak veliká, že většinou musíme přistupovat ke kompromisu: buďto upřednostníme prostorové aspekty, zaznamenáváme je velice detailně v celé zájmové oblasti, ale musíme pak výrazně zjednodušit záznam v čase (tj. nemůžeme detailně zaznamenat vývoj v čase) nebo upřednostníme časové aspekty (tj. detailní záznam vývoje v čase) a musíme pak buďto výrazně snížit prostorový rozsah studované oblasti nebo výrazně snížit podrobnost zaznamenávaných prostorových aspektů.

Pequet (in Gregory, 2002a) uvádí, že geoinformační systém plně zpracovávající čas by měl být schopen odpovídat na tři typy dotazů:

1. Na změny objektů reálného světa, např. Změnil objekt reálného světa svoji polohu v posledních dvou letech?, Kde se objekt nacházel před rokem? nebo Jak se objekt změnil za posledních pět let?.
2. Na změny v prostorovém rozmístění objektů, např.: Které pozemky, které byly k 1.1.1990 zemědělsky využívané, se změnily do 31. 12. 2000 na pozemky určené pro občanskou výstavbu? nebo Jak byly rozloženy pozemky určené ke komerčním aktivitám k 31.12.1995?.
3. Na časovou souvislost více geografických fenoménů, např.: V kterých oblastech došlo k sesuvům půd do jednoho týdne po výskytu přívalových dešťů?.

Čas se svojí povahou výrazně liší od geometrických a popisných vlastností geoprvku. Snad především tím, že nemůže být chápán jako složka popisu sama o sobě, ale vždy v těsném vztahu k výše uvedeným složkám popisu geoprvku (Obr. 54). Proměny v čase jsou zaznamenávány sérií verzí geometrické a tematické složky popisu geoprvků.

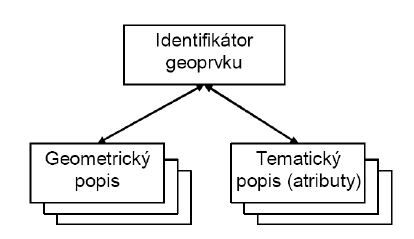
Obrázek 2: Vztah času ke geometrické a tematické složce popisu geoprvku. Změny v čase jsou zde zachyceny jednotlivými verzemi geometrického a tematického popisu (zdroj: Rapant, 2014)

Vztahová složka popisu geoprvku

Jednotlivé objekty reálného světa mohou vstupovat do vzájemných vztahů s jinými objekty reálného světa. Přitom některé z těchto vztahů mohou být odvozeny z dat (jsou tedy vyjádřeny implicitně), jiné vztahy je nezbytné zadat explicitně, jako například vlastnické vztahy. Vztahová složka popisu geoprvku je zaměřena právě na popis těchto vztahů.

Vztahy mezi objekty reálného světa mohou být:

1. topologické,
2. časové,
3. metrické,
4. syntaktické,
5. je částí (angl. part-of),
6. ostatní (např. vlastnické).

Topologické vztahy

Tabulka 1 obsahuje příklady prostorových vztahů tak, jak se s nimi setkáváme v reálném světě.

Tabulka 1: příklady prostorových vztahů

vztah	typický příklad
náleží/přísluší/patří	obec patří do okresu, úsek el. vedení přísluší do souvislé sítě vyššího řádu
obsahuje/je složen z	stát je složen z krajů, ty obsahují obce
umístěn (nachází se) v/na	daná budova se nachází na konkrétní parcele
hranice	dvě parcely mají společnou hranici

Zatímco v běžných analogových mapách je většina těchto vztahů obsažena implicitně, uživatel je vnímá intuitivně, tak v digitálních mapách musí být vyjádřeny explicitně, protože počítač nemá žádnou intuici. Počítačové zpracování vzájemných vztahů geoprvků proto vyžaduje doplňující informace popisující tyto vztahy nebo vyžaduje instrukce, popisující, jak mohou být tyto informace získány přímo z dat.

Některé vztahy, do nichž mohou geoprvky vstupovat, navíc závisí na konkrétním stavu, v němž se nachází zobrazovaná realita. Například v rozvodných sítích může stav ventilů určovat, které části sítí mohou být považovány za jednu logickou jednotku. Za takovéto situace je nezbytné rozlišovat ještě aktuální a potenciální vztahy.

Příklad (Rapant, 2014): Mějme plynovodní potrubí a zkoumejme propojení dvou oblastí, tj. zda jsou topologicky propojené. Mezi těmito oblastmi vede plynovodní potrubí, jehož součástí je šoupě, umožňující přerušit průtok plynu potrubím. Je-li šoupě uzavřené, je aktuální topologický vztah mezi oblastmi „nepropojené“ a potenciální topologický vztah je „propojené“.

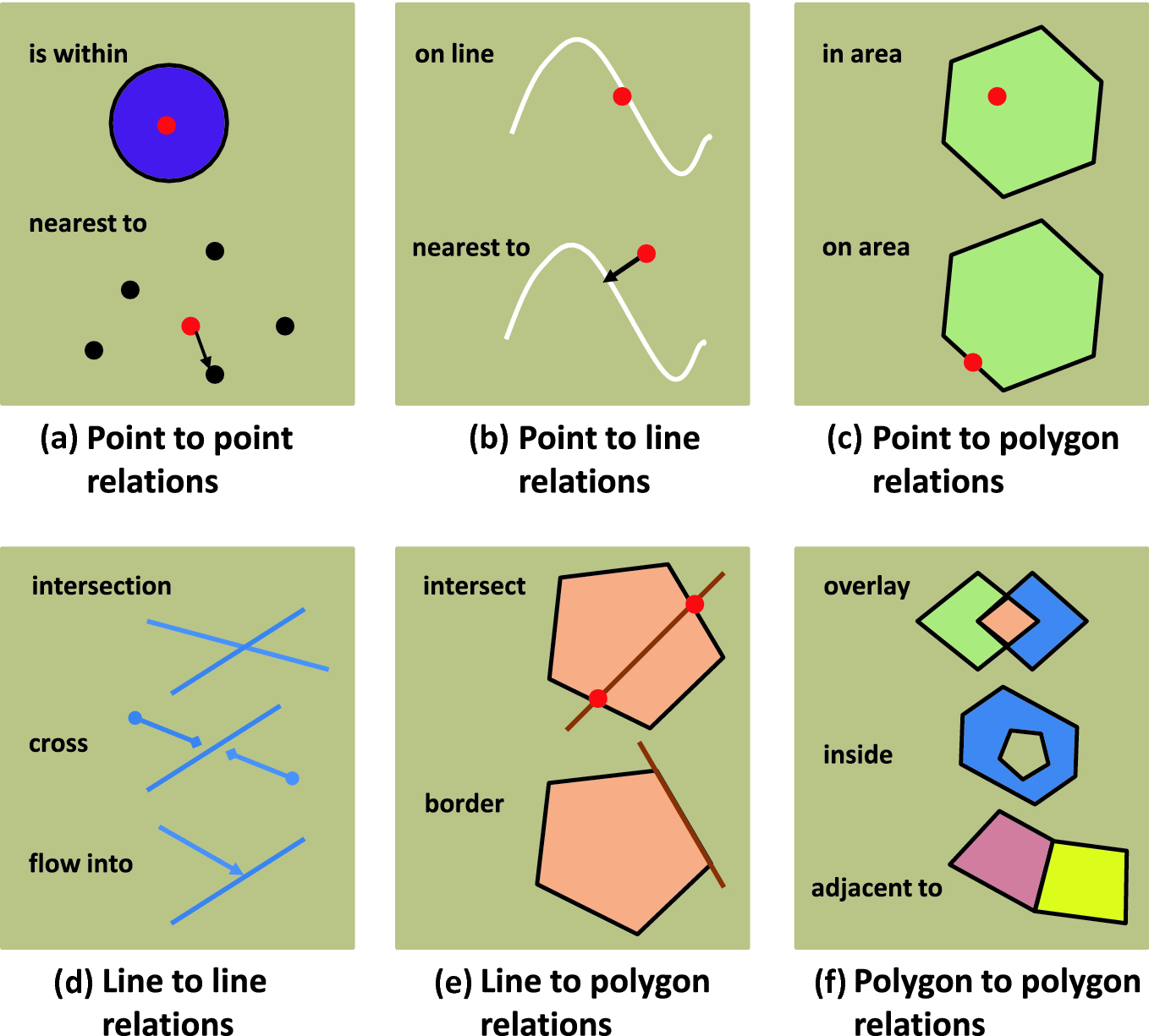
Příklady topologických vztahů mezi geoprvky různých dimenzí ukazuje obrázek 3.

Časové vztahy geoprvků mohou být následující (Rapant, 2014):

• nahodilý spoluvýskyt – geoprvek se vyskytuje zcela nahodile, nemá žádný explicitně vyjádřený kauzální vztah k jiným geoprvkům (například pole a potok),
• vztah koexistenční – geoprvek se vyskytuje současně s jinými geoprvky (např. existence parkoviště je vázána na existenci příjezdové komunikace),
• vztah sukcesivní (následný) – geoprvek se vyskytuje s časovým odstupem po vzniku jiného geoprvku (např. tzv. brownfieldy, které vznikají po ukončení výroby v průmyslové zóně),
• vztah kauzální (příčinný) – geoprvek vznikne jako přímý důsledek vzniku jiného geoprvku (vodní plocha vznikne jako důsledek vzniku terénní překážky – umělé hráze, přehrazení údolí sesuvem půdy apod.).

K metrickým vztahům patří především přímá vzájemná vzdálenost geoprvků. Tyto vztahy se nevyjadřují explicitně, zpravidla se odvozují přímo z geometrické složky popisu geoprvků s využitím metriky zvoleného prostoru.

Syntaktické vztahy

Syntaxe obecně vyjadřuje, které geoprvky mohou (nebo v některých případech dokonce i musí) mít vzájemný topologický a případně i metrický a časový vztah a které naopak určitý vztah mít nesmí.

Příklady (Rapant, 2014): Křižovatka dvou silnic: může existovat křižovatka dvou dálnic resp. dálnice a silnice první třídy, ale nesmí existovat křižovatka dálnice a silnice druhé nebo třetí třídy apod. Pumpa se musí vždy nacházet u silnice, nemůže stát někde mimo, bez napojení na silniční síť. Řeka se může vlévat do jiné řeky, jezera nebo moře, ale určitě ne např. do dálnice.

Vztah „je částí“ vyjadřuje skladebnost geoprvků. Například republika je složena z krajů, tj. kraj „je částí“ republiky. Předpokládá se přitom, že složením všech krajů dohromady vznikne celá republika (kompletní pokrytí) a že kraje jsou vzájemně disjunktní (nepřekrývají se).

Tento typ vztahů se částečně překrývá se vztahy topologickými a případně i syntaktickými, ale nemusí tomu tak být vždy.

Příklad: Na krajích si můžeme jednoduše demonstrovat použití různých druhů vztahů:

• topologické vztahy říkají, který kraj sousedí s kterým,
• syntaktické vztahy říkají, že kraj obecně může sousedit s jiným krajem nebo s jiným státem,
• vztah „je částí“ říká, že kraj je částí státu, jednotlivé kraje jsou disjunktní a všechny kraje dohromady pokrývají území celého státu.

Do kategorie ostatních vztahů můžeme zařadit všechny vztahy, které se netýkají ani prostoru ani času. Mohou sem patřit například vlastnické vztahy, vztahy nadřízenosti a podřízenosti, vztahy členství apod. Tyto vztahy se vyjadřují explicitně.

Obecně je složce popisu vztahů geoprvků věnována explicitně jen malá pozornost (samozřejmě s výjimkou topologie), proto je její detailnější rozpracování otázkou spíše bližší budoucnosti. V geoinformačních systémech je tato složka realizována zpravidla v rámci datového modelu.

Funkční složka popisu geoprvku je zaměřena na popis operací, které je možné s geoprvkem provádět. Tyto operace obvykle vedou ke změně stavu jedné nebo více složek jeho popisu (a tím i ke změně stavu geoprvku jako takového).

Jako příklad těchto operací lze uvést:

• změna vlastnictví u nemovitosti,
• postavení nového domu,
• zboření domu,
• přestavba domu,
• změna příslušnosti obce k okresu,
• změna názvu obce,
• spojení dvou obcí,
• změna vedení rozvodné sítě,
• zablokování provádění jakýchkoliv změn,
• odblokování provádění jakýchkoliv změn, apod.

Tyto operace popisují události v reálném světě. Popisují tedy, jaké činnosti musí předcházet dosažení nového stavu. Jejich přesný popis se v podstatě rovná popisu chování reálného systému.

Příklad (Rapant, 2014): Mějme parcelu. Řekněme, že povolené operace s parcelou jsou:

• sloučení dvou parcel,
• rozdělení parcely,
• změna vlastníka parcely.

Pokud bude chtít někdo provést jinou manipulaci s parcelou, například přesunout ji na jiné místo, nebude tato operace akceptována.

Pro tuto složku platí obecně stejný závěr, jako v případě složky předešlé. Dnes jí zatím není samostatně věnována dostatečná pozornost. Jedinou výjimkou jsou snad jen objektově orientované systémy.

V geoinformačních systémech se tato složka popisu geoprvku realizuje prostřednictvím programového kódu, který provádí manipulace s geoprvkem tak, aby bylo dosaženo požadovaného stavu.

Kvalitativní složka popisu geoprvku, metadata

Data obsažená v prostorových databázích jsou obecně multidimenzionální povahy. A stejnou (multidimenzionální) povahu mají i chyby těchto dat. Z toho vyplývá, že chybu určení konkrétního prostorového údaje nelze popsat jednoduchým indexem.

Např. prostorová přesnost zahrnuje jak horizontální, tak i vertikální složku, které nelze vždy oddělit. Tematická přesnost závisí na typu dat (např. numerická nebo kategorická) a mnohdy i na prostorové přesnosti. Časová přesnost je důležitá, avšak často přehlížená dimenze přesnosti prostorových databází. A o přesnosti popisu vztahů a operací se dodnes nemluví vůbec.

Spolehlivost dat je často (i když ne vždy) inverzní funkcí jejich stáří, protože všechny složky popisu geoprvku se mohou v čase měnit. A navíc popisy geoprvků získané v dřívějších dobách pomocí dřívějších metod mají často (alespoň z dnešního pohledu) omezenou, nebo dokonce neznámou přesnost.

Kvalita popisu geoprvku je obvykle dokumentována následujícími parametry, označovanými jako metadata (Horák 2002):

• přesnost geometrické složky popisu geoprvku, definovaná obvykle
  • přesností horizontální složky,
  • přesností vertikální složky,
• úrovní rozlišení (např. zda bude vodní tok reprezentován jednou linií, kopírující střed toku, nebo bude reprezentován dvěma liniemi, kopírujícími oba břehy),
• rozsahem geografického pokrytí,
• způsobem reprezentace (diskrétní vs. kontinuální),
• přesnost tematické složky popisu geoprvků, definovanou obvykle přesností jednotlivých atributů,
• přesnost časové složky popisu geoprvků, definovanou obvykle
  • aktuálností jednotlivých složek,
  • intervalem aktualizace,
• logická bezespornost mezi geometrickou a popisnou složkou,
• kompletnost, daná
  • kompletností dat,
  • kompletností modelu,
  • kompletností atributů,
  • kompletností hodnot,
• relevance popisu geoprvku (pro které operace je možné popis geoprvku použít, případně pro které ne).

Tyto parametry mohou být sledovány buďto na úrovni jednotlivých geoprvků, pokud je to opodstatněné, nebo spíše na úrovni skupin stejných geoprvků (například pro všechny silnice zaměřené ve stejném období stejnou metodou bude definována jedna sada těchto parametrů), zahrnutých obvykle do tzv. datových sad (angl. data set). Přípustná je i kombinace obou přístupů. Datovou sadu můžeme definovat takto:

Datová sada je identifikovatelná kolekce dat.

Dnes se o této složce popisu geoprvků mluví poměrně intenzivně, hlavně ve spojitosti s budováním tzv. metadatových služeb (angl. metadata service), které mají uživatelům poskytovat informace o existenci jednotlivých datových sad a dále metadata je popisující. Uživatel se pak může na základně poskytnutých údajů snadno rozhodnout, zda je vyhledaná datová sada vhodná pro jeho potřeby. Vzhledem k tomu, že metadata zpravidla obsahují i údaje o poskytovateli datové sady, může ho uživatel v případě kladného závěru i přímo oslovit.

2.2.2 Modelování jevů v geoinformatice

Pro modelování jevů reálného světa používá geoinformatika celou řadu různých tzv. sítí (angl. net), jejichž základním stavebním kamenem je zpravidla buňka (angl. cell), reprezentující vymezenou část prostoru reálného světa a nesoucí hodnoty sledovaných vlastností. Nejběžněji používanou je pravidelná síť čtvercových buněk, které se říká rastr (angl. raster).

Rastry známe z digitálních fotografií. Zde je každé buňce rastru (v tomto případě mluvíme spíše o pixelech) přiřazena barva sejmutá ze snímaného z prostoru a vnímáním celého rastru si v mozku vytvoříme vjem obrázku snímané reality.

U rastru postupujeme obdobně. Každá buňce rastru přiřadíme hodnotu sledované vlastnosti (např. teploty vzduchu v místnosti). Kdybychom si prohlíželi jen číselné hodnoty, obtížně bychom si vytvářeli představu o rozložení teploty v prostoru. Při vizualizaci rastru proto používáme obdobný princip, jako u digitální fotografie. Nalezneme minimální a maximální hodnotu sledované vlastnosti v rastru a vytvoříme si převodní barevnou stupnici, která umožní každé číselné hodnotě přiřadit konkrétní barevný odstín. Tím převedeme matici čísel na barevný obrázek, jehož vjem nám umožní získat ihned velice dobrou představu o rozložení hodnot teploty vzduchu v prostoru.

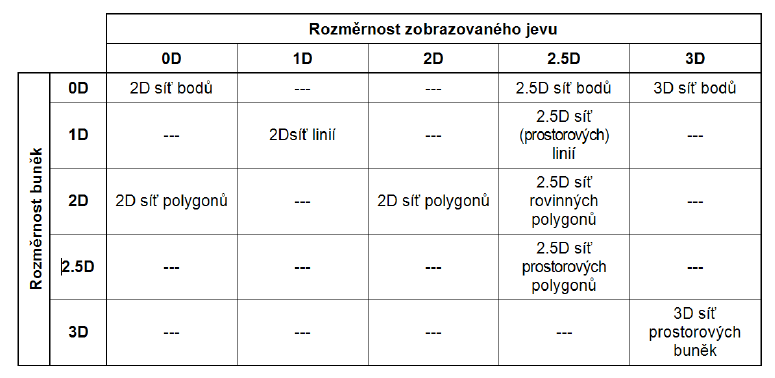
Možné kombinace rozměrnosti zobrazovanch jevů reálného světa, buněk použitých k jejich reprezentaci a rozměrnosti výsledné sítě buněk (Rapant, 2006) ukazuje tabulka 2.

Složky popisu sítě buněk

Každá síť buněk, má-li správně reprezentovat daný jev reálného světa a má-li být správně zpracována, musí být popsána z několika hledisek:

• Jednak musíme mít k dispozici informace o vlastnostech zobrazovaného jevu,
• dále informace o vlastní síti buněk a
• o vlastnostech buněk sítě.
  

Složka popisu vlastností zobrazovaného jevu

Každý zobrazovaný jev reálného světa je nezbytné popsat prakticky ze stejných hledisek, jako je tomu v případě geoprvků. To znamená, že i zde pracujeme s následujícími složkami popisu jevů:

• geometrická,
• tematická,
• časová,
• funkční,
• vztahová,
• kvalitativní.
  

S geometrickou složkou popisu jevu reálného světa jsou spojeny následující problémy:

• prostor, v němž se jev vyskytuje (v němž je popisován) a jeho dimenzionalita,
• prostorová spojitost jevu,
• prostorové vymezení jevu.

Prostor - v tomto případě nás zajímá, v jakém prostoru se daný jev vyskytuje, kolik má tento prostor rozměrů a jak je v něm jev rozložen.

Prostorová spojitost popisuje, jak se mění hodnoty vlastností daného jevu při změně polohy v prostoru. Obecně rozeznáváme jevy spojité, kdy s plynulou změnou polohy se plynule mění i hodnoty sledovaných vlastností a jevy diskrétní, kdy se hodnoty vlastností mění skokem a případně pro některé oblasti prostoru nejsou ani definované.

Prostorové vymezení v podstatě udává hranice studovaného jevu v prostoru.

Tematická složka popisu jevu zahrnuje informace o negeometrických vlastnostech zobrazovaného jevu, tj. výčet a popis těchto vlastností, popis jejich typů apod.

Časová složka popisuje chování zobrazovaného jevu v čase a případně charakterizuje dynamiku jeho vývoje (rychlost a četnost změn apod.). Rozlišujeme jevy:

• statické,
• dynamické.
  

Vztahová složka popisuje možné závislosti zobrazovaného jevu na jiných jevech, objektech a procesech reálného světa.

Funkční složka - předmětem této složky popisu jsou operace aplikovatelné na daný jev.

Kvalitativní složka charakterizuje, jak kvalitní informace se nám podařilo získat v rámci sestavování předcházejících složek popisu zobrazovaného jevu.

Složka popisu vlastností sítě

Složka popisu vlastností sítě popisuje síť použitou pro reprezentaci zobrazovaného jevu z následujících hledisek:

• rozměrnost sítě,
• typ sítě,
• velikost sítě,
• způsob přiřazování hodnot vlastností buňkám,
• interpolace hodnost v rámci sítě.
  

Rozměrnost sítě popisuje počet dimenzí sítě - zpravidla 2D, 2.5D nebo 3D síť.

Typ sítě popisuje, zda je síť pravidelná (složená z buněk stejných rozměrů a tvarů) nebo nepravidelná (buňky různých rozměrů a tvarů).

Velikost sítě má význam především v případě pravidelných sítí, kdy by měl být popsán počet buněk ve směru jednotlivých dimenzí a případně i celkový počet buněk. V případě nepravidelné sítě bude tento popis komplikovanější a bude záviset jednak na vlastnostech sítě a jednak na dohodě nebo přijatém standardu. Může být zadána i explicitně hranicí sítě.

Způsob přirazování hodnot vlastností buňkám popisuje způsobe, jakým bude určena hodnota každé vlastnosti zobrazovaného jevu, která bude přiřazena buňce.

Interpolace hodnot v rámci sítě - popis interpolačního mechanismu, který bude použit při interpolaci hodnost v rámci sítě, tj. např. výpočet hodnot dané vlastnosti zobrazovaného jevu pro buňky, jimž nebyla přiřazena hodnota této vlastnosti.

Složka popisu vlastností buňky

Tato složka může existovat ve dvou podobách v závislosti na tom, je-li síť složena z buněk se stejnými vlastnostmi či ne. V prvním případě se jediný popis vztahuje na všechny buňky sítě, ve druhém má každá buňka přiřazený svůj vlastní popis. V každém případě by však vlastností buňky sítě měl postihnout následující aspekty:

• rozměrnost buňky,
• tvar buňky,
• velikost buňky,
• interpolace hodnost v rámci buňky,
• souřadnice buňky.

Rozměrnost buňky popisuje počet rozměrů buňky - v úvahu v tomto případě přicházejí všechny možnosti ze škály 0D až 3D.

Tvar buňky popisuje tvar, která má buňka. Ten může být buď pravidelný nebo nepravidlený, a dále může být blíže charakterizován konkrétním vzorem, jako je bod, úsečka, kruh, šestiúhelník, krychle apod.

Velikost buňky popisuje např. délku strany pravidelného tvaru nebo délky jednotlivých úseček tvořích hranici buňky a úhly jimi sevřené (v případě nepravidelné buňky omezené přímými úseky hranice) apod.

Interpolace hodnot v rámci buňky - v některých případech (např. digitálních modelů reliéfu) se hodnoty vlastností jevu nepovažují za konstantní v rámci buňky, ale odvozují se interpolací z hodnot vztahujících se např. k vrcholům buňky. V takovém případě je nezbytné stanovit interpolační mechanismus umožňující odvozovat hodnoty těchto vlastností kdekoliv na ploše buňky.

Souřadnice buňky - zde je popsán buďto způsob odvozování souřadnic kterékoliv buňky (v případě pravidelné sítě) nebo jsou zde uvedeny přímo souřadnice té buňky, k níž se popis vztahuje (v případě nepravidelné sítě).

2.3 Prostor v geoinformatice

Definovat pojem prostor je velice obtížné. Samo pojetí prostoru je velice široké, sahá na jedné straně od reálného fyzikálního prostoru (tedy prostoru, který známe ze svých každodenních zkušeností) až po abstraktní prostor na straně druhé. Ten je běžně definován jako množina prvků, která má některé výrazné rysy reálného fyzikálního prostoru. Pro člověka je běžné, že pracuje s různými pojetími prostoru a běžně a bez obtíží mezi nimi přechází. Může si tak volit takové pojetí prostoru, které nejlépe odpovídá řešenému úkolu. Například pokud potřebujeme stanovit plochu parcely, budeme pracovat v tzv. Euklidovském prostoru. Pokud budeme řešit úlohy typu nalezení vhodné trasy pro jízdu mezi dvěma městy po silnici, budeme pracovat s prostorem, kde nás zajímá, která města jsou propojená silnicemi, ale nemusí nám přitom záležet na znalosti přesné polohy měst a silnic. V tomto případě budeme pracovat v tzv. topologickém prostoru a budeme využívat nástrojů teorie grafů.

I když tato různá pojetí prostoru se v běžném životě používají bez nároku na jejich formální popis, při přechodu do prostředí počítačově orientovaných informačních systémů je formalizace nezbytná (Kolář 1997).

2.3.1 Historický vývoj pojetí prostoru

Z hlediska geoinformatiky je velice významnou myšlenka duality pojetí prostoru jako kontinuálního pole resp. množiny diskrétních objektů. V praxi to znamená, že se na prostor díváme buďto jako na spojitý prostor, v němž je definována (nekonečná) množina míst (nebo též množina bodů), ke kterým se vztahují hodnoty sledovaných (negeometrických) vlastností tohoto prostoru nebo jako na diskrétní prostor, tvořený (konečnou) množinou objektů reálného světa, které mají explicitně vyjádřenu svoji polohu v prostoru, geometrické vlastnosti, topologické vztahy a teprve k těmto objektům reálného světa jsou vztaženy negeometrické vlastnosti (obrázek 4).

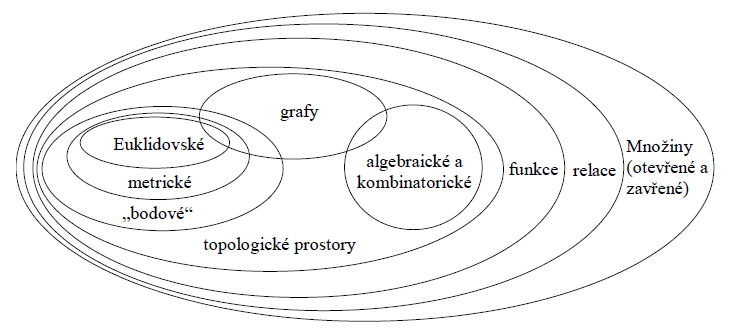
Obrázek 4: Hierarchické členění matematických prostorů (zdroj: Rapant, 2014)

Dualita našeho pojetí prostoru má fundamentální dopad na geoinformatiku a na prostorové modelování a analýzu obecně. To se odráží mimo jiné v reprezentaci prostoru v geoinformačních systémech, kde se běžně používají dva základní přístupy (Gahegan, 1995 in Rapant,2014):

• prostor je definován jako množina míst, jimž jsou přiřazeny negeometrické vlastnosti (tj. pojetí „kontinuální“ – pole), nebo
• je prostor definován jako množina objektů (tj. pojetí diskrétní – objekty) majících prostorové vlastnosti (jako je tvar, poloha, topologie apod.) i negeometrické vlastnosti.

Tyto dva rozdílné přístupy mají přímý dopad na reprezentaci reálného světa v geoinformačních systémech.

2.3.2 Matematické prostory

Na obrázku 4 je schematicky znázorněno hierarchické členění matematických prostorů, tak jak je uvedeno v práci (Albrecht, Kemppainen 1996 - in Rapant, 2014). Na nejnižší úrovni je zde položeno pojetí prostorů jako množin objektů, které jsou bez jakékoliv vnitřní struktury. Uvnitř těchto množin je možné definovat pouze jednoduché vztahy typu členství.

O stupínek výše stojí podmnožina prostorů, umožňujících definovat relace mezi dvěma i více množinami. Tento vcelku jednoduchý konceptuální model prostoru je využíván při práci s relačními databázemi. Podmnožinou konceptuálního prostoru relací je prostor funkcí, který umožňuje transformovat každého člena první množiny na člena druhé množiny.

Topologické prostory, stojící opět o stupínek výše, se poprvé přibližují k pojetí prostoru, tak jak je vnímán lidmi. Při pohledu na obrázku 4 snadno zjistíme, že se topologické prostory dělí na dvě základní skupiny: bodové a algebraické. Zatímco topologie bodů pracuje s pojmem okolí, algebraická topologie představuje základ grafů.

Pokud zavedeme do tohoto prostoru i vzdálenost, dostáváme se do podmnožiny tzv. metrických prostorů. Metrické prostory musí splňovat některé podmínky, týkající se právě měření vzdáleností. Euklidovský prostor, stojící na špici naší hierarchie, zavádí poslední důležitou vlastnost, a tou je směr.

Koncepce prostoru v geoinformačních systémech není jednoduchá a plně využívá oné výše naznačené šíře. Tyto systémy běžně pracují s celou řadou prostorů. Nejzákladnějším z nich je prostor, v kterém jsou definované geometrické vlastnosti geoprvků. Ten má nejblíže k reálnému fyzikálnímu prostoru. Prakticky vždy se jedná o Euklidovský prostor. Geometrické vlastnosti geoprvků jsou v něm popisované pomocí vhodného souřadnicového systému.

Jedním z hlavních účelů geoinformačních systémů je provádění prostorových analýz. Tyto analýzy nemusí být nutně prováděné ve stejném prostoru, který je použit pro definování geometrických vlastností geoprvků. Příkladem mohou být analýzy typu Najdi v síti silnic nejkratší cestu z místa A do místa B.. Pro takovéto analýzy nepotřebujeme dokonce znát jakékoliv souřadnice, stačí nám znát jen tzv. topologii silniční sítě. Tím se s našimi prostorovými analýzami dostáváme do topologického prostoru, kde neexistuje žádný souřadnicový systém a neměří se zde vzdálenosti.

A bylo by možné pokračovat dalšími příklady prostorových analýz a jim odpovídajících prostorů.

Výše uvedené skutečnosti lze shrnout následovně:

Geoinformační systémy pracují s různými prostory. Jeden z nich lze považovat za základní, a tím je prostor, v němž je definována geometrická složka popisu geoprvků. Většinou se jedná o Euklidovský prostor. Dále zde existuje celá řada dalších prostorů, v nichž jsou prováděny prostorové analýzy a v kterých jsou případně i poskytovány výsledky těchto analýz.

Topologický prostor

Topologie je matematická disciplína, která studuje vzájemné prostorové vztahy geometrických objektů. Pro topologii je typické, že nepracuje se souřadnicemi těchto objektů. Někdy se jí také říká geometrie bez souřadnic (angl. rubber sheet geometry) (Herring 1987 - In Rapant, 2014). Studuje prostorové vztahy objektů, které mohou být definované nezávisle na souřadnicovém systému. Pracuje tedy s tzv. topologickým prostorem. V oblasti geoinformatiky se pojmem topologie označují zpravidla přímo prostorové vztahy geoprvků.

Pro geoinformatiku má topologie jako matematická disciplína zvláštní význam: s její pomocí mohou být daleko snáze analyzovány a vizualizovány různé typy systémů, jako jsou katastrální mapy, komplexní ekologické podmínky, dopravní a inženýrské sítě apod. (Streit, 2000). V geoinformatice standardně pracujeme jen s topologií nejvýše dvourozměrných geoprvků, reprezentovaných body, liniemi a polygony. Řešení topologie třírozměrných geoprvků je stále ještě příliš obtížné na to, aby bylo zvládnutelné v rozumném čase i při použití dnešních relativně výkonných počítačů.

V každém moderním geoinformačním systému je znalost topologie zaznamenaných geoprvků nezbytným předpokladem pro úspěšné zvládání požadavků uživatelů. Např. má-li geoinformační systém poskytnout odpověď na otázku Které parcely leží v okolí silnice XY v obci Z? nebo Jaká je rozloha lesů ležících v okruhu do 100 km od uvažovaného místa výstavby nového závodu pro výrobu celulózy? atd., pak je znalost prostorových vztahů geoprvků nezbytná.

Příklady prostorových vztahů geoprvků jsou uvedeny v tabulce 3 a na obrázku 3. V zásadě se řeší vzájemné prostorové vztahy bodů, linií a polygonů. Prohlédněte si topologická pravidla v geodatabázi ArcGIS.

Tabulka 3: Příklady prostorových vztahů geoprvků (zdroj: Rapant, 2014)

prvek/prvky	topologický vztah k jiným prvkům
bod leží	na koncovém bodu (uzlu) linie - koincidence
bod leží	na hranici polygonu
bod leží	uvnitř polygonu
bod leží	vně polygonu
linie	nekříží sebe sama
linie	dotýká se polygonu
linie	protíná polygon
polygon je	jednoduchý/komplexní
dva polygony	se dotýkají
dva polygony	se protínají (překrývají)
dva polygony	jsou disjunktní

Metrické prostory

V metrických prostorech lze měřit vzdálenosti mezi libovolnými body v prostoru. V různých prostorech lze přitom zavádět různé předpisy pro měření vzdáleností (tzv. metriky).

Metrika musí obecně splňovat následující podmínky:

• \(d(A,B)\geq 0\) … podmínka nezápornosti vzdálenosti,
• \(d(A,B)=0\) právě tehdy, je-li \(A=B\) … podmínka totožnosti,
• \(d(A,B)=d(B,A)\) … podmínka symetrie,
• \(d(A,B)\leq d(A,C)+d(C,B)\) … podmínka trojúhelníkové nerovnosti.

Množina \(M\) s takovouto metrikou \(d\) je nazývána metrický prostor, který označujeme \((M, d)\). Prvky množiny \(M\) nazýváme body a její podmnožiny bodovými podmnožinami. Metrika je v podstatě zobecněním pojmu vzdálenost, a proto také číslo \(d(A, B)\) nazýváme vzdáleností bodů \(A\) a \(B\). Na téže množině bodů \(M\) můžeme definovat různé metriky; jestliže metriky \(d\) a \(e\) jsou různé, pak ovšem i metrické prostory \((M,d)\) a \((M,e)\) jsou různé.

V prostředí geoinformačních systémů se nejčastěji používají dvě metriky:

• Euklidovská, určená pro měření vzdáleností v prostorech s kontinuálními souřadnicovými systémy,
• Manhattanovská, určená pro měření vzdáleností v prostorech s diskrétními souřadnicovými systémy a v prostorech, kde je možné se pohybovat pouze podél dvou navzájem kolmých sítí rovnoběžek.

Euklidovská metrika (též Euklidovská vzdálenost - obrázek 5) je definovaná vztahem

\(d_{ij}=\sqrt{(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}}\).

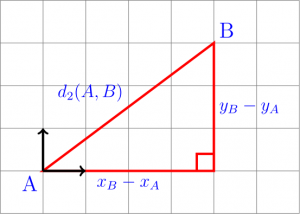
Obrázek 5: Euklidovská metrika (zdroj: https://dr-apeiron.net/doku.php/fr:vulgarisation:distance)

Jiný způsob měření vzdáleností byl navržen pro město Manhattan. Toto město je známé svojí téměř důsledně pravoúhlou sítí ulic. Z pohledu taxikáře je možné vzdálenosti v tomto Manhattanovském prostoru měřit pomocí Manhattanovské metriky definované vztahem (Maguire et al. 1991)

\(d_{ij}=|x_{i}-x_{j}|+|y_{i}-y_{j}|\).

Manhattanovská metrika je vhodná pro měření vzdáleností v oblastech s hustou pravidelnou zástavbou (např. i některé čtvrti našich měst).

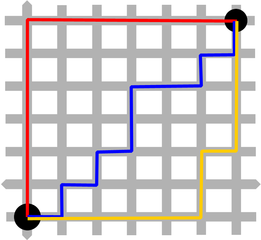
Obrázek 6: Manhattanovská metrika (zdroj: https://commons.wikimedia.org/wiki/File:Manhattan_distance_bgiu.png)

Ne ve všech prostorech, se kterými geoinformační systémy při prostorových analýzách pracují, jsou podmínky pro metrické prostory splněny. Při vyjadřování časové dostupnosti v úlohách na síti by například podmínka symetrie předpokládala, že doba jízdy do kopce je stejná jako doba jízdy z kopce. A obdobně lze dokázat i neplatnost trojúhelníkové nerovnosti. Důsledkem toho je, že z map časové dostupnosti obecně nelze odečítat jízdní časy mezi libovolnou dvojicí bodů, ale jen mezi počátkem a libovolným bodem, přičemž odečtená hodnota je platná jen pro jízdu směrem z počátku ke zvolenému bodu. Pokud by nás zajímala doba jízdy v opačném směru, museli bychom si vygenerovat novou mapu s počátkem v druhém z dvojice bodů. Takovýto „časový“ prostor proto nepatří do prostorů metrických.

Euklidovský prostor

Euklidovský prostor (angl. Euclidean space) je matematickou abstrakcí a rozšířením „běžného“, zpravidla třírozměrného prostoru, v němž se odehrává náš každodenní život. Jako první se jím zabýval Euclides cca 300 let před naším letopočtem. Sestavil systém postulátů a definic, z nichž byly odvozeny teorémy geometrie, které byly používány od nepaměti měřiči, konstruktéry, stavaři.

V 17. století zavedl Descartes (1596-1650) do Euklidovského prostoru pravoúhlý souřadnicový systém (říkáme mu kartézský souřadnicový systém – angl. Cartesian coordinate system) a umožnil tak propojení geometrie s aritmetikou a algebrou. Tím otevřel i cestu ke zobecnění Euklidovského prostoru i na více než třírozměrné případy.

\(N\)-rozměrný kartézský souřadnicový systém v n-rozměrném Euklidovském prostoru \(E_n\) se skládá z \(n\) navzájem kolmých souřadnicových os, které se protínají ve společném počátku a používají stejné měrné jednotky.

Každá uspořádaná \(n\)-tice reálných čísel \((x_1, x_2, \dots, x_n)\), kde \(x_i \in R\), definuje právě jeden bod \(v\) tomto souřadnicovém systému (a tím i v Euklidovském prostoru). V Euklidovském prostoru je definována metrika pro měření vzdáleností. Je to tedy prostor metrický.

Euklidovský prostor lze také definovat jako množinu bodů \(M\) reprezentujících \(n\)-tice vzniklé kartézským součinem (přesněji kartézskou mocninou definovanou nad množinou reálných čísel \(R\)). \(N\)-tice se pak označují jako souřadnice bodů množiny \(M\).

Náš reálný svět popisujeme jako třírozměrný Euklidovský prostor (\(E_3\)), nicméně pro potřeby zobrazování v geoinformačních systémech ho zpravidla převádíme na prostor dvourozměrný \(E_2\). Využíváme k tomu celou řadu postupů, které se nazývají kartografická zobrazení (viz dále).