Kapitola 4 Rastrová data

Základem rastrových dat je překrytí studované entity či oblasti pravidelnou sítí (mřížkou). Entita je pak popsána diskrétními hodnotami, které jsou vztaženy k polím této sítě. Polohová lokalizace entity je určena souřadnicemi polí, které ji představují (obrázek 1).

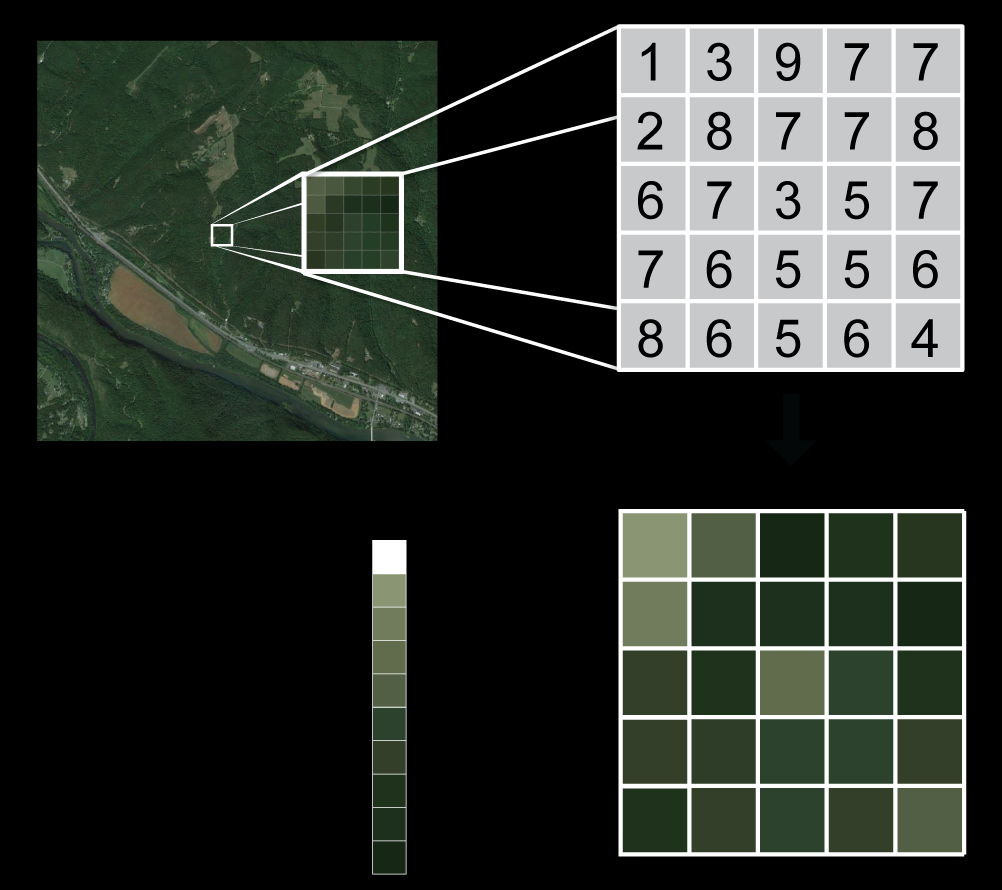
Obrázek 1: Koncept rastrových dat (zdroj: https://datacarpentry.org/organization-geospatial/01-intro-raster-data/)

Rastrová data jsou vhodná zejména pro reprezentaci spojitých fenoménů, jako je například:

• teplota vzduchu a vody,
• výška nad mořem,
• geologická data,
• mapa srážek,
• hustota povrchového odtoku,
• letecké a družicové snímkování a další.

Základní tvar buňky je odvozen ze základních geometrických tvarů, které splňují pravidla:

• nekonečné dělitelnosti buňky na buňky stejného tvaru a
• schopnost beze zbytku a bez překryvu vyplnit vymezenou plochu uspořádáním buněk vedle sebe.

Z uvedených požadavků na základní tvar buňky toto splňuje čtvercová, obdélníková a trojúhelníková buňka.V programových aplikacích GIS je rastr většinou tvořen maticí čtvercových buněk. Velikost (rozsah) rastru, jeho výška a šířka je dána počtem sloupců a řádků v matici a prostorovým rozlišením buňky. Řádky a sloupce bývají vůči sobě zpravidla kolmé a zpravidla bývají orientované rovnoběžně s osami kartézského souřadnicového systému.

Každý rastr je nutné připojit k souřadnicovému systému (georeferencovat). To se realizuje definicí souřadnic pro vztažný bod (střed nebo roh alespoň jedné buňky) rastru. Pokud rastr není připojen k souřadnicovému systému prostřednictvím vztažného bodu, má rastr jen tzv. obrazové souřadnice. Tzn. poloha každé buňky může být popsána jen číslem indexu popisujícím pozici buňky v rámci matice rastru, ve vztahu ke vztažnému bodu. Obrazové souřadnice jsou pro většinu GIS aplikací nepraktické. Proto se provádí v případě absence reálných souřadnic geometricka transformace obrazových souřadnic na reálné souřadnice.

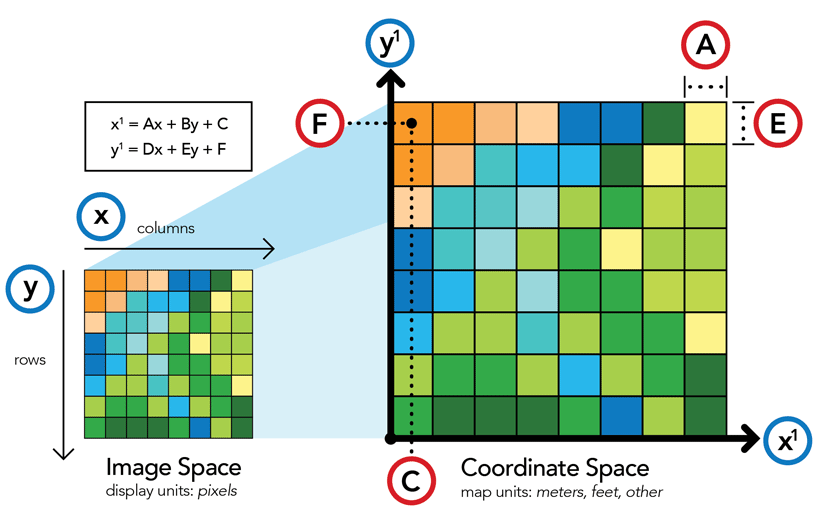
Obrázek 2: Georeferencování rastru (zdroj: https://www.esri.com/about/newsroom/arcuser/understanding-raster-georeferencing/)

V závislosti na formátu, který je zvolen pro uložení rastrových dat, může jeden rastrový soubor obsahovat více podobrazů se shodnými základní parametry matice rastru. Každý z podobrazů se pak liší hodnotami, které jeho buňky obsahují. Pro tyto dílčí rastry se používá název pásmo z anglického band (obrázek 3). Při zobrazování těchto rastrů se pak zobrazuje vždy kombinace třech pásem, kdy každé pásmo je zobrazeno pomocí jednoho barevného kanálu RGB. Tento přístup se velmi často používá u obrazových digitálních záznamů pořízených družicemi nebo u digitálních leteckých snímků.

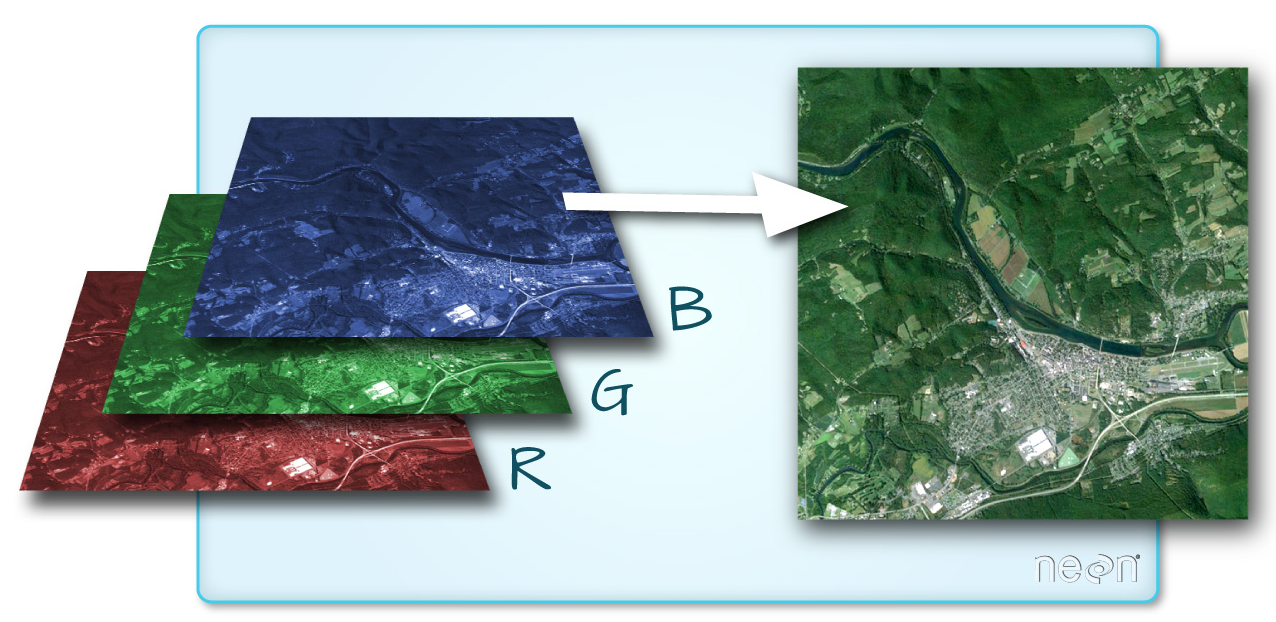
Obrázek 3: Vícepásmový rastr (zdroj: https://www.neonscience.org/dc-multiband-rasters-r)

Přehled rastrových formátů, užívaných v Geoinformatice naleznete GDAL00.

4.1 Typy dělení prostoru

Dělení prostoru lze provést dvěma základními způsoby (obrázek 4):

• pravidelná (regular) dělení prostoru - tvar buněk je přesně definován a vždy stejný - čtverec, obdélník, šestiúhelník, trojúhelník. Tyto rastry se dále dělí na
  • rastry se stejnou rozlišovací úrovní - jednotlivé buňky jsou stejně velk
    
  • rastry s nestejnou rozlišovací úrovní nebo hierarchické - velikost buněk se definovaným způsobem mění.
• nepravidelná (irregular) dělení prostoru, při kterých se vytvářejí buňky různého tvaru i velikosti.

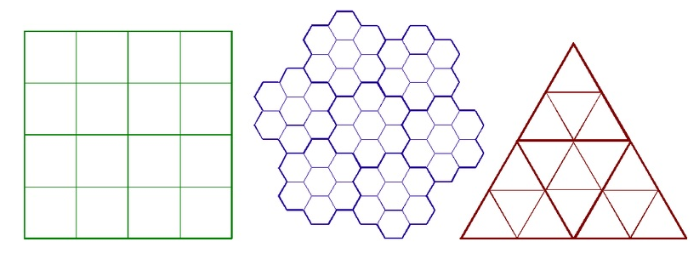
Obrázek 4: Různá dělení prostoru v rastrech

Praktické aplikace spočívají především v použití pravidelných tesselací (mozaiek), a to hlavně se stejnou rozlišovací úrovní. Hierarchické struktury jsou někdy chápány spíše jako metody komprese údajů. Historicky nejpoužívanější jsou rastry čtvercové, a to zejména z těchto důvodů:

• jsou kompatibilní s datovými strukturami používanými ve výpočetní technice (matice),
• jsou kompatibilní s mnoha hardwarovými zařízeními pro záznam a výstup údajů (skenery, tiskárny, plotry),
• jsou kompatibilní s kartézskými souřadnicovými systémy.

Pouze buňky tvaru čtverce lze rozdělit na menší čtverce se stejným tvarem a orientací. Základní prostorové buňky rastru nazýváme buňky rastru (cells) nebo pixely (pixel - picture element). Trojrozměrná varianta pixelu se nazývá voxel. Někdy dochází k záměně pojmů, např. je termín “rastr” používán ve významu “buňka rastru”, v pravém slova smyslu však rastr znamená systém pod pravým úhlem se protínajících čar, které ohraničují jednotlivé buňky. Pokud bereme v úvahu systém průsečíků těchto čar, jde o bodový rastr - lattice. V bodovém rastru se tématické údaje vztahují k přesné poloze v prostoru, v buňkovém k části plochy reprezentované buňkovým elementem.

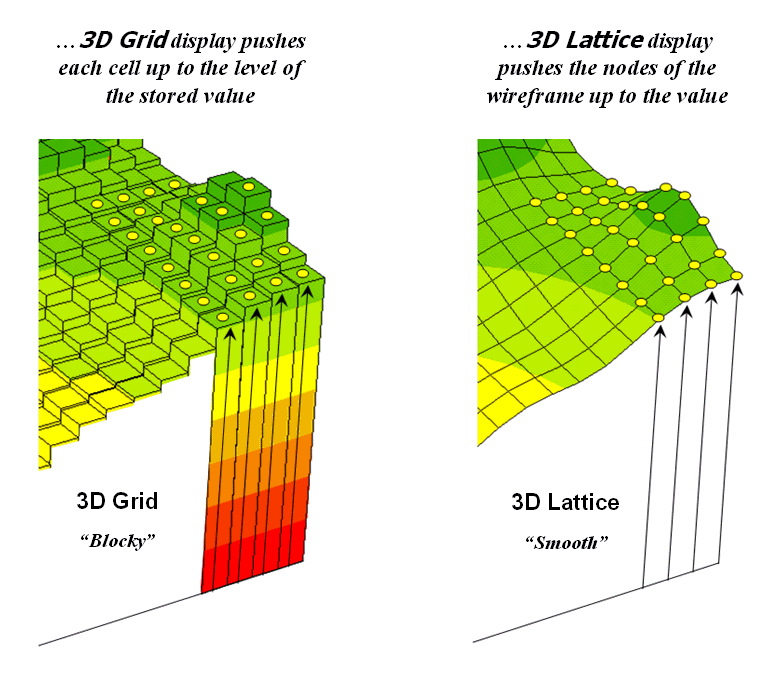
Obrázek 5: Plošný a bodový rastr v 3D (zdroj: https://blogs.ubc.ca/advancedgis/schedule/slides/spatial-analysis-2/lattices-vs-grids/)

Hlavní výhodou hexagonální mřížky je, že jsou středy všech sousedních buněk od středu dané buňky stejně vzdálené. Tato symetrie činí model výhodným pro některé analytické funkce, např. pro radiální prohledávání, což není možné u čtvercové nebo trojúhelníkové sítě. Hexagonální buňky se však v praxi používají jen zřídka. Základní charakteristikou všech trojúhelníkových tesselací je, že trojúhelníky nemají stejnou orientaci, což je výhodné pro reprezentace terénu a jiných povrchů. Nejčastěji jsou pro tyto účely používány trojúhelníky s proměnlivou velikostí a tvarem, tzv. nepravidelné trojúhelníkové sítě (triangular irregular network - TIN).

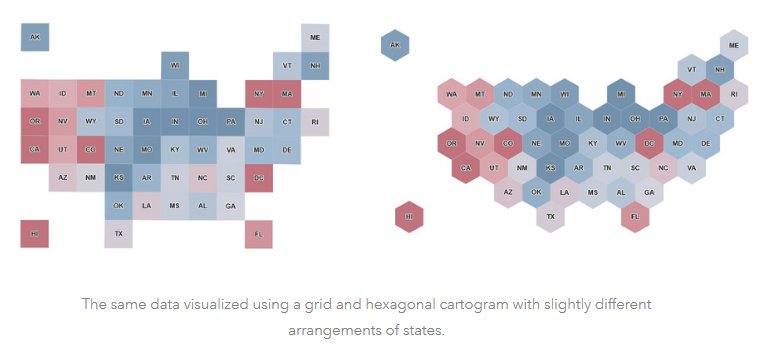
Obrázek 6: Čtvercový a hexagonální rastr (zdroj: https://twitter.com/GIS_Bandit/)

Topologie rastrových buněk je implicitně definována v geometrii rastru. Každý pixel má dva druhy sousedů:

• plné - dokonalé (full) sousedy - sousední pixely ve stejných řádcích nebo sloupcích - tyto buňky vytvářejí tzv. čtyřčlenné sousedské okolí (von Neumannovo);
• diagonální sousedy - pixely, které s daného dotýkají v jeho rozích;
• Obě skupiny sousedů vytvářejí tzv. osmičlenné sousedské okolí (Moorovo).

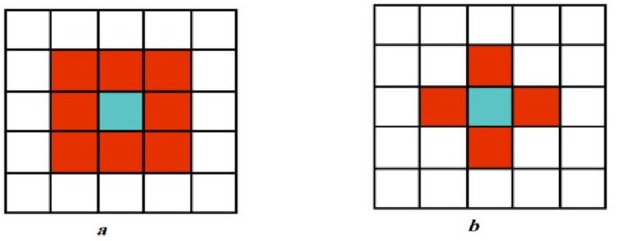
Obrázek 8: Moorovo (a) a von Neumanovo (b) okolí buňky (zdroj: Gazmeth et al., 2013)

4.1.1 Faktory ovlivňující kvalitu zobrazení reálného světa v rastru

Kvalitu zobrazení reálného světa pomocí rastrového datového modelu ovlivňuje několik faktorů:

• způsob přiřazení hodnot zobrazovaného atributu jednotlivým buňkám,
• prostorové rozlišení - velikost základní buňky rastru,
• barevné rozlišení - počet hodnot, kterých může pixel nabývat (záznam hodnot atributů), právně se nazývá v případě digitálního obrazu" radiometrickým rozlýšením v nápovědě ESRI je pak tento počet nazýván bitovou hloubkou angl. [Bit Depth].
  

Způsob přiřazení hodnot zobrazovaného atributu jednotlivým buňkám

Hodnoty atributu v jednotlivých buňkách mohou být stanoveny různými způsoby:

• jako bodová hodnota změřená kdekoliv v ploše buňky,
• jako aritmetický průměr z několika bodových měření,
• jako vážený aritmetický průměr, kde váhou je plošný rozsah jednotlivých hodnot,
• jako maximální nebo minimální hodnota atributu,
• jako hodnota atributu s nějvětší váhou.

Volba konkrétního způsobu přiřazení hodnot daného atributu jednotlivým buňkám může i výrazně ovlivnit výslednou reprezentaci zájmové oblasti v rastu, a to jednak co do průběhu hranic s různou hodnotou sledovaného atributu, i co do rezprezentace především malých oblasti.

Obrázek 9 ukazuje možné způsoby přiřazení hodnot buňce v případě, že do dané buňky zasahuje více kategorií land use.

Obrázek 9: Problém přiřazení hodnoty buňce s výskytem více kategorií

Velikost základní buňky rastru

Obecně platí: čím je základní buňka rastru menší, tím lépe (přesněji) lze v tomto rastru zachytit průběh hranic jednotlivých geoprvků (obrázek 10). Platí však také: zmenšením délky strany základní buňky rastru na polovinu se čtyřnásobně zvýší nároky na paměťový prostor, nezbytný k uložení rastru.

„Barevná hloubka“ (rozlišení) rastru

Při práci s rastry používáme pro záznam hodnot sledovaného atribut v jednotlivých buňkách různé rozlišení. Podle použitého rozlišení rozlišujeme následující typy rastrů:

• binární – zaznamenává se pouze přítomnost, resp. nepřítomnost atributu (nejčastěji hodnoty 0 a 1) – pro záznam hodnoty jedné buňky potřebujeme vždy jeden bit - např. naskenované katastrální mapy.
• osmibitový – v buňce rozlišujeme 256 různých celočíselných hodnot sledovaného atributu – pro záznam hodnoty jedné buňky rastru potřebujeme 1 Byte - např. naskenované barevné předlohy, panchromatické letecké a družicové snímky.
• čtyřiadvacetibitový – v buňce se rozlišuje cca 1.6 milionu různých celočíselných hodnot sledovaného atributu – pro záznam jedné buňky potřebujeme 3 Byte - např. multispektrální družicové snímky.
• kontinuální – v buňce rozlišujeme téměř neomezené množství reálných hodnot sledovaného atributu – pro záznam jedné buňky potřebujeme obvykle 4, resp. 6 Byte.

V praxi jsou nejčastěji využívány první tři typy rastrů. Binární rastry se používají při práci s naskenovanými katastrálními mapami, zdrojem osmibitových rastrů jsou především skenované barevné předlohy a panchromatické letecké a družicové snímky, případně jsou produkované rastrovými systémy při běžných rastrových analýzách. Čtyřiadvacetibitové rastry vznikají nejčastěji jako produkt zpracování multispektrálních družicových snímků.

4.2 Kvalitativní a kvantitativní rastry a rastrové formáty

Kvantitativní rastr znázorňuje kvantitu sledovaného jevu. Popisuje tedy velikost jevu zaznamenaného v dané buňce. Buňky mohou nabývat hodnoty typu reálné číslo. Hodnoty používané v kvantitativním rastru bývají z poměrové nebo intervalové domény. Pro tento typ rastrů je typická velká variabilita hodnot. Příklady kvantitativních rastrů jsou uvedeny na obrázcích 3. Většina programových aplikací pro GIS ma svůj vlastní natívní formát pro ukládání tohoto typu rastru.

Formáty pro ukládání kvantitativních dat: TIFF, GeoTIFF, BIL, BIP, BSQ, ArcInfo Grid (Binary, ASCII), RST (IDRISI), IMG (Erdas Imagine), GRD (Intergraph Raster Format).

Kvalitativní rastr vyjadřuje kvalitu (typ, druh, třídu, kategorii) jevu. Buňky nesou celočíselnou hodnotu. Většinou může být tato hodnota jen kladná, ale není to bezpodmínečným pravidlem. Hodnoty buněk používané v těchto rastrech jsou z výčtové (nominální) domény. Variabilita hodnot v tomto rastru je poměrně malá, zřídka kdy překročí v počtu hodnot první 100-vky hodnot.

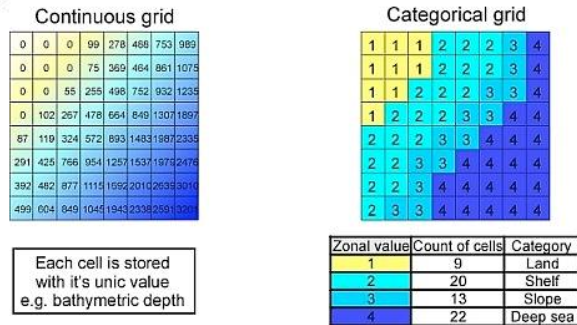
Obrázek 11: Kvantitativní a kategoriální rastr (zdroj: https://is.muni.cz/el/1431/jaro2017/Z0262/um/geoinformatika_03_fin.pdf)

U kvantitavních rastrů je možné provést rozdělení na rastry, které reprezentují tématická data, skutečně výčtové hodnoty například typ užití území, a rastry typu obrazový záznam , který se používá pro ukládání družicových dat, dat z leteckého snímkování, skenovaných meziproduktů, popřípadě k ukládání map.

Data typu image se v oblasti Geoinformatiky často používají jako topografický podklad nebo jako zdroj pro další následné zpracování, například do podoby tématických rastrů nebo kvantitativních rastrů. Příkladem rastru typu Image může být: letecký snímek, družicový záznam, nebo digitální rastrová kopie analogové mapy. Tato data jsou buď zobrazována jako třikanálová (RGB) s tím, že samotné soubory mohou obsahovat i desítky až stovky pásem.

Formáty pro ukládání obrazových dat: TIFF, JPEG, PNG, BMP, MrSID, ECW, BIL, BIP, BSQ + proprietární formáty výrobců uvedené u kvantitativních rastrových dat.

4.3 Triangulace

Z určitého souboru vstupních bodů lze vytvořit velké množství trojúhelníkových sítí. Tato procedura se nazývá triangulace. Velký význam má tzv. Delaunay triangulace (viz obrázek 12). Triangulace je Delaunay triangulací právě tehdy, když do kružnice opsané každému z trojúhelníků nepadne žádný jiný bod. Vrchol každého trojúhelníku sítě je ohraničen konvexním trojúhelníkem.

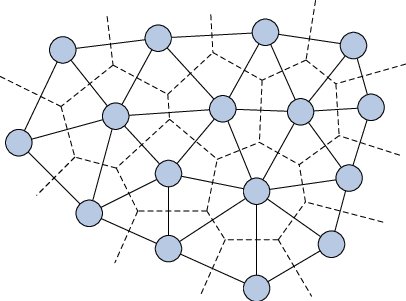
Obrázek 12: Delaunay triangulace a Voronoi diagram (zdroj: DalleMole et al., 2010)

Dualita této triangulace se nazývá Voronoi diagram nebo Thiessenovy polygony či Dirichlet tesselace. Vrcholy Voronoi polygonů jsou zároveň středy kružnic opsaných Delaunay trojúhelníkům. Kolmice vedené ke středům stran Delaunay triangulace vytvářejí hrany Voronoi polygonů. Vzhledem k tomu, že Delaunay triangulace a Voronoi polygony tvoří dualitu, lze vytvářet Delaunay triangulaci z Voronoi polygonů a naopak. Požadavek “nepřítomnosti bodu v kružici opsané trojúhelníkům sítě” se nazývá kritériem prázdné kružnice nebo Delaunay kritériem.

Pokud definujeme buňku rastru jako nedělitelnou základní jednotku prostoru, rastrový model dále nepotřebuje souvislý souřadnicový systém. Úplně postačí diskrétní rastrový prostor. V důsledku toho nepotřebujeme pro popis polohy v rastru dvojice souřadnic. K definování polohy buňky vzhledem k počátku rastru postačí dvojice indexů \(i,j\). Zavedeno je použití indexu j jako indexu řádků buněk rastru a indexu i jako indexu slupců buněk rastru. V porovnání s vektorovým modelem je tento typ popisu polohy velmi jednoduchý. Namísto reálných souřadnic používáme celočíselné proměnné jako indexy. Tato skutečnost je velmi důležitá z hlediska potřebného paměťového prostoru.

Indexy můžeme vypočítat ze souřadnic podle následujících pravidel:

\(X_{1}\rightarrow i=0\)

\(Y_{1}\rightarrow j=0\)

\(X=X_{1}+p\cdot \delta X \rightarrow i=p\)

\(Y=Y_{1}+q\cdot \delta Y \rightarrow j=q\),

kde \(\delta X\), \(\delta Y\) jsou velikosti krokové vzdálenosti (rozměry základní buňky rastru), které určují rozlišovací schopost (resolution) rastru. Jejich zmenšování způsobuje zvyšování rozlišovací schopnosti. Souřadnice z indexů lze vypočítat opačným použitím výše uvedených pravidel.

Doba zpracování v případě většiny operací na rastrech závisí na jejich rozlišovací schopnosti, více méně narůstá s objemem zpracovávaných údajů. Proto je nezbytné správně odhadnout rovnováhu mezi detailností popisu prostoru a objemem příslušných dat. Star a Estes definují délku strany buňky nebo velikosti kroku, která definuje rozlišovací schopnost rastru jako polovinu nejmenší délky, která je potřebná k reprezentaci objektů existujících v reálných podmínkách. Toto pravidlo lze nazvat jako “pravidlo minimální kartografické délky”.

4.4 Metriky rastrové reprezentace dat

V rastrech jsou nejčastěji používány tyto metriky:

• metrika hran (bloková metrika) - vzdálenost dvou buněk je definována jako minimální počet překonaných hran buněk (obrázek 13), někdy také označována jako Manhatanovská metrika;

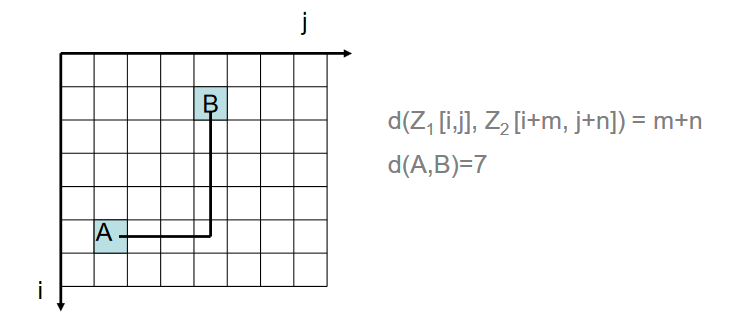
Obrázek 13: Bloková metrika

• metrika hran a středů (šachovnicová metrika) - vzdálenost dvou buněk je definována jako minimální počet překonaných hran nebo středů (přípustný je tedy i úhlopříčný směr pohybu),

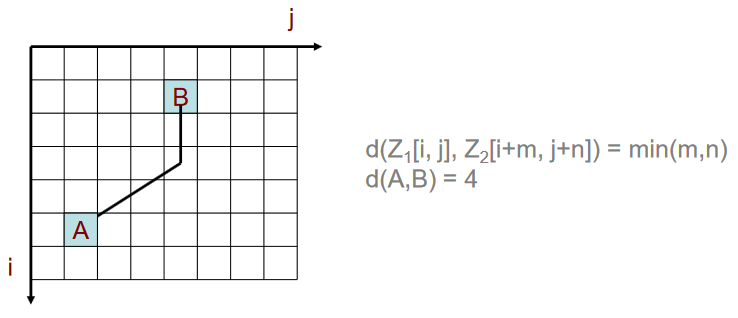
Obrázek 14: Šachovnicová metrika

• Euklidovská metrika - poloha každé buňky je reprezentována polohou jejího středu, vzdálenost mezi buňkami je pak definována jako vzdálenost jejich středů (obrázek 15).

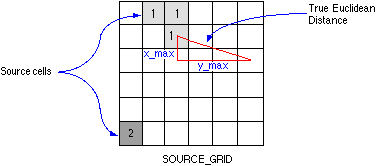
4.5 Datové struktury používané pro ukládání rastrových dat - metody komprese údajů

Pro ukládání rastrových dat jsou používány různé datové struktury. Tou nejjednodušší je ukládání rastrových dat po buňkách, nejčastěji v textovém souboru, kde jsou vždy na řádku tři údaje: řádkový a sloupcový index (resp. souřadnice \(i,j\), případně \(x,y\)) a hodnota reprezentovaná buňkou. Tento způsob je z hlediska nároků na diskový prostor nejméně výhodný. Jeho použití je však někdy nevyhnutelné, pokud potřebujeme přenést rastrová data mezi dvěma zcela nekompatibilními systémy.

Jinou možností je ukládání rastrových dat v podobně matice. Hlavní nevýhodou této reprezentace je značný nárok na paměť, další nevýhodou je také to, že k uloženým datům je nezbytné připojit i doprovodné údaje, které uživatele informují např. o rozměrech rastru (počtu buněk na řádku, počtu řádků), rozlišení dat v buňce (binární, osmibitové, čtyřiadvacetibitové apod.), způsobu uložení (po řádcích, po sloupcích, po segmentech, resp. dlaždicích (tile)), o tvaru základní buňky, jejích reálných rozměrech, případně o úhlu, který svírají osy \(i\) a \(j\) (resp. \(x\) a \(y\))(v případě kosého tvaru buňky), případně o poloze rastru v referenčním polohovém systému a dále parametry nezbytné pro transformaci rastru do tohoto referenčního systému.

Při přímém datování každé buňky nebo přímém datování informační vrstvy je tedy možné výrazně redukovat objem uložených dat vyloučením jejich souřadnic nebo indexů v systému řádků a sloupců rastru. V datovém souboru se uloží jen obsah jednotlivých buněk a jejich polohu lze identifikovat na základě údajů zvláštního souboru, ve kterém jsou definovány prostorové parametry datového souboru (min. a max. hodnoty souřadnic zkoumaného území, počet řádků a sloupců rastru, velikost buňky atd.). Takový způsob používá např. systém IDRISI. Tyto parametry nemusí tvořit vždy samostatný soubor, mohou být obsaženy i v datovém souboru - v jeho úvodní části, tzv. hlavičce (header).

V nejjednodušším případě je možné si představit přepis matice hodnot rastru do řady - seznamu hodnot buněk po řádcích nebo sloupcích (row order), resp. zpětně po řádcích nebo sloupcích (row-prime order) - viz obrázek 16. Toto je také nejčastěji používaný přístup (obrázek 17).

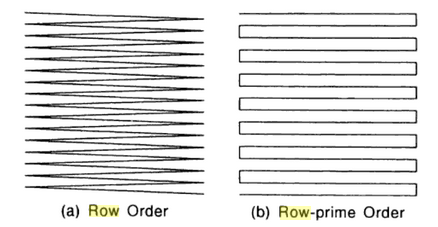
Obrázek 16: Schéma ukládání rastru po řádcích nebo zpětně po řádcích (zdroj: Bonham-Carter, 2013)

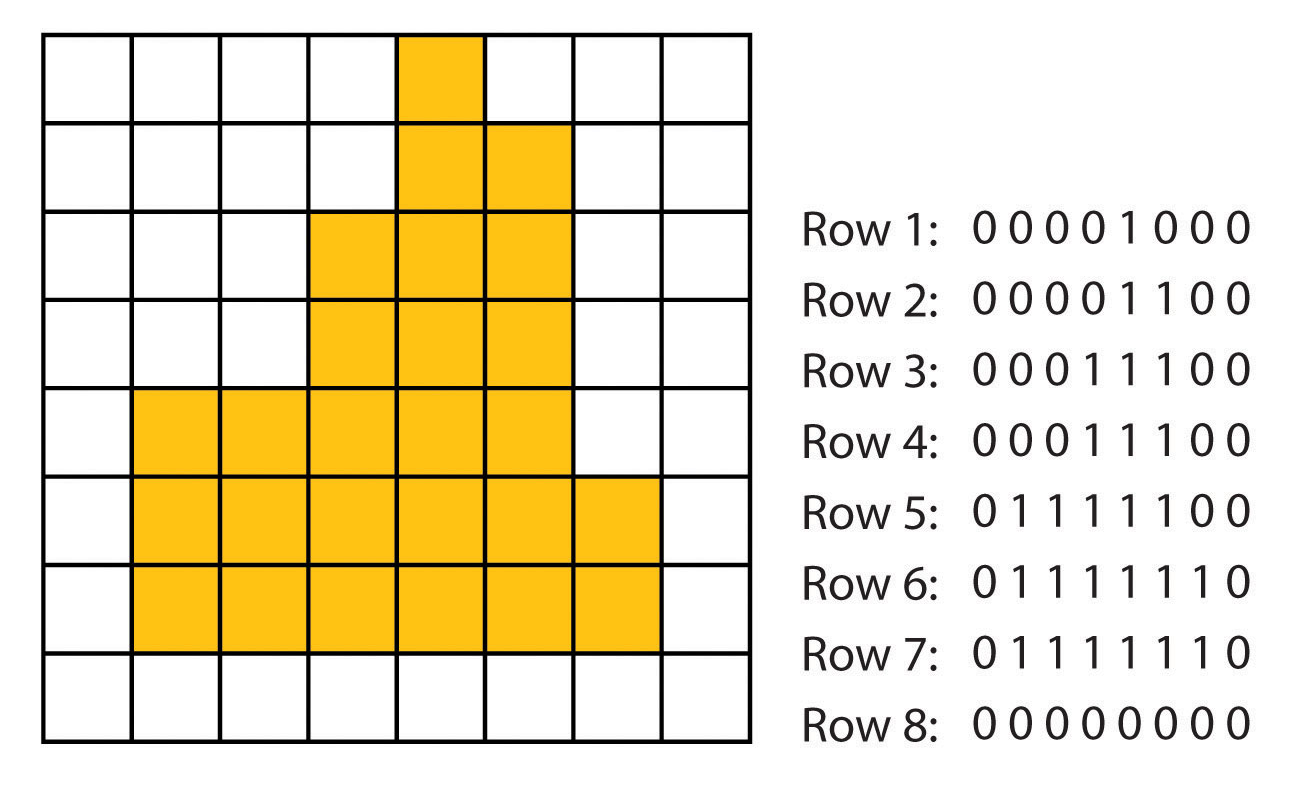
Obrázek 17: Ukládání rastru po řádcích (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-01-raster-data-models.html)

Běžně se stává, že v takto vytvořeném pořadí se opakuje více stejných hodnot, uložených v buňkách jdoucích za sebou. Z toho vychází jeden z nejjednodušších a také nejčastěji používaných způsobů komprese údajů, tzv. metoda délkových kódů (run-length encoding), při které jsou originální hodnoty údajů z buněk pořadí nahrazeny tzv. tupples, které jsou tvořeny dvojicemi čísel: první udává uloženou hodnotu a druhé počet jejích opakování v pořadí (obrázek 18).

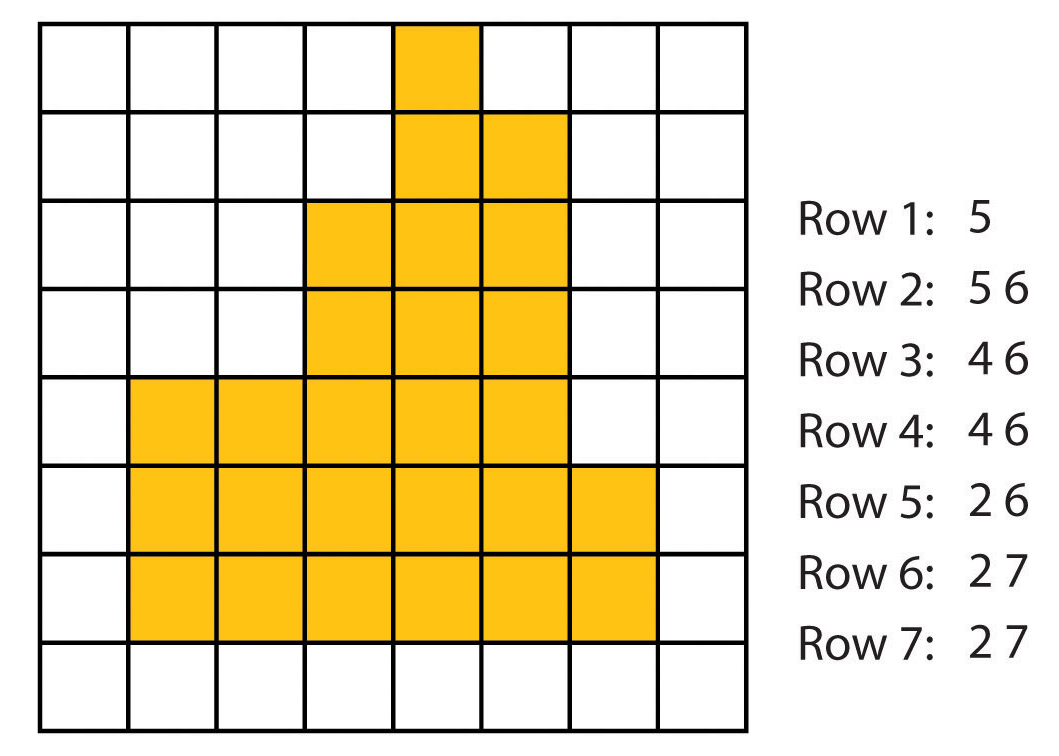
Obrázek 18: Run-length encoding (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-01-raster-data-models.html)

Další možnosti stanovení pořadí hodnot rastru, podle kterého budou přepisovány z údajové matice do souboru:

• Mortnovo pořadí - používá se u rastrů, jejichž rozměry (počet řádků a sloupců) jsou dělitelné 4 a jsou stejné. Je to “cik-cak” pohyb začínající v levém dolním rohu, vytvářející podobu obráceného písmena Z u čtyř buněk (obrázek 19). Tento pohyb se opakuje i na vyšších hierarchických úrovních. Mortnovo pořadí je používáno při metodě délkových kódů jako “způsob vyplnění prostoru” při čtení hodnot rastru. Na rozdíl od pořadí po řádcích se zde stanou blízkými v pořadí i prvky blízké si navzájem v prostoru (ploše), což má velký význam pro některé analýzy.

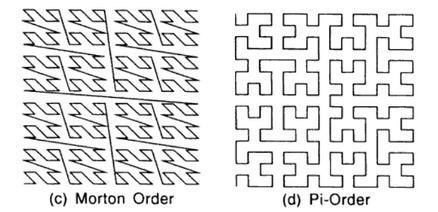
Obrázek 19: Mortnovo a Peanovo pořadí (zdroj: Bonham-Carter, 2013)

Další zajímavostí Mortnova pořadí (obrázek 20) je, že pokud dodržíme číslování řádků a sloupců od 0 a jejich počet bude dělitelný 2, je možné využít binární adresování (bit interlaving) pro stanovení polohy buňky v systému řádků a sloupců rastru na základě jejího postavení v řadě hodnot, vytvořených pomocí Mortnova pořadí.

Obrázek 20: Binární adresování (zdroj: https://gistbok.ucgis.org/bok-topics/origins-computing-and-gist-part-2-perspective-role-peripheral-devices)

• Další “křivkou vyplňující prostor” je Peano křivka nebo Peano pořadí (Pi-Order na obrázku 19). V porovnání s Mortnonovým pořadím jsou změny směru pravoúhlé, ostatní výhody si zachovává.

Při přímém datování objektů lze použít více tzv. vylepšených postupů uložení rastrových dat:

• Řetězcové kódy (chain codes) - definují hranice každého polygonu kódováním směru (orientace) průběhu hranice od zadaného východiskového bodu (obrázek 21). Nevýhodou tohoto postupu je vícenásobné uložení úseků hranice společných více polygonům.

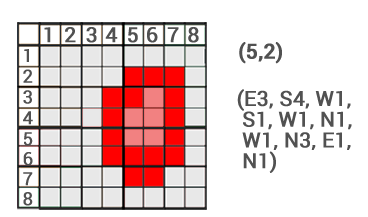
Obrázek 21: Řetězcové kódy (zdroj: https://gisgeography.com/image-compression-encoding/)

• Blokové kódy (block codes) - udávají polohu referenčních bodů a velikost čtvercových bloků, ze kterých je možno vytvořit celý objekt (obrázek 22).

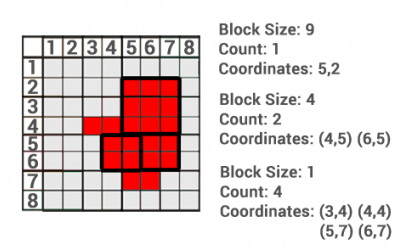
Obrázek 22: Blokové kódy (zdroj: https://gisgeography.com/image-compression-encoding/)

• Kódování úseků řádků (run lenght codes) - definuje příslušnost buněk rastru k objektu po řádcích nebo sloupcích, přičemž udává jen začátek a konec úseku buněk v systému řádků a sloupců, které mají uloženou stejnou hodnotu (obrázek 23). Někteří autoři označují tento postup také “standard run-lenght codes” (Aronof, 1989).

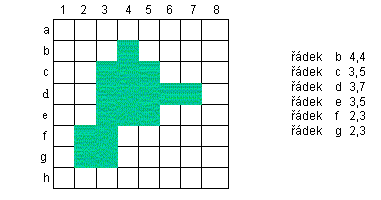
Obrázek 23: Kódování úseku řádků

• Kódování metodou čtyřstromu (quadtree) - je založeno na postupném pravidelném dělení rastru na kvadranty a subkvadranty tak dlouho, až je buď v celém kvadrantu stejná hodnota sledovaného atributu nebo je dosaženo nejmenšího možného rozměru kvadrantu (rovného rozměru základní buňky). Cílem tohoto modelu je mít možnost použít lepší prostorové rozlišení pro popis krajiny v těch místech, kde je potřeba většího detailu a přitom nezvyšovat objem databáze tím, že se zvětší velikost pixelu v místech homgenních. Rozdělení pixelu na čtvrtiny následuje vždy po zjištění, že se v jeho vnitřku nachází více než jedna třída (obrázek 24). Z kartografického hlediska se jedná o model proměnného měřítka se změnou vyjádřenou mocninou dvou, který je kompatibilní s konvenčním kartézským systémem souřadnic.

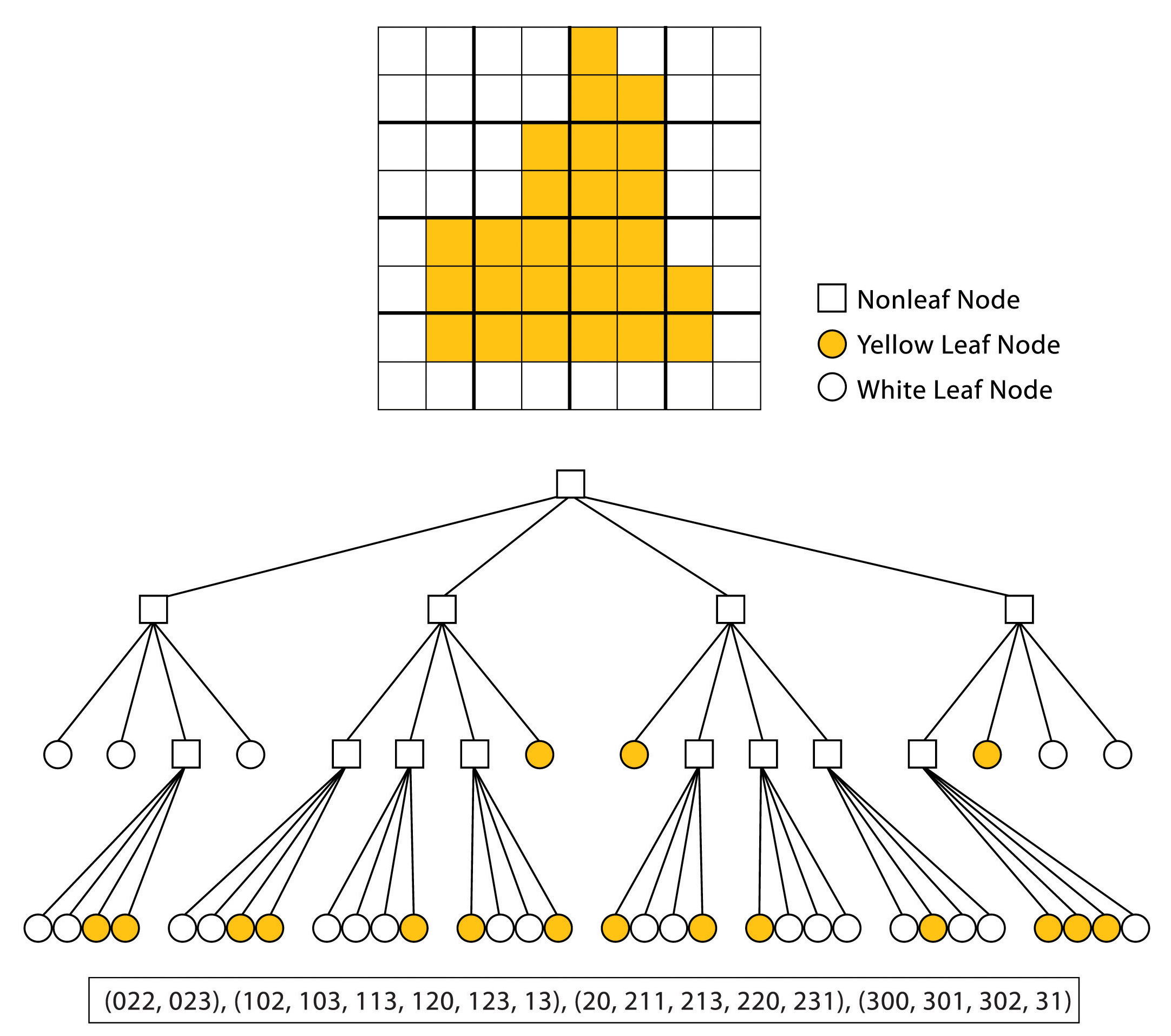
Obrázek 24: Čtyřstrom (zdroj: https://saylordotorg.github.io/text_essentials-of-geographic-information-systems/s08-01-raster-data-models.html)

Podobný postup lze aplikovat i na trojrozměrný prostor, prostorovými elementy se pak stávají krychle a vytváříme tzv. osmstrom (octtree).

V praxi byla navržena celá řada datových struktur, umožňujících reprezentaci quadtree v paměti počítače. K nejpoužívanějším patří tzv. lineární quadtree, ve kterém jsou zaznamenány jen koncové uzly (listy), každý uzel je označen speciálním numerickým klíčem, z něhož lze snadno odvozovat prostorové vztahy. Tento princip je využíván např. v rámci softwarového produktu SPANS firmy Tydac Technologies.

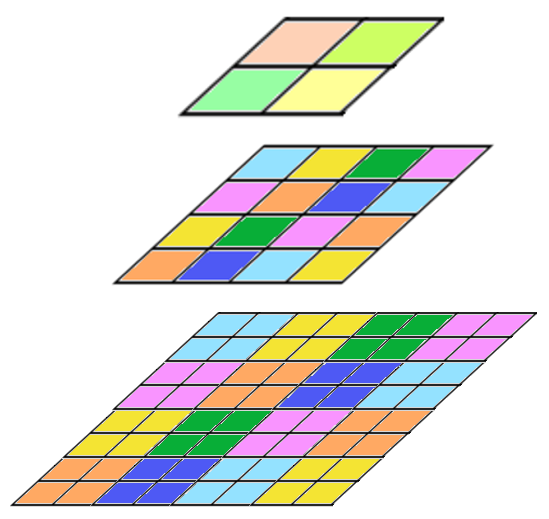
Jinou hierarchickou datovou strukturou je pyramida, která na rozdíl o quadtree ukládá všechny buňky v hierarchii, přičemž hodnota reprezentovaná ve vyšších buňkách je obvykle stanovena jako průměrná hodnota z buněk ležících o jednu úroveň níže (obrázek 25). Postupujeme tak, že si nejprve zobrazíme rastr ležící na nejvyšší úrovni, který má největší rozměr základní buňky a tím i nejmenší rozlišení. V tomto rastru snadno nalezneme oblast, která nás zajímá. Pak se přepneme do rastru, ležícího o úroveň níže a provedeme přesnější lokalizaci zájmové oblasti. Opět se přepneme do rastru s menším rozměrem základní buňky, který zobrazuje zájmovou oblast mnohem detailněji. Tyto kroky opakujeme tak dlouho, až dosáhneme rastru ležícího na nejnižší úrovni pyramidy, který zobrazuje zájmové území nejdetailněji.

4.6 Zhodnocení rastrového datového modelu

Z pohledu realizace jednotlivých složek popisu geoprvků je na tom rastrový model nejhůře (Rapant, 2002). Většina přoblémů vzniká proto, že v rastrovém modelu nelze pracovat přímo s jednotlivými geoprvky, ale pouze s rastry, znázorňujícími rozložení vlastností geoprvků v zájmové oblasti:

• geometrická složka je obsažena v tomto modelu pouze implicitně, explicitní vyjádření je prakticky nemožné,
• tematická složka je realizována v podobě jednotlivých rastrů, znázorňujících rozložení vlastností v zájmové oblasti,
• časovou složku je možné zachytit jen jako posloupnost rastrů, znázorňujících rozložení stejného atributu v různých časových okamžicích,
• vztahovou složku lze realizovat pouze omezeně, v rozsahu odpovídajícím možnostem rastru,
• funkční složku je možné realizovat v podobě programů, zpracovávajících rastry.