Kapitola 8 Geografická poloha, restrukturalizace dat

Ze studia zeměpisu na základních a středních školách máme přibližnou představu o tvaru naší planety Země a o jejím okolí. V této kapitole zavedeme bližší pojmy popisující její tvar a způsob určování polohy na jejím povrchu. Moderní GIS nástroje sice umožnují jisté formy zpracování trojrozměrné reality, ale v našich aplikacích budeme výhradně mluvit o dvojrozměrném přístupu k prostoru – tedy výhradně o popisu povrchu Země.

Evolucí planety Země vznikl povrch pomerně hodne zvrásněný a členitý. Dovedeme si představit jednoduchost matematického popisu povrchu koule nebo rotačního elipsoidu, od které se rozhodně reálný tvar naší planety hodne liší. Každý bod Země muže být předmětem geodetického zkoumání. Potřebujeme proto jistou formu zjednodušení, která by vedla na univerzální mapování reálného povrchu Země na plochu mapy (na papír).

Zavádí se postupné zjednodušování popisu tvaru zemského tělesa. Počáteční aproximací – tedy vlastně modelem – je tak zvaný geoid. Vycházíme z idealizované plochy zemského povrchu, která byla definována jako plocha, kde v každém jejím bodě má zemská tíže stejnou hodnotu. Tuto plochu pokládáme na úroveň klidné střední hladiny moří (která rozhodně také není stabilní). Tím pádem fakticky zasahuje pod povrch pevniny. V jistém smyslu povrch geoidu představuje úroveň nadmořské výšky nula metrů. Samotný údaj nadmořské výšky je jaksi diskutabilní - moře se totiž přelévá v procesech známých jako příliv a odliv (slapové jevy). Střední hladina je průměr výšky mezi přílivem a odlivem (výškový rozdíl v Atlantiku muže být víc než pět metrů). Nadmořská výška v oblasti Evropy se obvykle vztahuje k Baltskému moři.

Přistupme k definici geoidu:

Geoid je myšlená nulová hladinová ekvipotenciální plocha, která je v každém bode kolmá na směr zemské tíže.

Obrázek 1: Geoid (zdroj: https://www.abicko.cz/clanek/precti-si-technika-vesmir/22531/sisata-planeta-skutecna-podoba-zeme.html)

Typický tvar geoidu si můžeme ukázat na obrázku 2. Hnědá čára ukazuje skutečný povrch Země, modrá čára plochu geoidu a černá plochu náhradního elipsoidu. Vidíme, že ani geoid není jednoduše matematicky popsatelný. V podstatě jenom poněkud vyhladil zvrásněný skutečný topografický povrch. Proto se zavádí další model geoidu a tím je náhradní elipsoid. Náhradní elipsoid je již počátek kartografie.

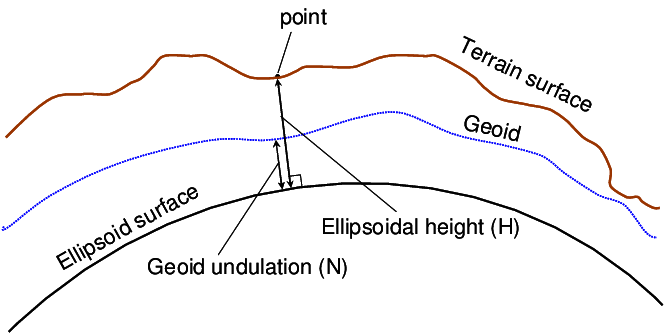
Obrázek 2: Geoid a zemský porvrch (zdroj: Ziebart et al., 2004)

Plocha geoidu je sice v jistém smyslu ideální, ale i přesto se matematicky obtížně popisuje. Je to zřejmé z předchozího obrázku. Proto se zavádí další priblížení a tím je rotační elipsoid. Rotační elipsoid je známý geometrický objekt, který je dán svým středem a délkami kratší a delší poloosy. Jde o tzv. dvouosý elipsoid, který vzniká rotací elipsy kolem vedlejší poloosy. Lze jej vyjádřit rovnicí:

\(\frac{x^{2}+y^{2}}{a^{2}}+\frac{z^{2}}{b^{2}}=1\)

Pro upřesnění: v matematické kartografii je používán výhradně dvouosý elipsoid. Existují dva způsoby aproximace zemského povrchu a s nimi související výsledné typy elipsoidů:

zemský elipsoid - vzniká aproximací geoidu, střed má totožný s hmotným středem Země (geocentrem), malá osa je totožná se středem rotace.
referenční elipsoid - vzniká aproximací části geoidu, střed není totožný se středem Země, na vybrané území aproximuje lépe než zemský elipsoid, zobrazení definovaná na rotačním elipsoidu vykazují menší zkreslení než zobrazení definovaná na zemském.

Obrázek 3: Referenční elipsoid (zdroj: https://cs.wikipedia.org/wiki/Referenční_elipsoid)

V oborech příbuzných GIS se rotační elipsoid tedy nejčastějí nazývá referenční (náhradní) elipsoid. Tento elipsoid lze zadávat různým způsobem – volíme parametry délky kratší a delší osy. Ruzné volby elipsoidu nahrazují geoid s různou přesností (pravdivostí), poněvadž se na ruzných místech geoidu elipsoid jinak přimyká (mění se vzdálenost plochy geoidu od elipsoidu). Volba náhradního elipsoidu je tedy věcí jistého kompromisu, platného obvykle jenom na menších územích (národní elipsoidy). Volba náhradního elipsoidu pro konkrétní použití se v anglické literature nazývá datum.

Pro účely větších mapových děl je nezbytné data vztahovat vzhledem ke globálnímu elipsoidu, který by postihoval celou planetu. Globální elipsoid se vyvíjel dlouhou dobu a ustálil se až v roce 1984 v podobě nazvané WGS-84. Jeho použití je však pro účely národní geodézie nevhodné. Parametry nejznámějších elipsoidů ukazuje obrázek 4.

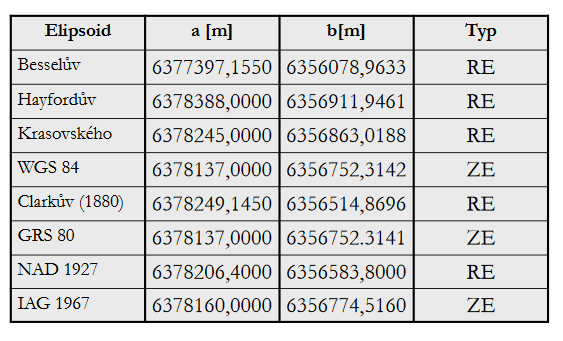
Obrázek 4: Nejznámější elipsoidy (zdroj: https://web.natur.cuni.cz/~bayertom/images/courses/mmk/mk0.pdf)

Referenční elipsoid může být pak nahrazen jednodušším tělesem, a to referenční koulí, která má jednodušší matematickou definici. Referenční koule má větší odchylky od geoidu než elipsoid. Její poloměr \(R\) lze volit různými způsoby a má následující vlastnosti:

konstatní křivost,
provádějí se na ní snadněji výpočty,
je vhodná pro mapy malých a středních měřítek (nikoliv státní mapové dílo).

Referenční kouli (obrázek 5) lze nahrazovat:

elipsoidem lokálně (území 300 x 300 km) - přesné výpočty na malém území (lze zanedbat rozdíly),
elipsoidem globálně - méně přesné výpočty na celém povrchu Země - využití v geografické kartografii.

Kartografická zkreslení při nahrazení geoidu koulí jsou o 2 řády (100x) větší než při nahrazení geoidu elipsoidem.

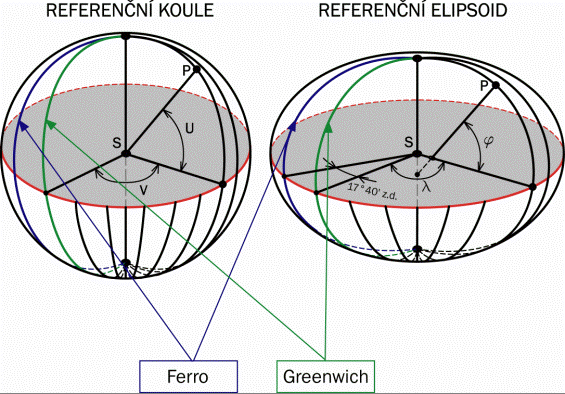
Obrázek 5: Referenční koule a referenční elipsoid (zdroj: http://gisak.vsb.cz/GISacek/GISacek_2001/sbornik/Hanzlova/Hanzlova.htm)

Při náhradě elipsoidu koulí na malém území můžeme její poloměr \(R\) volit následujícími způsoby:

\(R=a\),
\(R=b\),
\(R\) je střední poloměr křivosti \(R=\sqrt{MN}\).

Náhradu elipsoidu globálně lze provést těmito způsoby:

Kolule bude mít stejný objem jako elipsoid, \(R=\sqrt[3]{a^{2}b}\);
Koule bude mít stejný povrch jako elipsoid, \(R=b\sqrt{(1+\frac{2}{3}e^{2}+\frac{3}{5}e^{4}+\frac{4}{7}e^{6}\dots)}\);
Průměr koule je vyjádřen jako aritmetický průměr poloos: \(R=\frac{2a+b}{3}\).

Při tvorbě dvourozměrné mapy je pak potřeba převést obraz z trojrozměrné předlohy (referenčního elipsoidu či referenční koule) do roviny. Plocha, na kterou zobrazujeme objekty z referenční plochy, se nazývá zobrazovací plocha. Nejčastěji používané plochy rozvinutelny do roviny jsou kuželová, válcová či tečná rovina. Lze zobrazovat na více než jednu plochu (polykónická zobrazení).

8.1 Geografická poloha

Dříve než můžeme pracovat s geoprvky, musíme jednoznačně definovat jejich polohu v prostoru. K tomuto účelu můžeme použít celou řadu různých tzv. prostorových referenčních systémů (obrázek 6), popisujících polohu geoprvků různými způsoby, s různou přesností a s různým rozlišením.

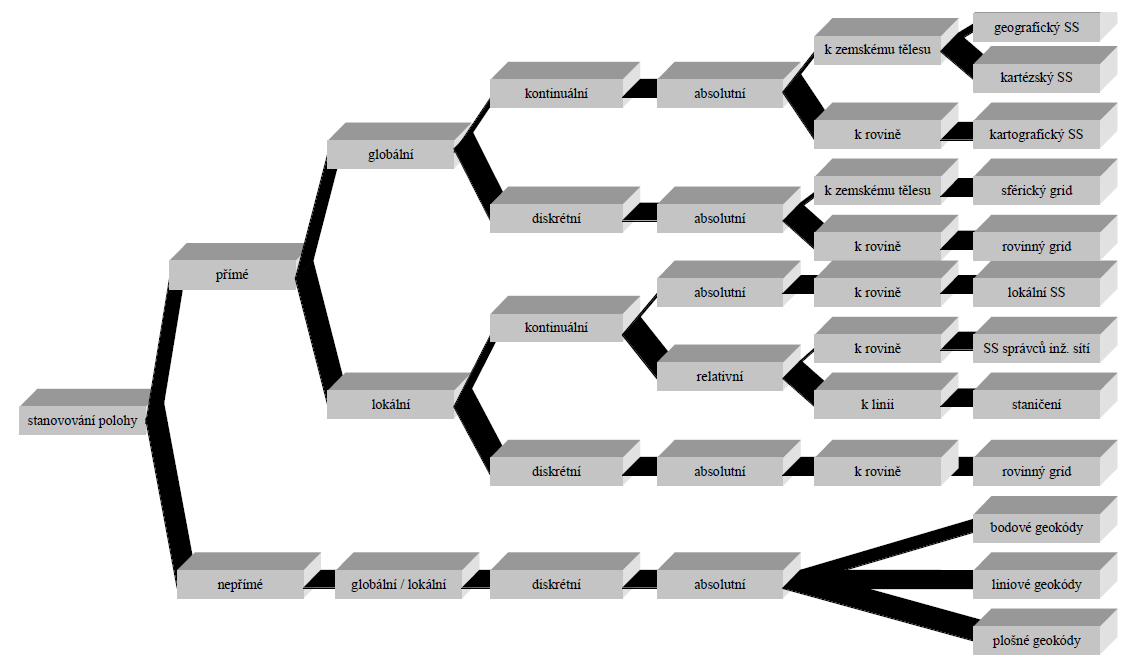
Obrázek 6: Prostorové referenční systémy (zdroj: Rapant, 2002)

Polohu je možné určovat v zásadě dvěma způsoby:

přímo pomocí souřadnicových systémů (anglicky georeferencing),
nepřímo pomocí geokódů (anglicky geocoding).

8.1.1 Přímé stanovování polohy (georeferencing)

V případě přímého stanovování polohy pomocí souřadnicových systémů rozlišujme:

globální souřadnicové systémy,
lokální souřadnicové systémy.

8.1.1.1 Globální souřadnicové systémy

Globální souřadnicové systémy jsou taové, které se používají pro stanovování polohy v rámci velkých areálů (celá Země, stát nebo alespoň velká část státu). Z hlediska plynulosti stanovování polohy se globální souřadnicové systémy dělí na:

kontinuální souřadnicové systémy,
diskrétní souřadnicové systémy.

Globální kontinuální souřadnicové systémy

Kontinuální souřadnicové systémy jsou založeny na kontinuálním měření polohy geoprvků, bez skokových změn souřadnic a přerušování. Lze je podle způsobu odvozování polohy geoprvků dále dělit na:

absolutní,
relativní.

vzhledem k tomu, že relativní stanovování polhy se v případě globálních systémů prakticky nepoužívá, budeme se dále věnovat pouze varinatě absolutní, kdy je poloha dána přímo souřadnicemi vyjádřenými v globálním souřadnicovém systému.

Tyto souřadnicové systémy mohou být definovány ve vztahu k:

zemskému tělesu,
k rovině, do níž je zemský povrch promítnut.

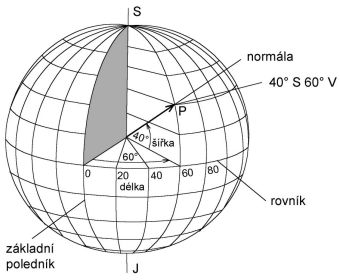
Obrázek 7: Geografický souřadnicový systém (zdroj: http://tvorbamap.shocart.cz/kartografie/projekce.htm)

Obvykle jsou uváděny dva základní souřadnicové systémy vztažené k zemskému tělesu:

geografický souřadnicový systém (v principu sférický) - poloha bodu na zemském povrchu (obrázek 7) je dána pomocí zeměpisné šířky \(\varphi\) (anglicky latitude) a zeměpisné délky \(\lambda\) (anglicky longitude). Zeměpisná délka se udává ve stupních, nula stupňů odpovídá Greenwichskému (nultému) poledníku. Zeměpisná šířka se udává také ve stupních, nula stupňů odpovídá rovníku, \(90^{o}\) odpovídá pólům. Geografické souřadnice se někdy doplňují ještě nadmořskou výškou \(h\), udávanou v metrech.
kartézský souřadnicový systém s počátkem ve středu Země (obrázek 8), udává polohu bodu pomocí trojice souřadnic \([x,y,z]\). Osy \(x\) a \(y\) leží v rovině rovníku, osa \(x\) prochází průsečíkem nultého poledníku a rovníku, osa \(z\) je k nim kolmá a obvykle totožná s osou rotace Země.

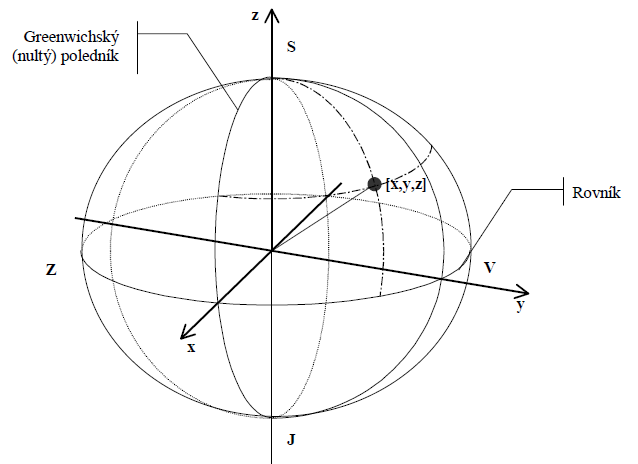
Obrázek 8: Kartézský souřadnicový systém (zdroj: Rapant, 2002)

Podstatnou odlišností těchto dvou systémů je skutečnost, že zatímco v případě geografického souřadnicového systému je poloha definována jen dvěma souřadnicemi a automaticky se předpokládá, že popisovaný bod leží na povrchu Země, tak v případě kartézského souřadnicového systému je poloha popsána třemi souřadnicemi. Výhodou kartézského souřadnicového systému je, že lze s jeho pomocí popsat polohu kteréhokoliv bodu, tedy i nad či pod povrchem Země.

Souřadnicové systémy vztahující se k rovině, do níž je povrch Země promítnut

Souřadnicových systémů patřících do této skupiny je celá řada a souvisí s kartografickými technikami, tj. znázorňováním povrchu Země na mapách. Chceme-li určitou velkou část zemského povrchu (kde již nelze zanedbat zakřivení) zobrazit na ploché mapě, musíme provést následující tranformace:

redukci měřítka tak, aby se zobrazovaná oblast vešla na list papíru požadované velikosti,
systematickým způsobem promítnout zakřivený povrch do roviny. Tomuto promítání se říká kartografické zobrazení a v podstatě se jedná o systematickou transformaci geografických souřadnic \((\varphi,\lambda)\) do odpovídajících rovinných souřadnic \((x,y)\) mapy. Matematicky lze tuto tranformaci zapsat takto:

\(x=f_{1}(\varphi,\lambda)\)

\(y=f_{2}(\varphi,\lambda)\)

a schematicky naznačit

\((\varphi,\lambda)\longrightarrow (x,y)\)

Tato transformace se obvykle skládá z několika kroků (jak již bylo zmíněno výše):

Transformace povrchu zemského na povrch geoidu. Povrch zeměkoule je příliš členity na to, aby s ním bylo možné efektivně pracovat. Proto se povrch Země zpravidla nahrazuje náhradní plochou, která se co nejtěsněji přimyká skutečnému průběhu terénu, ale nebere v úvahu nepodstatné detaily, jejichž vynechání výrazným způsobem neovlivní kvalitu výsledného díla.
Transformace povrchu geoidu na povrch dvojosého elipsoidu. Vzhledem k tomu, že geoid je zcela obecná plocha, je nezbytné nahradit ho jinou plochou, kterou lze matematicky snadno popsat a s kterou lze díky tomu snadno pracovat. K tomuto účelu se jako nejvhodnější ukázal rotační dvojosý elipsoid. Postupem času zavedli kartografové celou řadu elipsoidů, vhodných pro různé účely a pro zobrazení různých částí povrchu zemského (obrázek 4). Referenční elipsoid se používá při definici státních a mezinárodních geodetických souřadnicových systémů, při tvorbě mapových děl velkých a středních měřítek, kdy je vyžadováno minimální zkreslení.
Tranformace povrchu elipsoidu na povrch koule. Referenční elipsoid se nahradí referenční koulí. Někdy se referenční koule používá místo rotačního elipsoidu. To v případě, kdy máme nižší nároky na přesnost zobrazení, např. v případě tvorby map malých měřítek, např. nástěnných či atlasových.
Transformace povrchu koule na plochu rozvinutelnou do roviny (plášť válce, plášť kužele, tečná rovina).
Rozvinutí plochy do roviny a zavedení pravoúhlého souřadnicového systému.

Kartografických zobrazení dnes existuje široká škála. Např. v ČR se běžně používá kartografické zobrazení Křovákovo (a jemu odpovídající souřadnicový systém S-JTSK), které bylo vytvořeno speciálně pro bývalou Československou republiku a které respektovalo její protáhlý tvar a polohu na zemském glóbu.

Vláda ČR vydala Nařízení č. 430/2006 Sb.o stanovení geodetických referenčních systémů a státních mapových děl závazných na území státu a zásadách jejich používání, kterým stanovila závazné geodetické referenčn systémy pro území našeho státu:

Světový geodetický referenční systém 1984 (WGS84),
Evropský terestrický referenční systém (ETRS),
Souřadnicový systém Jednotné trigonometrické sítě katastrální (S-JTSK),
Katastrální souřadnicový systém gusterbergský,
Katastrální souřadnicový systém svatoštěpánský,
Výškový systém baltský -po vyrovnání (Bpv),
Tíhový systém 1995 (S-Gr95),
Souřadnicový systém 1942 (S-42/83).

V příloze tohoto nařízení jsou současně uvedeny i parametry těchto geodetických referenčních systémů.

Globální diskrétní souřadnicové systémy

Globální diskrétní souřadnicové systémy existují prakticky také jen ve verzi absolutní. Mohou být definovány opět ve vztahu k:

zemskému tělesu,
k rovině, do níž je zemský povrch promítnut.

Příkladem globálního diskrétního souřadnicového systému vztahujícícho se k zemskému tělesu, může být sférický grid (obrázek 9), který pokrývá povrch zeměkoule. Odvozuje se od oktaedru vepsaného do zeměkoule, jehož trojúhelníkové strany jsou postupně rozdělovány na menší a menší trojúhelníky s tím, že nově vygenerované vrcholy jsou přimknuty k povrchu zemskému (obrázky 10 a 11).

Obrázek 9: Sférický grid - základní oktaedr (zdroj: Rapant, 2002)

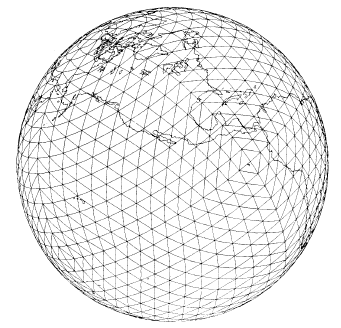
Obrázek 10: Sférický grid - ukázka výsledku po čtvrtém dělení (zdroj: Rapant, 2002)

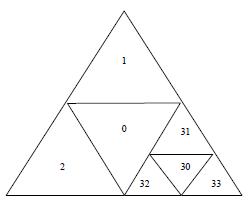
Obrázek 11: Sférický grid - ukázka dělení a adresace (zdroj: Rapant, 2002)

Souřadnicové systémy vztahující se k rovině, do níž je povrch Země promítnut

Tyto souřadnicové systémy se používají prakticky výhradně při práci s rastrovými daty. Je pro ně typické, že se souřadnice mění skokem. Poloha je definována pravidelně rozmístěnými plošnými prvky zpravidla čtvercového tvaru, odpovídajícími jednotlivým buňkám. V rámci rastru je obvykle používán lokální souřadnicový systém, jehož počátek leží zpravidla v levém horním rohu rastru, osa \(x\) jde ve směru zleva doprava a osa \(y\) shora dolů (obrázek 12).

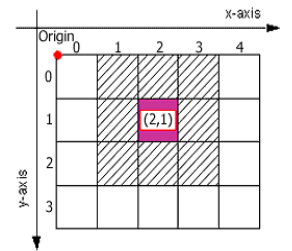
Obrázek 12: Diskrétní souřadnicový systém (zdroj: https://www.esri.com/about/newsroom/arcuser/understanding-raster-georeferencing/)

Při praktické práci s rastry v prostředí GIS však obvykle nepracujeme s lokálními diskrétními souřadnicemi, ale většinou je transformujeme do globálního kontinuálního souřadnicového systému. Poté je možné stanovit globální souřadnice jednotlivých buněk. Přitom by mělo platit, že pro celou plochu buňky jsou souřadnice stále stejné (konstantní), odpovídající buďto globálním souřadnicím některého z rohů buňky, nebo středu buňky. souřadnice se mění skokem při překročení hranice mezi dvěma buňkami.

8.1.1.2 Lokální souřadnicové systémy

Tyto souřadnicové systémy se opět dělí podle plynulosti změny souřadnic na:

kontinuální souřadnicové systémy,
diskrétní souřadnicové systémy.

Lokální kontinuální souřadnicové systémy

Lokální kontinuální souřadnicové systémy jsou založeny na kontinuálním měření polohy geoprvků, bez skokových změn souřadnic a přerušování.

Lze je podle způsobu odvozování polohy geoprvků dále dělat na:

absolutní,
relativní.

Absolutní souřadnicové systémy jsou založeny na stanovování polohy pomocí souřadnic udávajících vzdálenost podél souřadnicových os vzhledem ke společnému počátku.

Naproti tomu relativní systémy vycházejí z určování polohy geoprvků pomocí souřadnic, udávajících vzdálenost podél dvou zadaných směrů od počátku, který je ztotožněn s některým známým, pevným a snadno rozpoznatelným bodem v terénu (např. roh domu, vchod do domu apod.).

Absolutní lokální kontinuální souřadnicové systémy

Tyto souřadnicové systémy se mohou vztahovat prakticky jen k rovině. V podstatě jsou reprezentovány tzv. lokálním souřadnicovým systémem (v užším slova smyslu), kerý je definován náhodně zvoleným počátkem a dvěma směry souřadnicových os a který platí jen v omezeném areálu. Použití takovýchto systémů má své výhody i nevýhody. Základní výhodou je, že můžeme měřit prakticky kdekoliv a kdykoliv, nejsme závislí na provedení tzv. připojovacího zařízení, kterým se připojujeme ke globálnímu souřadnicovému systému (např. k S-JSTK).

Nevýhodou však je, že je obvykle jen otázkou času, kdy bude nutné navázat tento lokální systém na systém globální. A pak obvykle nezbývá, než znovu zaměřit několik bodů, tentokrát v absolutních souřadnicích a pak provést transformaci lokálního systému do globálního, popřípadě provést celé měření znovu.

Relativní lokální kontinuální souřadnicové systémy

Tyto souřadnicové systémy mohou být defivány ve vztahu k:

rovině - jde o relativní systémy udávající polohu relativně vzhledem k určitým pevně lokalizovaným objektům, jejichž poloha je známa i v absolutních souřadnicích. V podstatě jde o modifikaci předcházejícího případu s tím, že počátek lokálního souř. systému je totožný s význačným bodem na povrchu terénu (např. roh domu, vchod nebo zvláštním způsobem vyznačený bod na stěně domu) a směry a orientace os jsou dány rovněž ve vztahu k význačným směrům na povrchu terénu (např. podél a kolmo ke stěně domu). Takovéto souřadnicové systémy jsou běžně používány při lokalizaci průběhu vedení a ovládajících prvků inženýrských sítí, např. vodovodů a plynovodů (známé tabulky na fasádách domů), popřípadě i podzemních elektrických kabelů vysokého napětí. Nevýhodou těchto systémů je zpravidla neúplný popis průběhu vedení, dále malá přesnost a obtížná transformovatelnost do globálních souřadnic, vyplývající i ze skutečnosti, že prakticky pro každý lokalizovaný bod se zavádí vždy nový lokální souřadnicový systém. K nevýhodám také patří skutečnost, že různí správci různých inženýrských sítí vztahují polohu svých vedení k různým orientačím bodům a jejich mapy se pak obtížně porovnávají, lze-li porovnání vůbec provést. K nevýhodám patří i možost likvidace původního orientačního bodu (např. v důsledku demolice domu) a tím i ztráta “orientace”.
linii - dynamická segmentace - souřadnicový systém používaný pro stanovování relativní polohy geoprvků vzhledem k výchozímu bodu (“počátku”) podél zadané linie (tzv. staničení). Tento souřadnicový systém (obrázek 13) používají velice často správci dopravních sítí (silnic, železnic, vodních toků). Např. podél železnic jsou rozmístěny patníky s vyznačenou vzdáleností od počátku dané tratě. V případě železnic je použití takovéhoto souřadnicového systému asi nejméně problémové. Tratě se konec konců tak často nepřekládají. Daleko horší je ale situace v případě silniční sítě a vodních toků, a to zvláště v souvislosti s přechodem na používání GIS. V zásadě je zde možné rozlišit dva zdroje obtíží:
- problematická pravidelná aktualizace souřadnic geoprvků - při úpravách průběhu silnic i vodních toků se zpravidla neprovádí přeměření relativní polohy všech geoprvků vzhledem k počátku,
- generalizace průběhu liniových prvků v prostředí GIS - generalizace vede obecně ke zkracování linií, tj. pokud za této situace začneme zadávat polohu geoprvků (kanálů, parkovišť, uzávěrů inženýrských sítí atd.) podél obrazu silnice v GIS dle původně zaznamenaných vzdáleností, začnou se geoprvky postupně podél linie vzdalovat směrem od počátku v porovnání se skutečnou polohou.

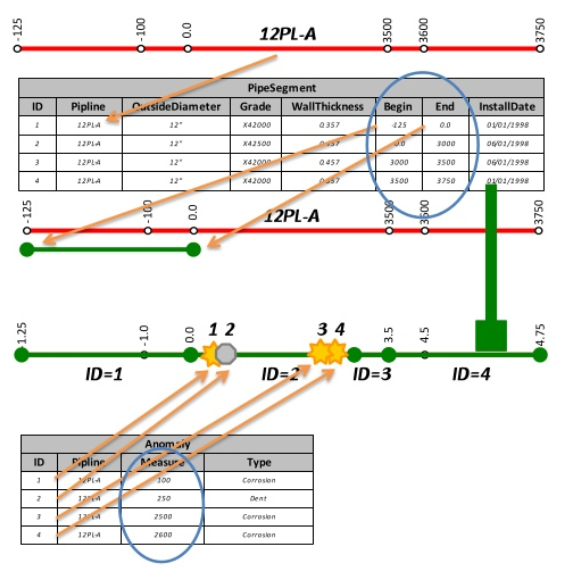
Obrázek 13: Ukázka staničení v potrubní síti

Oběma problémům se lze do značné míry vyhnout např. tak, že se podél dané linie vybuduje systém “patníků”, které signalizují přesně definované vzdálenosti od počátku linie (např. říční kilometry) a poloha geoprvků se pak stanovuje odměřením od těchto “patníků”. Vznikne tak systém lokálních souřadnicových systémů, platných vždy v oblasti mezi dvěma “patníky”. Tak se dosáhne situace, kdy se chyby ve stanovování polohy podél linie nesčítají za celou délku linie, ale jen v rámci intervalů mezi “patníky”. Je však nezbytně nutné splnit dvě podmínky:

mít všechny patníky přesně zaměřené, jejich polohu v případě úprav aktualizovat;
vlastní reprezentace linie (silnice, vodního toku) v mapě musí bezpodmínečně procházet těmito “patníky”.

Jak se to dělá v ArcGIS? Podívejte se na videa:

Lokální diskrétní souřadnicové systémy

Tyto souřadnicové systémy existují opět jen ve variantě absolutní a vztahují se k rovině. V podstatě se tyto souřadnicové systémy používají výhradně při práci s rastrovými daty. Je pro ně typické, že se souřadnice mění skokem. Poloha je definována pravidelně rozmístěnými plošnými prvky zpravidla čtvercového tvaru, odpovídajícími jednotlivými buňkám. V rámci rastru je obvykle používán lokální souřadnicový systém, jehož počátek leží zpravidla v levém horním rohu rastru, osa i jde ve směru zleva doprava a osa j shora dolů (obrázek 12). Rozměry buněk se berou jako jednotkové. Transformace do globálního souřadnicového systému není v tomto případě zavedena.

Doporučené zdroje pro další studium:

Richard Knippers: Geometric Aspects of Mapping

8.2 Restrukturalizace údajů

Existují rozdílné klasifikace činností v rámci projektu GIS, většina z nich však rozeznává etapu, ve které se manipuluje s digitálními údaji, ale cílem této manipulace není vykonat analýzy, syntézy ani vytvářet výstupy. Tato etapa bývá nazývána “předzpracováním dat”, “restrukturalizací, generalizací a transformací”. Názory na zařazení konkrétních činností do této etapy také nejsou jednotné.

Jednou ze základních forem manipulace s údaji je výběrové prostorové editování geometrických objektů při změně topologických vztahů. Mnoho vektorových GIS disponuje schopnostmi vykonávat modifikace dat na určitých omezených místech databáze. Tato operace se nazývá dílčí zpracování, resp. zpracování po částech - partial processing (např. přidání linie, která rozdělí existující plochu na dvě změní topologické vztahy).

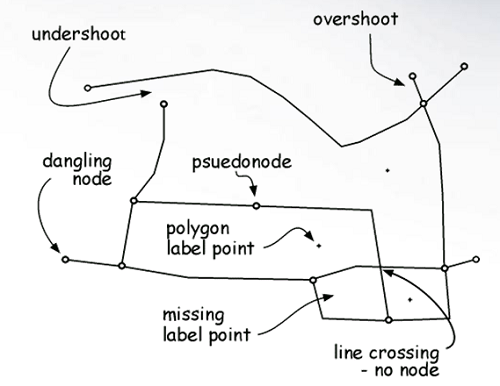
Obrázek 14: Topologické chyby vzniklé při digitalizaci (zdroj: is.humboldt.edu/OLM_2016/Lessons/GIS/08 Rasters/Images/)

Předběžné zpracování (preprocessing) dat představuje činnosti, jejichž cílem je zpracovat získaná data do požadované formy. Nebude to proces z hlediska analýzy a syntézy dat, ale spíše jejich předzpracování na tyto postupy. Celý proces zpracování (předběžného zpracování) dat lze rozdělit do dílčích kroků: restrukturalizace dat, geometrické transformace reprezentací a změna projekce mapy, konverze dat a zpracování obrazu, zobecnění.

8.2.1 Restrukturalizace dat

Restrukturalizace dat znamená zásah do všech částí geoprvků za účelem jejich přizpůsobení pro další zpracování, např. změna topologických vztahů, prostorové rozdělení vektorových a rastrových reprezentací, identifikace hran, změna rozlišení, manipulace s hodnotami atributů.

V systémech GIS je nutno organizovat velký objem prostorových údajů v databázi, proto se používají různé metody prostorového členění vektorových reprezentací. Nejčastěji je to dělení podle předdefinované čtvercové sítě nebo soustavy pravidelných hranic, které definují jednotlivé části - “mapové listy” - sheets nebo tiles. Tento proces bývá označován jako dělení na listy - tiling. Území obsažené v geografické databázi může být však také děleno na nepravidelné listy. Toto dělení je flexibilnější, vyžaduje však složitější, komplexnější zpracování. Používá se především tehdy, sledujeme-li dělení území podle národních, regionálních nebo jiných hranic.

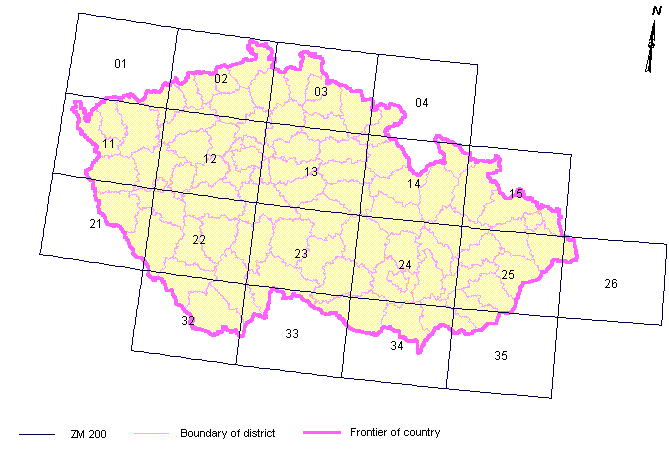
Obrázek 15: Dělení území - klady listů ZM 1:200 000 (zdroj: http://zpravodajstvi.ecn.cz/rtk/catalogue-gis/eng/polohop/arccr/klad.htm)

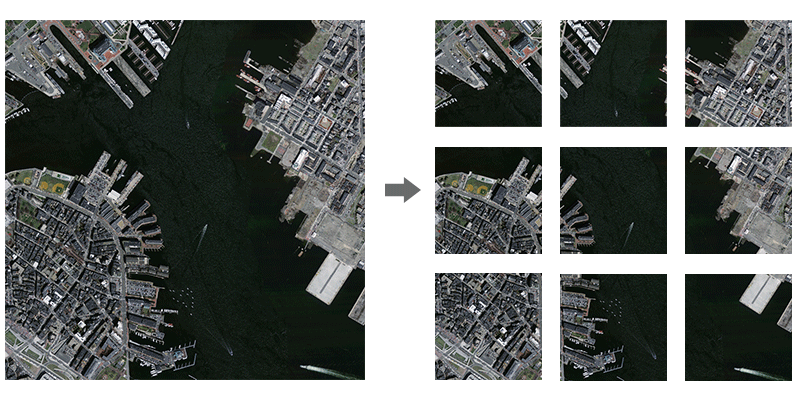
Obrázek 16: Dělení družicového snímku na dlaždice (zdroj: http://www.avenza.com/help/geographic-imager/5.0/tiling_images.htm)

Prostorové dělení databáze na části (mapové listy) vyžaduje šetrné obhospodařování okrajů jednotlivých listů. Ztotožnění okrajů - edge-matching je proces, který zabezpečuje spojení oddělených (mapových) listů do souvislé mapy a zároveň i propojení objektů zasahujících do obou spojovaných listů. Při tomto procesu je nutno přebudovat topologii objektů, které zasahují do obou spojovaných listů.

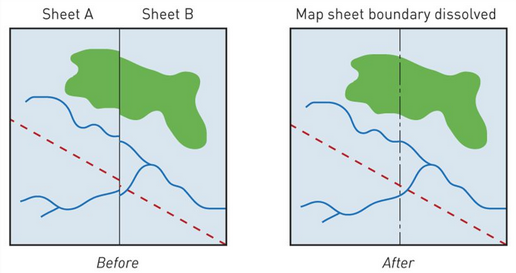
Obrázek 17: Ztotožnění okrajů - edge matching (zdroj: http://www.avenza.com/help/geographic-imager/5.0/tiling_images.htm)

8.2.2 Geometrická transformace reprezentací a změna zobrazení mapy

Geometrická transformace zahrnuje proces převodu geografických souřadnic na souřadnice pravoúhlých rovin, který se nazývá analytická transformace a převod souřadnic mezi souřadnicemi pravoúhlých rovin, tzv. Numerická transformace. Mechanismy transformace jsou založeny na přechodu definování polohy příslušného referenčního elipsoidu. GIS systémy nabízejí výkonné prostředky pro provedení analytických transformací různého druhu. Změny mezi nimi jsou vykonávány pomocí definice polohy na příslušném elipsoidu. Takovéto změny většinou označujeme jako projekce (projection).

Při práci s GIS totiž často pracujeme se třemi kartografickými zobrazeními:

zobrazením vstupních map,
interním zobrazením systému,
zobrazením mapových výstupů.

Často jsou vstupní mapové podklady vyhotovené v různých kartografických zobrazeních a měřítkách, proto je nutno transformovat je do interního jednotného souřadnicového systému. Transformace souřadnic mezi rovinnými pravoúhlými souřadnicovými systémy se nazývají numerické transformace. Nevyžadují znalost zobrazovacích rovnic kartografických transformací do původního a nového souřadnicového systému. Jsou založeny na poznání přesné polohy vybraných bodů v obou souřadnicových systémech. V praktických aplikacích jsou používány dvě metody:

lineární konformní transformace (Helmertova) - je dána vztahy:

\(x´=m\cdot x\cdot \cos \beta+m\cdot y\cdot \sin \beta+a\)

\(y´=-m\cdot x\cdot \sin \beta+m\cdot y\cdot \cos \beta+b\)

je vhodná pro transformaci mezi takovými souřadnicovými systémy, které jsou vzájemně posunuty, pootočeny a ve směrech obou souřadnicových os mají změněné měřítko ve stejném poměru. Parametry transformace určujeme pomocí referenčních bodů, jejichž souřadnice známe v obou souřadnicových systémech. Aby byl odhad parametrů transformace optimální, používá se větší množství referenčních bodů. Hodnoty koeficientů transformace se pak počítají metodou nejmenších čtverců, při které se minimalizuje suma rozdílů v poloze mezi souřadnicemi referenčních bodů v obou souřadnicových systémech.

polynomická transformace - jejím speciálním případem je afinní transformace (polynomická transformace prvního řádu), která je dána vztahy:

\(x´=a\cdot x+b\cdot y+c\)

\(y´=d\cdot x+e\cdot y+f\)

Koeficienty transformačních rovnic se počítají také metodou nejmenších čtverců. Afinní transformace je používána při transformaci souřadnicového systému digitizéru do souřadnicového systému mapy.

U rastrových reprezentací má povahu analytických i polynomických transformací proces převzorkování - resampling údajů buněk. Při převzorkování se podle transformačních rovnic vypočítá poloha středu každé buňky nové reprezentace v souřadnicovém systému vstupní reprezentace - transformuje se do ní. Po identifikaci středu buňky je možné přiřadit nebo vypočítat pro ni atributovou hodnotu z hodnot uložených v buňkách původní reprezentace. Existuje více technik k určení této atributové hodnoty:

přiřazení hodnoty nejbližšího souseda (nearest neighbour assignment) - transformované poloze středu buňky se přiřadí atributová hodnota uložená v buňce původního rastru, jejíž střed se nachází transformované nejblíže

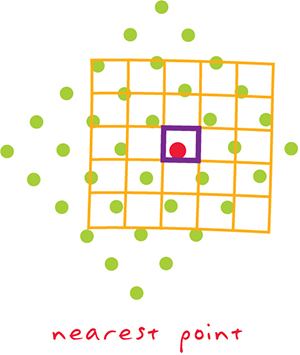
Obrázek 18: převzorkování metodou nejbližšího souseda (zdroj: https://support.esri.com/en/other-resources/gis-dictionary)

bilineární interpolace - identifikují se středy čtyř nejbližších buněk původní reprezentace vůči transformovanému středu výstupní buňky, které se přiřadí průměrná hodnota z těchto čtyř buněk vážená vzdáleností

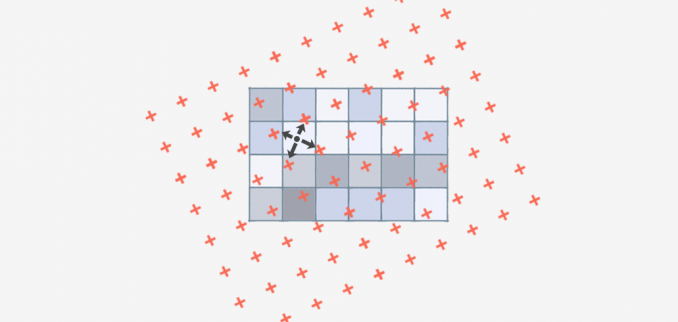
Obrázek 19: převzorkování metodou bilineární interpolace (zdroj: https://gisgeography.com/bilinear-interpolation-resampling/)

kubická konvoluce - podobná bilineární interpolaci, ale přiřazovaná hodnota se vypočítává jako vzdáleností vážený průměr ze šestnácti nejbližších hodnot vstupní reprezentace

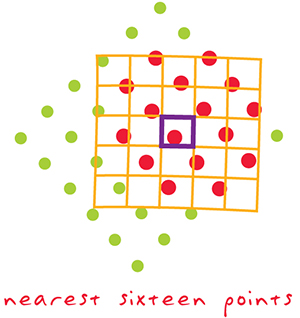
Obrázek 20: převzorkování metodou kubické konvoluce (zdroj: https://support.esri.com/en/other-resources/gis-dictionary)

8.2.3 Převod dat a zpracování obrazu

Zpracování obrazu je proces, který se používá především pro rastrové systémy a vzdálené snímání. V GIS je použití omezené; Následující seznam dokumentů proto obsahuje pouze zlomek funkcí, které tento proces zahrnuje. Mezi funkce zpracování obrazu patří: filtrování (detekce hran, vyhlazení a zaostření hranic), modifikace histogramu, změna jasu a kontrastu, klasifikace atd. Převod dat umožňuje přechod mezi formáty vektorových a rastrových dat. Během rasterizace (konverze vektoru do rastrového formátu) je vektorová vrstva překryta rastrovou mřížkou buněk pevné velikosti, ke které je přiřazen správný atribut. Problémy s touto konverzí mohou nastat, když po překrytí obsahuje jedna buňka části více objektů. Výsledná situace je pak řešena metodou centroid, metodou dominantního typu nebo metodou nejdůležitější kategorie. Vektorizace bodů je poměrně jednoduchá. Ve vektorové reprezentaci je identifikováno umístění bodu, který odpovídá středu rastrové buňky. Podobně je možné pokračovat s linkami, když se sousední buňky propojí.

8.2.4 Generalizace

Generalizace v prostředí GIS je proces, jehož cílem je zobecnit obsah prostorové databáze pro zobrazování map a komunikačních procesů a analytických procesů. Prvními požadavky na zobecnění jsou ekonomické požadavky, které zdůrazňují, že jakékoli modelování reality vyžaduje finanční prostředky a zároveň je také omezeno technickým rozvojem. Další v řadě jsou požadavky na snížení objemu dat, které kombinují zobecnění s potřebou odfiltrovat potenciální chyby vzniklé v procesu vytváření GIS. Poslední důvod zobecnění - požadavek vizualizace a vnímání dat - je založen na základních kartografických doporučeních, která (s ohledem na čitelnost mapy) naznačují míru naplnění. Nejběžnější generalizační techniky jsou: výběr - výběr prvků, eliminace - odstranění prvků, zjednodušení prvků, agregace - kombinace menších prvků do větších, prostorové zmenšení prvků, typizace - snížení hustoty prvků, přehánění - zvýraznění prvků , reklasifikace a propojení prvků, řešení konfliktů, zdokonalení - vyhlazování prvků nebo redukce vrcholů.

Při generalizování vektorových dat je kladen důraz na zjednodušení a vylepšení reprezentace liniových objektů. Při hodnocení jejich kvality se vychází především z požadavku zachování struktury informace. Čistě geometrický přístup ke generalizaci je často kritizován, proto bývají v praxi využívány kombinované postupy. Nejjednodušším postupem je ponechání jen některých lomových bodů linie podle systematického výběru. Tento postup však nezabezpečuje dokonalé zachování tvaru linie. Další možností je odstranění bodů, které se nacházejí příliš blízko k sousedům nebo mají příliš malý rozdílový úhel mezi vektory. V rámci tohoto postupu lze použít masku, obsahující postpně vždy tři body (vertexy) od počátku linie až po její koncový bod. Tyto vertexy jsou hodnoceny z hlediska vzdálenosti a rozdílového úhlu přímých úseků linie. Pokud je rozdílový úhel či vzdálenost menší než stanovený limit, je bod odstraněn.