Kapitola 1 Úvod do prostorové analýzy

Prostorová analýza (Longley et al., 1999) popisuje různé metody, které nám mohou pomoci lépe pochopit prostorové interakce mezi lidmi a prostředím. Některé komerčně dostupné systémy obsahují velmi sofistikované soubory nástrojů, avšak mnoho v současnosti řešených problémů může být vyřešeno i pomocí velmi jednoduchých prostorových filtrů využívajících vzdálenost, nejkratší cesty, dostupnost atd.

1.1 Vymezení a pojetí prostorových analýz

Obecně lze za prostorové analýzy považovat kvantitativní studium jevů, které se projevují v prostoru (Anselin 1990). Lze je tedy chápat jako specifickou skupinu kvantitativních analýz (Haining 2009b), ke které jsou potřeba data, jež se vztahují k určitému místu. I když jsou základy moderních prostorových analýz spjaty s vývojem v rámci kvantitativní geografie a regionální vědy na konci 50. let 20. století (Fischer, Getis 1997), většina prvotních prací aplikujících moderní statistické metody na prostorová data nepocházela od geografů, ale odborníků z jiných oborů (Berry, Marble 1968).

Metody prostorových analýz, které jsou dnes chápány jako relativně samostatná skupina technik, se tak rozvíjely v řadě disciplín (Horák 2002). V současnosti zaujímají prostorové analýzy významné postavení v mnoha vědeckých oborech, v nichž byla rozpoznána jejich důležitá role k uchopení a analýze velkého množství prostorových dat. Důvodem zvýšeného zájmu o prostorové analýzy v posledních letech je právě větší dostupnost kvalitních prostorových dat a dále rozšíření použití GIS a dalšího softwaru vhodného pro práci s tímto typem dat. Využití technik v rámci GIS se stalo běžné nejen v geovědách, ale také v sociálních vědách. Jak uvádí Johnston (2000), zatímco pro sociální geografii byl důležitý a přínosný vliv myšlenek z ostatních společenských věd, zejména o významu kulturních faktorů (tzv. cultural turn), pro mnoho společenských věd je v současné době charakteristický důraz na prostorové souvislosti a podmíněnosti (tzv. spatial turn). Uvedené skutečnosti se také odrážejí v koncepci tzv. „prostorově integrované“ sociální vědy (Anselin 1999, Goodchild a kol. 2000).

Pokroky v prostorové analýze se tak dějí v interdisciplinárním prostředí, ve kterém má geografie významnou, ale ne výlučnou roli. Kvantifikace a prostorové analýzy mají v geografii dlouhou historii. Po původním využívání jednodušších kvantitativních metod k charakteristice jednotlivých států a regionů docházelo pozvolna k rozvoji prostorových analýz, které dávaly do úzké souvislosti geografii a geometrii. Povaha výzkumných otázek v rámci prostorových analýz byla ovlivněna zejména lokalizačními teoriemi a individuálními pionýrskými studiemi, které lze pokládat za první příklady aplikace prostorových analýz (Berry, Marble 1968; Haining 2009a). Samotný pojem prostorové analýzy (spatial analysis) používaný hlavně v anglofonní literatuře, se v geografii rozšířil v 50. letech 20. století a je spojen s koncepcí nomoteticky zaměřené geografie jako prostorové vědy (spatial science), která reagovala na tradiční idiografické školy regionální geografie (Johnston a kol. 2000). Berry a Marble (1968) považují za cíl geografie v pojetí prostorové vědy tvorbu vhodných generalizací s prediktivními možnostmi pomocí přesného kvantitativního popisu prostorového rozmístění, prostorové struktury a prostorových vztahů.

Po období relativního úpadku aplikace prostorových analýz v geografii, které bylo spojeno s kritikou konceptu geografie jako prostorové vědy, zažívá na přelomu století geografie společně s dalšími vědeckými obory opětovný nárůst jejich důležitosti (Fotheringham, Rogerson 2009). Rozvoj digitálních datových zdrojů a informačních technologií, specificky GIS, umožnil vývoj sofistikovanějších nástrojů a metod pro analýzu prostorových dat a usnadnil jejich aplikační možnosti. Stále rostoucí technické možnosti usnadňují provádění územně velmi podrobných a početně náročných analýz, a přispívají tak alespoň k částečnému řešení mnoha metodologických problémů, které nemohly být dříve řešeny. Přesto, jak uvádí Longley (2000), mnoho podstatných metodologických limitů přetrvává. Široké rozšíření GIS mělo za následek oživení zájmu o podstatné otázky spojené s analýzou a zobrazováním prostorových dat, tedy jak o kartografii ve spojitosti s otázkou generalizace v rámci GIS vizualizace, tak zejména o kvantitativní geografii a prostorovou statistiku (Goodchild 2004b). V této souvislosti se setkáme také s konceptem tzv. geoprostorové vědy (geospatial science), která určitým způsobem navazuje na práce geografů z období kvantitativní revoluce a zdůrazňuje prostorově zaměřený výzkum (Berry a kol. 2008). Geoprostorová věda by měla propojovat přírodní a společenské vědy, neboť technicky pokročilá a vědecky relevantní analýza prostorových dat je v současné době potřebná ve většině oborů.

1.1.1 Definice prostorových analýz

Většina informací, se kterými se setkáváme a které využíváme, má prostorový charakter. Jistým způsobem je vázána k určitému místu a reprezentuje ho. Toto místo je třeba chápat v širším slova smyslu - můţe to být bod, sada bodů, linie, sada (kolekce, svazek) linií, areál. V této souvislosti pak hovoříme o geoinformacích. Formalizací informace získáváme data, obdobně formalizací geoinformace získáváme geodata (resp. prostorová data). Analogicky bychom mohli specifikovat chápání prostorových analýz jako analýzu prostorových dat, to však není správné, protože ne každá analýza prostorových dat je prostorovou analýzou - pokud např. vytvoříme histogram úplné sady prostorových dat či vypočítáme jejich základní statistické charakteristiky, nevyužili jsme prostorový aspekt těchto dat a nejde tedy o prostorovou analýzu.

Prostorové analýzy představují kolekci technik, které vznikly v různých oborech a jejichž cílem byla analýza dat s důrazem na jejich prostorové vztahy. Významné postavení mezi těmito obory zaujímá statistika, ale řada postupů byla odvozena v geografii, geostatistice, ekonometrii, epidemiologii, v územním plánování a urbanizmu. Tyto postupy jsou používány v ještě širší škále aplikací včetně např. zdravotnictví a kriminalistiky. Prostorové analýzy můžeme definovat následovně: Prostorové analýzy jsou souborem technik pro analýzu a modelování lokalizovaných objektů, kde výsledky analýz závisí na prostorovém uspořádání těchto objektů a jejich vlastností.

Objektem pro tento účel rozumíme geografické objekty a jiné objekty s prostorovou lokalizací, ať již fyzické nebo abstraktní povahy, velmi často i události a jevy.

Jak uvádí Horák (2011), vymezení pojmu prostorové analýzy nebylo dříve tak univerzálně chápáno a často se vztahovalo jen k určité oblasti aplikací či použitých postupů. Jako příklad můžeme uvést několik starších definic:

Unwin (1981): „Prostorové analýzy se zabývají uspořádáním prostorových dat na mapách (tedy bodů, linií, ploch, povrchů).“

Johnston, Gregory, Smith (1994): „Prostorové analýzy jsou kvantitativní (hlavně statistické) procedury a techniky aplikované v lokalizačních (umísťovacích) úlohách.“

Goodchild (1988): „Prostorové analýzy jsou techniky umoţňující popis uspořádání na mapách a srovnání 2 a více map s cílem identifikace jejich vztahů.“

Někteří autoři chápou termín „prostorové analýzy“ jako synonymum pojmu kvantitativní geografie, část z nich pak tento pojem uplatňuje jen pro tu část prostorových analýz, která využívá stochastické povahy jevů.

Prostorové analýzy dat jsou spjaty se studiem uspořádání prostorových dat. Zvláště se zabývají vyhledáváním nových vztahů mezi uspořádáním a atributy objektů nebo geoprvky ve studované oblasti a s modelováním těchto vztahů s cílem dosáhnout jejich lepšího porozumění a předpovídání vývoje v oblasti. Pozorované uspořádání objektů či jevů označuje Horák (2011) jako texturu (pattern), což je podle něj vhodnější než používání pojmu vzor nebo vzorek, které mají zavádějící homonyma (vzor jako něco co je vhodné následovat, vzorek (example) jako výběr jistých zástupců pro sledování celkových charakteristik).

Prostorové analýzy řeší řadu rozdílných prostorových problémů - od korekce obrazu a rozpoznání textury obrazu, přes interpolaci ovzorkovaného surovinového ložiska, průzkum prostorových a časoprostorových shluků nehod, modelování socioekonomických trendů až po studium migrace zvířat a lidí. Díky svému rozmanitému zaměření postrádají prostorové analýzy jasný systém kodifikace nebo jasný koncepční či teoretický rámec. Při úvahách o členění prostorových analýz musíme zohlednit i způsob organizace dat, protože některé funkce je možné aplikovat jen na určitém typu dat.

1.2 Historie prostorových analýz

Jak již bylo uvedeno výše, historie prostorových analýz je spojena s celou řadou oborů. Snad nejstarší kořeny mají lokalizační úlohy (hledající optimální umístění), kde již v roce 1629 formuloval Fermat úlohu nalezení bodu s minimálním součtem vzdáleností od daných 3 bodů, avšak teprve v roce 1746 ji vyřešil Torricelli. V roce 1837 úlohu zobecnil Steiner pro n-bodů a v roce 1909 umožnil Weber používat různé váhy bodů v úloze (různá atraktivita bodů) a popsal její ekonomickou interpretaci.

Jeden z prvních dokladů geografické aplikace prostorových analýz je analýza Halleye. Halley již v roce 1686 zobrazil na podkladové mapě území směry větrů a monzuny v blízkosti tropického pásma a snažil se najít jejich fyzikální příčinu.

V oblasti teorie grafů již roku 1736 řešil německý matematik Euler tzv. úlohu 7 mostů (mosty v městě Kaliningrad - viz obrázek 1). Úloha má za cíl nalézt takovou trasu, která obsahuje všechny hrany (tj. mosty) právě jednou a která začíná a končí ve stejném místě. V roce 1859 pak Hamilton řešil tzv. problém obchodního cestujícího, kdy je nutné navštívit všechny uzly v systému (vybranou sadu míst) a minimalizovat procestovanou trasu.

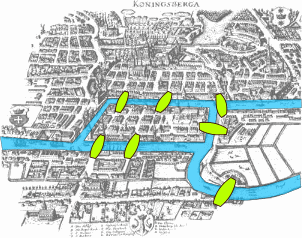
Obrázek 1: Sedm mostů v Královci (zdroj: https://cs.wikipedia.org/wiki/Sedm_mostů_města_Královce)

Řada metod byla odvozena v epidemiologii, kde první uváděnou analýzou je studie doktora Snowa z roku 1854 o způsobu přenosu cholery ve vztahu ke změnám v pozorované mortalitě v Londýně. Společně zobrazil umístění studní, výskyt nemoci a úmrtí a síť ulic a snaţil se najít vztah mezi nimi (obrázek 2). Jednou z ranných geografických analýz je i použití geografické analýzy k prokázání vztahu mezi nedostatkem slunečního záření a výskytem křivice, kterou prováděl Palm v roce 1890.

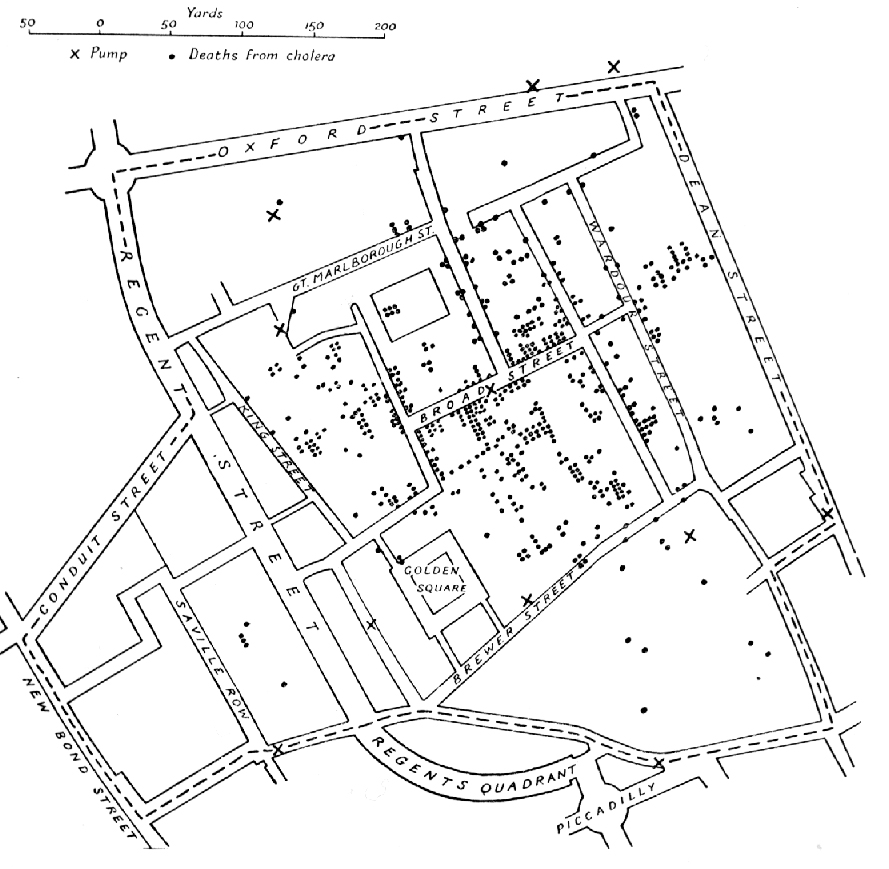
Obrázek 2: Snowova mapa cholery (zdroj: https://en.wikipedia.org/wiki/Spatial_analysis)

Mezi prostorové analýzy je moţné zařadit i využití kvadrantové metody, kdy v roce 1907 Student pomocí ní sledoval distribuci částic v kapalině a zjistil, že počet částic v kvadrantu odpovídá Poissonově distribuci.

Velmi významný metodologický přínos také představuje oblast geostatistiky, jejíž základy formuloval Matheron v letech 1962 a 1963 s aplikací poznatků z ložiskové geologie, výpočtu zásob ložisek rud, matematiky a statistiky.

Další zajímavé osobnosti prostorové analýzy najdete na stránkách Center for Spatially Integrated Social Science (CSISS Classics).

1.3 Cíle prostorových analýz

Cíle prostorových analýz se opět značně liší podle oblasti aplikací a je obtížné nalézt univerzální rozdělení. Řada autorů se pouze omezuje na výčet cílů, které reprezentují oblast zájmu pro danou aplikaci. Jako příklad může posloužit výběr cílů síťových úloh dle Laurini, Thompson (1994):

1. Najděte všechny možné trasy pro nákladní automobil v silniční síti mezi počátkem a cílem cesty (síťová analýza).
2. Najděte místo, kde je “služba” přerušena díky přerušení nebo špatné funkci sítě.
3. Najděte takovou trasu, na které se nachází nejvíce zákazníků.
4. Najděte nejbližší elektrickou rozvodnu nebo telefonní ústřednu pro nového zákazníka.
5. Umístěte nový servis v dálniční síti (typická lokalizační úloha).
6. Rozmístěte děti do nejbližších škol na základě dopravního času při cestování ulicemi (typická alokační úloha).

Při obecnějším vymezení cílů prostorových analýz můžeme rozlišit následující cíle:

1. Popis objektů resp. událostí ve sledovaném prostoru (včetně popisu jejich uspořádání - tj. textury). Zahrnuje odvození statistických charakteristik pozorované textury geoprvků (bodů, linií či areálů) a jejich srovnání; dále testování, zda je pozorovaná distribuce významně odlišná od určité hypotetické textury (což je významné pro následující interpretaci procesů); zkoušení prostorových vztahů a vazeb mezi entitami, ale i běţný popis vývoje pole např. výpočet hodnoty v neznámých místech (interpolace). Zajímá nás, proč jsou určité fenomény více seskupeny v některých místech, zda to není jen vliv náhody, jak lze porovnat texturu v různých oblastech, jak lze takový rozdíl kvantifikovat, zda dochází ke změnám v čase. Někteří autoři kritizují tento cíl, protože většina analýz končí u takového popisu a už se nezabývá vysvětlením procesů, které vedly k pozorovanému uspořádání. Navíc málokdy v přírodě odpovídá vzorek teoretickému modelu. Zde však nečekáme, že situaci bude přesně vystihovat teoretická distribuce, popis nám ale slouží k nalezení klíčových faktorů, které vedou ke vzniku určitého uspořádání.

2. Výběr určitého místa na základě splnění jisté sady podmínek (či obecněji podle jistého rozhodovacího schématu) nebo zkoumání míry splnění daných podmínek v určitém místě nebo území.

3. Interpretace procesů, které vedly k pozorovanému stavu uspořádání objektů či událostí ve sledovaném prostoru (systematický průzkum), např. interpretace vzniku pozorovaného uspořádání bodů, vysvětlení vývoje území v čase (jak střední hodnoty tak variability).

4. Optimalizace uspořádání objektů/jevů ve sledovaném prostoru např. lokalizační a alokační úlohy, volba způsobu distribuce toků (rozmístění zaměstnaných, dětí do škol, zboží), ale také např. návrh vhodného systému vzorkování.

5. Zlepšení schopnosti předpovídat a kontrolovat objekty či události ve sledovaném prostoru (využití prediktivních modelů).

6. Redukce původního množství dat do menší, úspornější a přehlednější sady dat. Provádíme např. generalizaci původních dat pro lepší popis sledovaného jevu nebo jen za účelem snadnější manipulace.

Uvedený přehled cílů prostorových analýz jistě není a ani nemůţe být úplný, protoţe s rozvojem geoinformačních technologií se nacházejí nové formy uplatnění prostorových analýz a s tím i nové cíle.

1.4 Typy používaných metod

K rozdělení metod prostorové analýzy je možné přistoupit z různých hledisek, např. z hlediska využitých postupů, způsobu zpracování, úrovně zpracování, počtu současně studovaných jevů či podle typu reprezentace prostorových objektů či jevů. Uveďme si např. rozdělení podle:

• použitých postupů (aplikovaných technik),
• způsobu zpracování dat,
• typu prostorové reprezentace.

1.4.1 Prostorové analýzy podle použitých postupů

Toto členění má zjevnou úzkou vazbu na členění disciplin, ve kterých techniky vznikaly. Podle tohoto postupu dělíme prostorové analýzy na:

• statistické prostorové analýzy (spatial statistics) - úzce spjaty s matematickou statistikou,
• mapová analýza ve smyslu mapové algebry - především překryvné operace,
• metody matematického modelování - např. tvorba a analýzy mutivariačních či regresních modelů,
• interpolační metody,
• lokalizační a alokační úlohy,
• síťové analýzy - geografické analýzy na dopravních, hydrologických či inženýrských sítích,
• ostatní analýzy okolí a spojitosti - např. techniky zpracování obrazu, používané pro získání geometrických charakteristik obrazu či textury, gravitační analýzy apod.

V případě síťové analýzy je potřebné odlišit geografickou síťovou analýzu od homonyma síťové analýzy z operačního výzkumu, uplatňované zvláště při projektovém řízení. Každá z nich má jiný význam, i když v obou případech se zpravidla řeší problém optimalizace grafů. Analýzy většinou využívají poznatky z teorie grafů, v některých případech to však není možné (nebo to není efektivní) - např. při hledání cesty terénem, který je popsán pomocí kontinuálního modelu.

Při lokalizačních úlohách řešíme problém optimálního umístění (rozmístění, lokalizace) objektů. Naproti tomu alokační úlohy řeší problém zásobování (model řízení zásob). Tyto metody se často řadí mezi síťové, protože využíváme šíření v síti. Příkladem lokalizačního problému je výběr vhodného místa pro stavbu obchodního centra, kdy vycházíme ze známé lokalizace zákazníků a známé dopravní sítě. Optimalizačním kritériem je pak maximalizace zisku plánovaného obchodního centra.

1.4.2 Prostorové analýzy podle způsobu zpracování dat

Z hlediska způsobu zpracování dat lze rozlišit metody (odpovídající 3 základním formám zpracování dat):

• vizualizační (zobrazovací),
• explorační (průzkumové),
• modelovací.

Zpracování dat můžeme chápat jako určitou posloupnost kroků, tvořících určité etapy či úrovně zpracování dat. Prvním krokem v analýze prostorových dat bývá vizualizace primárních či základním způsobem adjustovaných dat. Další etapy, tj. průzkumová či modelovací, mohou nebo nemusí být realizovány, ale pokud se provádí, tak až po této základní zobrazovací etapě. Přitom výsledky těchto etap mohou být (a zpravidla jsou) vizualizovány pomocí zobrazovacích metod.

Zobrazovací metody bychom tedy mohli ještě rozdělit podle jejich použití před či po vlastním zpracování dat na přípravné (pre-modelling) a výstupní (post-modelling) zobrazovací metody.

Vizualizační (zobrazovací) metody

Jejich cílem je zobrazení prostorových dat bez modifikace grafické složky dat. Nevyžadují statistické zpracování dat, snad pouze při vymezení hranic tříd. Často jde o vytváření map, kartogramů nebo kartodiagramů. Výsledné mapové kompozice dokumentují objekty a jevy ve sledovaném území a jsou vizuálně interpretovány. Významné je sledování rozmístění objektů, evidence výskytu shluků nebo anomálně deficitních míst, hledání příčin takového stavu, sledování trendů v prostoru a čase, vliv jednotlivých faktorů na jejich výskyt a uspořádání a jejich korelace.

Příkladem aplikace vizualizačních metod je tvorba statistických map, zvláště kartogramů a kartodiagramů.

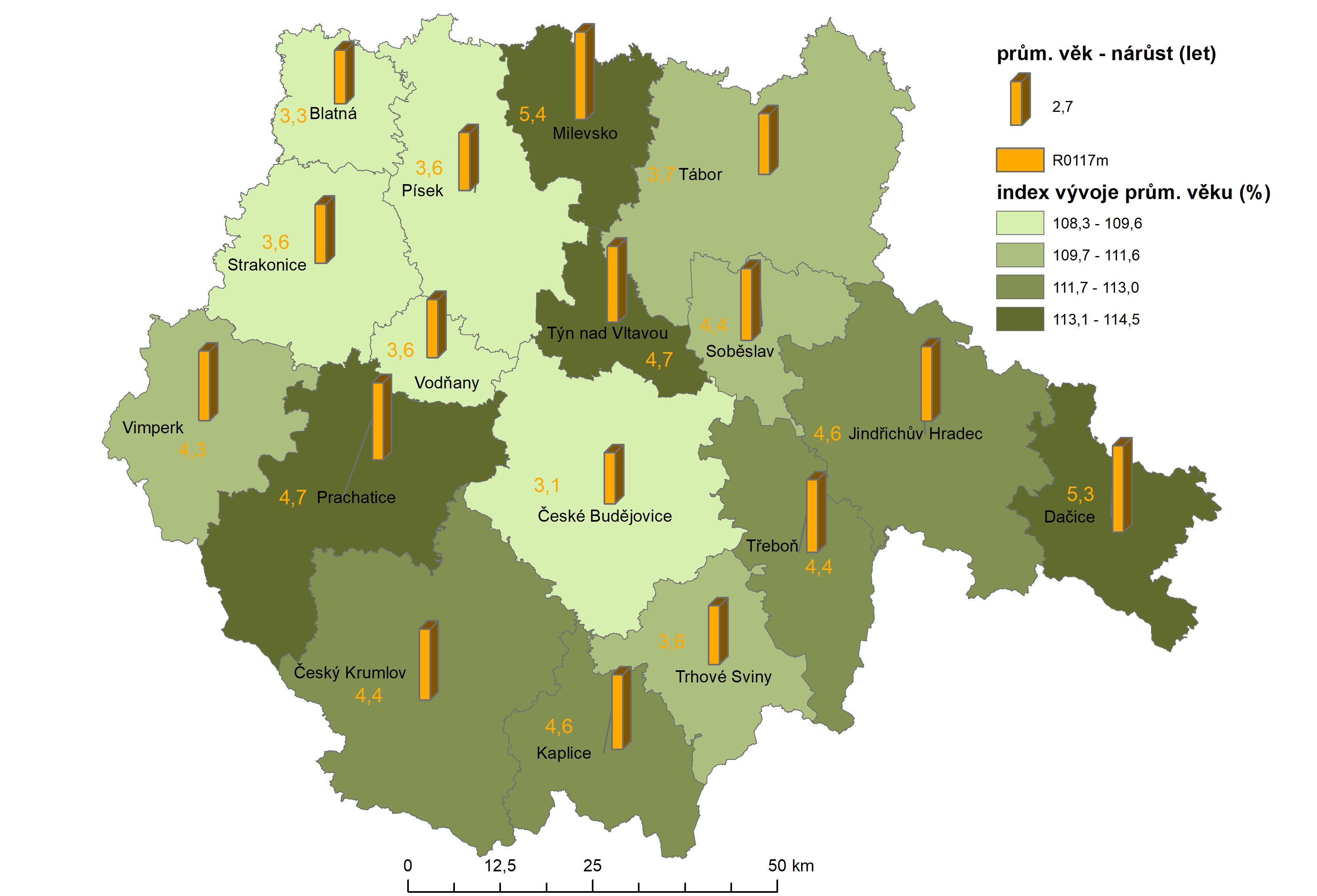
Obrázek 3: Změny průměrného věku mužů v Jihočeském kraji 2001 - 2017 (zdroj: vlastní zpracování)

Explorační (průzkumové) metody

Tyto metody nezobrazují původní data, ale používají data prostorově modifikovaná. Využívají tedy takové formy zpracování dat jako je např. vyhlazení, transformace, filtrace apod. Často provádějí sumarizaci hodnot. Zabývají se průzkumem mapové textury, vztahů a detekcí anomálií.

Zobrazovací a průzkumné metody se využívají v průzkumové analýze dat, jejichž cílem je základní průzkum vlastností dat. K hlavním rysům průzkumové analýzy dat patří identifikace vlastností dat potřebných pro účely detekce textury dat, formulování hypotéz na základě evidovaných dat a pro některé aspekty ocenění modelu (např. věrohodnosti modelu). Doporučuje se využívat jednoduché, intuitivní a statisticky robustní metody.

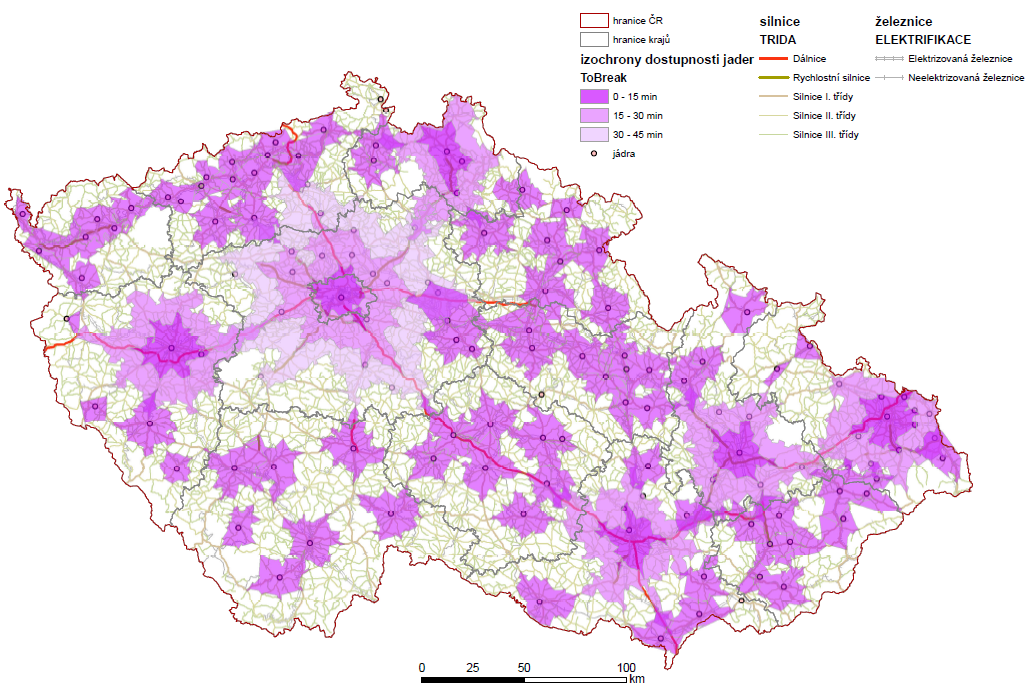
Obrázek 4: Časová dostupnost jádrových oblastí ČR 2011 (zdroj: vlastní zpracování)

Modelovací metody

Třetí skupinu metod prostorové analýzy představují modelovací metody. Jejich základem je vytvoření vhodného modelu, ověření jeho vhodnosti pro sledovaný účel (např. vysvětlení vlivu jistých faktorů) následně využití parametrů modelu pro interpretaci jevů, vztahů nebo využití modelu pro zkoumání následků jistých změn parametrů, časového vývoje apod. V oblasti modelování může k nejdůležitějším úlohám patřit prediktivní modelování, využívající často lokalizační a alokační úlohy.

1.4.3 Prostorové analýzy podle typu prostorové reprezentace

Dělení metod podle typu prostorové reprezentace odráží rozdělení prostorové reprezentace. Metody lze tedy dělit na metody vhodné pro kontinuální reprezentaci a pro diskrétní reprezentaci, kterou lze dále dělit podle typu geometrických primitiv použitých k reprezentaci (body, linie, polygony).

1.4.4 Statistické prostorové analýzy

Statistické prostorové analýzy zahrnují metody založené na stochastické (náhodné) povaze uspořádání a vztahů. Nabízejí poměrně široké spektrum aplikací. Někdy jsou přímo označovány jako prostorová statistika.

Podle počtu současně zkoumaných charakteristik můžeme používané statistické metody rozdělit na monovariační (jednorozměrné) a multivariační (analýzy vícerozměrných objektů/událostí). Používání alternativních názvů, uvedených v závorce, není příliš vhodné vzhledem k jejich snadné záměně za počet dimenzí u geometrické reprezentace objektů.

Monovariační statistické analýzy pracují současně pouze s jednou charakteristikou objektu, zatímco multivariační statistiky využívají více charakteristik současně. U multivariačních technik lze ještě specifikovat, zda studují více charakteristik současně jen vizuálně (a pak analýza a interpretace probíhá vizuálně a mentálně), nebo zda jde skutečně o multivariační metody.

Dělení podle povahy statistických technik využívá analogie z tradičního rozdělení statických technik na popisné (typicky výpočet statistických charakteristik) a indukční (na základě studia výběru usuzujeme na vlastnosti celku, provádíme testování hypotéz). Podle tohoto principu se dělí techniky statistické prostorové analýzy na:

1. popisné (deskriptivní, centrografické techniky) – především kvantitativní měření charakteristiky polohy a charakteristiky rozptýlení
2. inferenční (analýzy textury) – ty určují, zda distribuce je nebo není náhodná, popisují vztahy mezi 2 a více veličinami

Pokud hovoříme o distribuci geoprvků, máme na mysli texturu (vzor), kterou vytváří geoprvky svým rozmístěním ve sledované části prostoru.

Tři základní typy prostorové distribuce

Z hlediska statistického uspořádání geoprvků rozlišujeme 3 základní typy prostorové distribuce:

1. shluková (clustered), případně skupinová,
2. pravidelná (regular),
3. náhodná (random).

Někteří autoři ještě vymezují rovnoměrně rozmístěnou distribuci jevů, kterou lze zařadit mezi pravidelnou a náhodnou, Ivanička (1983) popisuje také aglomerizovanou a heterogenní distribuci. Většina autorů však vymezuje pouze uvedené 3 základní typy.

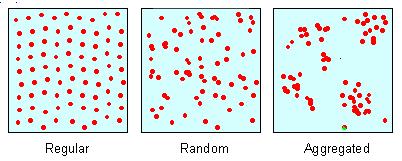
Obrázek 5: Tři základní typy prostorové distribuce - body (zdroj: https://web.ma.utexas.edu/users/davis/375/popecol/lec3/3distrib.html)

Uvedené dělení se využívá, pokud je naším cílem zjištění, zda (s jakou pravděpodobností) je prostorové rozložení geoprvků náhodné, resp. zda je statisticky průkazný jeho shlukový či pravidelný charakter. Skutečné distribuce mohou být testovány vůči těmto 3 ideálním typům, často však pouze vůči náhodné distribuci. Statisticky prokázaný výskyt shlukového či pravidelného vzorku můţe být základem pro zjišťování příčin, které vedly k pozorovanému uspořádání. Např. prokázaný shlukový výskyt případů jisté choroby může (pokud byla data správně standardizována, a to i v časové ose) podpořit hypotézu infekčního charakteru (etiologie) choroby (Horák, 2011).

Přehled základních technik pro provádění statistických prostorových analýz

Základní techniky pro provádění statistických prostorových analýz zahrnují:

1. Jednoduché deskriptivní analýzy, transformace dat a sumarizace
2. Metody nejbliţších vzdáleností (nearest neighbor) a K-funkce
3. Kvadrantové, jádrové a Bayesovské vyhlazovací metody
4. Prostorová autokorelace a kovariační struktury
5. Geostatistické a prostorové ekonometrické modelování
6. Prostorové generalizované lineární modelování
7. Multivariační techniky
8. Prostorové interakční modely

Jednoduché deskriptivní analýzy, transformace dat a sumarizace

Tyto operace často nejsou samostatně uváděny, avšak tvoří základní nástroje pro řadu dalších technik. Zařazujeme do nich jednoduché grafické a numerické metody sumarizace dat a manipulace s daty (histogramy, vyrovnání histogramu jádrovým odhadem, ogiva, rankilové grafy, rozptylogramy, “vousaté” krabičky, projekce multivariačních dat do 2D zobrazení, výpočet základních statistických ukazatelů, zjišťování korelace, transformace dat). Popis těchto technik lze najít v základních statistických učebnicích nebo publikacích popisujících průzkumovou analýzu dat.

Zařazujeme sem i základní popisnou statistiku pro prostorové objekty a jevy (např. určení středu pro shluk bodů, tvorba elipsy disperze).

Použití neprostorových statistických nástrojů k provedení prostorové analýzy lze demonstrovat 2 příkladech:

1. Výpočet Indexu stáří pro jednotlivé obce Jihočeského kraje v roce 2001. Cílem takové analýzy je zjistit a ověřit rozdíly věkové struktury v různých obcích. Pokud bychom neprovedli rozdělení celého souboru měření (resp. ukazatele stárnutí) na prostorovém základě, výsledkem by byla běžná statistická analýza Indexu stáří za celý kraj.
2. Výpočet statistiky znečištění půdy Cd a porovnání znečištění u jednotlivých potenciálních znečišťovatelů. Provede se lokalizace vzorků půd se znečištěním Cd, vytvoří se obalové zóny kolem objektů jako jsou spalovny, silnice či továrny, následně se provede výběr bodů v polygonu a vypočítají se statistické ukazatele. V tomto případu je výpočet statistických ukazatelů součástí složitější analýzy, kdy jsou vyžadovány konstrukce nových grafických objektů a řešení geometrické úlohy „výběr bodů v polygonu“ (Horák, 2011).

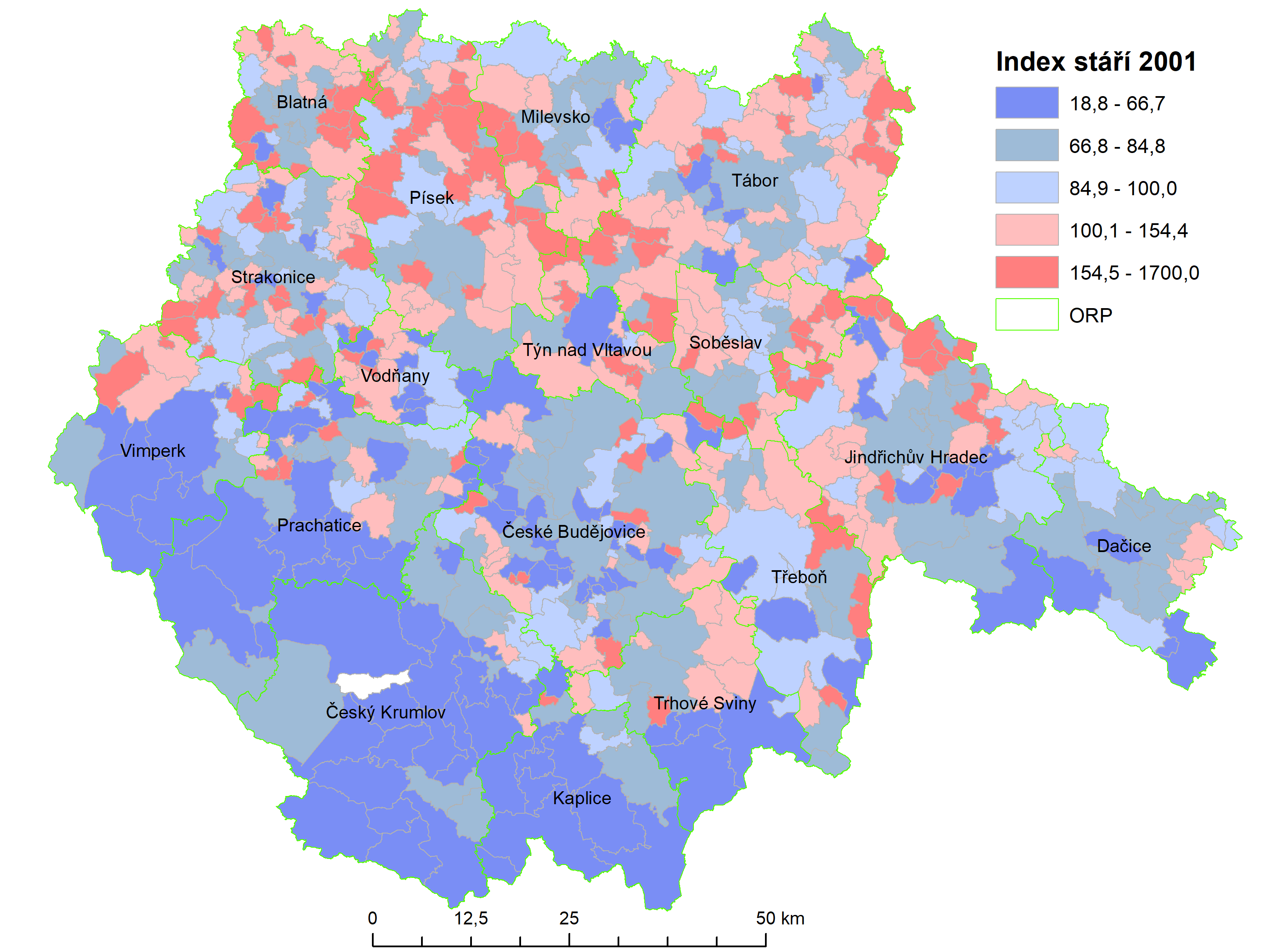
Obrázek 6: Index stáří v obcích Jihočeského kraje 2001 (zdroj: vlastní zpracování)

Metody nejbližších vzdáleností a K-funkce

Metody nejbližších vzdáleností a K-funkce jsou určeny pro posouzení umístění událostí či objektů (především bodová reprezentace) a určení typu pozorované textury (náhodná, nenáhodná).

Metody nejbližších vzdáleností jsou založeny na grafickém srovnání pozorované distribuční funkce vzdáleností mezi objekty (nebo vzdáleností mezi náhodně umístěným bodem a pozorovaným objektem) s jinými pozorovanými distribučními funkcemi nebo s očekávanou (teoretickou) distribuční funkcí získanou z modelu vytvořeného z náhodných dat.

Funkce K(h) je definována jako očekávaný počet dalších objektů do vzdálenosti h od určitého objektu. Provede se grafické nebo statistické srovnání naměřené K funkce s K funkcí odvozenou z teoretických modelů a posuzuje se typ pozorovaného vzorku.

Kvadrantové, jádrové (kernelovské) a Bayesovské vyhlazovací metody

Kvadrantové, jádrové a Bayesovské vyhlazovací metody jsou založeny na neparametrických technikách a slouží k transformaci dat z diskrétní reprezentace do kontinuální, tedy k výpočtu hustoty událostí, k vyhlazení textury apod.

V prostorovém kontextu mohou být použity např. jako průzkumné metody pro identifikaci odlišných míst (tzv. hot spots, tedy více variabilních nebo naopak více homogenních míst), pro identifikaci vhodných modelů, pro analýzu shody modelů s naměřenými daty.

Kvadrantové metody představují nejjednodušší způsob transformace dat z diskrétní reprezentace do kontinuální. V případě bodů se počítají výskyty bodů v jednotlivých buňkách překrývající měřítky. Pokročilejší metody vycházejí z myšlenky jádrového (kernelového) vyhlazování. Vyhlazená hodnota v daném bodě je vypočtena jako vážený průměr z hodnot v okolních bodech, kde váhy jsou odvozeny z distribuce pravděpodobnosti se středem v příslušném bodě.

Jádrový odhad hustoty pracuje s lokalizačními daty a pak vyjadřuje prostorově vyhlazený odhad lokální intenzity výskytu objektů/událostí. Tuto lokální vyhlazenou intenzitu je možné chápat i jako povrch rizika výskytu těchto objektů/událostí. Druhou možností je aplikace na atributová data a výpočet vyhlazeného odhadu sledovaných hodnot.

Bayesovské vyhlazovací metody jsou založeny na využití Bayesovy věty, často s aplikací Markovových řetězců.

Prostorová autokorelace a kovariační struktury

Při geostatistické analýze se povaţuje rozložení hodnot modelované veličiny (např. obsah Pb) za tzv. regionalizovanou proměnnou, která se vyjadřuje jako funkce souřadnic X,Y,Z. V každém bodě jistým způsobem vymezeného prostoru nabývá určité hodnoty. Je evidentní, že v případě přírodních objektů je hodnota v daném místě výsledkem řady procesů, z nichž některé mají výrazně náhodný charakter. Výsledkem je značná prostorová variabilita hodnot, jejich nespojitost a anizotropie.

Geostatistická analýza se snaží popsat chování této regionalizované proměnné. Jejím základním nástrojem jsou strukturální funkce.

Prostorové kovariační struktury se zjišťují v atributových datech a popisují závislost mezi rozptylem (resp. korelací) hodnot a vzdáleností měření. Uvádějí, zda a jak souvisí umístěním blízké hodnoty jedna s druhou.

Geostatistické a prostorové ekonometrické modelování

Geostatistické modelování je založeno především na provádění lokálních odhadů s využitím výsledků strukturální analýzy (aplikace interpolačních procedur).

Představují prostorové rozšíření standardních lineárních regresních modelů. Parametry jsou odhadovány pomocí funkce maximální věrohodnosti nebo zobecněnou metodou nejmenších čtverců.

Prostorové generalizované lineární modelování

Prostorové generalizované lineární modelování představuje zobecnění prostorových regresních modelů na případy, kdy modelovaná atributová data přísluší k výčtové doméně. Vycházejí z prostorového zobecnění myšlenek log-lineárního modelování kontingenčních tabulek a modelování Poissonových nebo binomických proměnných.

Multivariační techniky

Většina multivariačních technik není speciálně orientována na prostorově závislá data, ale i tak mohou být velmi užitečné jako nástroj pro redukci dat a pro identifikaci významné kombinace proměnných.

Metody se využívají např. v klasifikačních postupech při zpracování dat dálkového průzkumu Země.

Prostorové interakční modely

Prostorové interakční modely jsou založeny na modelování pozorovaného toku ze sady zdrojů do soustavy cílů. Pro soustavu zdrojů se definují požadavky, pro sadu cílů se popisuje atraktivnost. Měřítkem vzdálenosti může být i čas nebo náklady. Modely jsou běžně odvozovány ze zobecněných gravitačních modelů, zaměřených např. na minimalizaci procestovaných podmínek nebo na optimalizačních problémech - minimalizace procestované vzdálenosti, maximalizace entropie. Lze sem zařadit i lokační a alokační úlohy a tvorbu servisních území.

1.5 Vztah prostorové analýzy a GIS

Geografické informační systémy dosáhly v poslední době značného rozšíření a staly se základním nástrojem pro správu a zpracování prostorových dat i prostředníkem pro poskytování a využívání prostorových informací. Jedním z prioritních cílů vytvářených geografických informačních systémů (GIS) je podpora uživatelů při rozhodování, ke kterému využívají zprostředkování prostorových informací ve vhodné formě, často jako výsledek prostorových analýz ve smyslu společné analýzy geometrické a tématické (atributové) složky dat. Již Aronoff (1989) vyzdvihuje na GIS jako jejich nejcennější rys právě provádění prostorových analýz.

V GIS bývá k dispozici dobrá sada nástrojů pro realizaci řady metod používaných v prostorových analýzách (výběry na základě dotazování, logické operace prováděné na základě atributů geoprvků, překryvné operace, měření vzdálenosti a spojitosti, charakteristiky okolí).

Přitom je zřejmé, že některé metody nalezly velmi rychlé uplatnění v GIS (typicky metody mapové algebry), jiné se však obtížně uplatňují. Důvodem může být jejich nesnadná algoritmizace či obtížnost použití (spojená např. s požadavkem odborné erudice při provádění příslušné analýzy). Příkladem mohou být některé statistické metody, regresní modely, multivariační postupy či geostatistické modelování.

Někteří odborníci doporučují místo implementace klasických technik v geografických informačních systémech raději vývoj nových postupů, které by plně využily koncepce a metod GIS. Přebírané metody by měly být dostatečně inteligentní, aby využily více realistické reprezentace prostoru v GIS, dále by měly být vhodné pro co nejširší použití (různé aplikace), snadno algoritmizovatelné a výpočetně jednoduché.

Uvedená situace je vcelku logická a odpovídá běžnému vztahu mezi vývojem metod a aplikací specifických postupů vhodných pro určité řešení, chápaných jako rozvoj základní a aplikované vědy. Na druhé straně je nutné zcela jiné zaměření GIS chápaných jako informační systémy (IS). Připomeňme, že hlavním dogmatem informačních systémů je jednoduchost a standardizace. Proto i GIS v roli IS budou využívat především jednodušší, osvědčené a snadno aplikovatelné postupy. Ve formě flexibilního prostředí také geografické informační systémy poskytují prostor pro provádění náročných analýz a modelování. Výsledky jsou často ukládány v GIS, avšak využívány v kombinaci s jinými informačními zdroji a prezentovány pro uživatele IS.

Významný pokrok také přinesly GIS v oblasti vizualizace jak získaných dat tak i výsledků zpracování. Nástroje počítačové grafiky značně usnadnily některé nejběžnější typy výstupů, především tvorbu statistických map. Rovněž se začínají rozšiřovat i netradiční způsoby vizualizace dat.

1.6 Typy dat a jejich vztah k prostorovým analýzám

Správné využití prostorových analýz není možné bez dostatečného poznání té části světa (reality), kterou popisujeme, zkoumáme, analyzujeme nebo modelujeme. Realita je popisována na základě určitého konceptuálního modelu pomocí dat, která představují formalizovaný záznam reality (přesný význam definuje ČSN 369001). Proto je pro nás zásadní důkladné seznámení s daty, jejich správný výběr a výběr i vhodných metod pro jejich zpracování.

Prostorová data představují popis geoprvku, který zahrnuje geometrickou složku, atributovou (popisnou) složku, časovou, funkční a vztahovou složku.

1.6.1 Grafické atributy

Významná část prostorových dat vyjadřuje svou geometrickou složku popisu (tedy svou lokalizaci a prostorovou reprezentaci) pomocí grafického popisu, grafickým vyjádřením lokalizace.

Z hlediska typu vazby mezi grafickou a atributovou složkou dat (a způsobu zpracování dat) můžeme data rozdělit na:

1. lokalizační data (locational data, event data, point process). Tato data obsahují jen lokalizaci objektů či událostí. Předpokládáme, že sledujeme výskyt pouze jednoho typu objektu nebo události, o kterých kromě jejich lokalizace nic dalšího nevíme. Zajímá nás tedy, kde se to stalo (kde se vyskytly události), ne co se stalo (nezajímá nás druh či popis události). Příkladem může být lokalizace případů choroby, lokalizace dopravních nehod apod.

Pokud při zpracování využíváme údaje o rozdílných typech objektů/událostí, musíme použít multivariační techniky, resp. analýzu vícenásobných typů událostí.

Lokalizační data se vztahují k jednomu místu a nepotřebují popisné atributy. Prakticky se jedná o pouze grafická data. Vzhledem k charakteristice dat se uplatňují i postupy známé z počítačové grafiky. Kardinalita a parcialita vazby mezi grafickou a atributovou složkou je zpravidla 1:0.

2. atributová data (attribute data). Taková data obsahují hodnoty (atributy) spojené s nějakými objekty či událostmi. Lokalizace bývá vyjádřena body, buňkami pravidelného gridu nebo polygony. Jako příklad můžeme uvést půdní vzorky lokalizované bodem (protože mají z geografického hlediska zanedbatelný objem) a popsány např. výsledky geomechanických zkoušek či chemických analýz. Nebo jde o data z dálkového průzkumu Země uložená v pravidelné mřížce, která (po radiometrických a geometrických korekcích) odpovídají velikosti odrazivosti a emisivity příslušné části zemského povrchu. Poslední příklad se vztahuje k polygonům (resp. k areálům) - úmrtnost v jednotlivých okresech je reprezentována polygony.

Opět se tedy jedná o data vztažená k jednomu místu, ke kterému se váží jisté atributy. Z hlediska kardinality vazby mezi grafickou a atributovou složkou jde u monovariačních dat o vztah 1:1 (případně N:1), u multivariačních pak běžně o M:N.

Multivariační postupy je nutné použít v případech, kdy sledujeme současně více atributů u každého objektu. Jedním z nich může být i čas.

V řadě případů je možné využít konceptu regionalizované proměnné, tj. považovat data za geostatistická.

3. interakční data (interaction). Typicky jsou to kvantitativní měření spojená s liniemi nebo páry míst (často 2 body, mohou to být ale i sady polygonů). Příkladem může být tok spotřebního zboží z míst uskladnění do obchodů nebo migrace obyvatel mezi územními celky.Typicky jde o data vztažená ke 2 místům, proto bychom mohli hovořit o charakteristické vazbě mezi grafickou a atributovou složkou dat 2:1 či obecněji M:N.

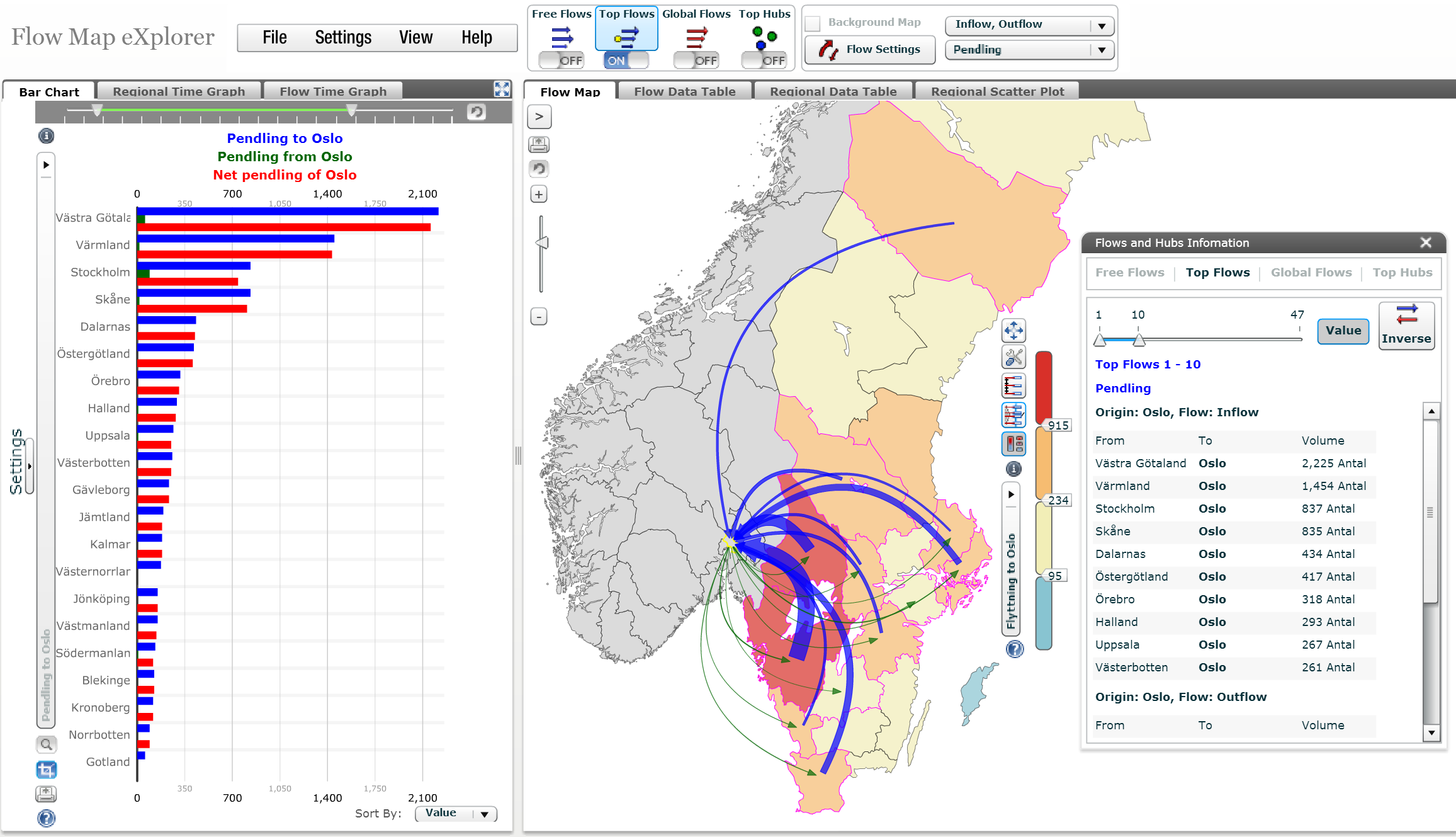
Obrázek 7: Migrační toky ve Švédsku (zdroj: https://ncva.itn.liu.se/explorer/flowmap-explorer?l=en)

1.6.2 Popisné atributy

K tématickému popisu objektů používáme atributy, přesněji popisné atributy. Atributy nám slouží k záznamu i vyjádření vlastností objektů. Postupem času (v průběhu rozvoje informatiky) se ukázalo, že je účelné přes velmi pestrou škálu informací, se kterými pracujeme, vymezit základní způsoby kódování (formalizace) dat, což má bezprostřední vliv na způsob uložení dat. Vymezení těchto základních tříd kódování vede k definici domén.

Doménu je možné charakterizovat jako potenční množinu dat, ze kterých je vybírána hodnota atributu. Základní typy domén z hlediska způsobu uložení dat v databázích jsou běžně vymezeny ve specifikaci jazyka SQL, který považujeme za základní nástroj standardizace v databázových systémech vedle nastupujícího jazyka XML.

Toto vymezení domén je založeno na způsobu uložení dat, i když určitým způsobem orientuje i dominantní způsob zpracování dat.

Jinou možností je vymezení typů domén podle způsobu zpracování dat. Vycházíme z toho, že z hlediska uložení dat pro nás může být výhodné použít např. doménu přirozených čísel, avšak interpretace těchto dat (jejich sémantika) může být velmi odlišná a může zásadně determinovat smysluplné možnosti zpracování (manipulace) dat. S číselnou doménou (zvláště racionálních čísel) je možné z matematického hlediska provádět plnou škálu matematických či statistických operací (aritmetické, goniometrické, statistické operace), při vědomí významu dat však může být množina operací omezena.

Příklad - typ pokryvu krajiny může být kódován pomocí číselného kódu. 1 pak může označovat např. lesní porost, 2 zástavbu a 3 např. vodní plochy. Předpokládejme, že jsou data zaznamenána pomocí rastrového datového modelu a že chceme provést generalizaci pokryvu, tedy jisté vyhlazení (zanedbání malých odlišných oblastí). Generalizaci můžeme provádět na základě posouzení výskytu hodnot v širší oblasti (zpravidla posuvné okno, konvoluce). Přestoţe z hlediska uložení dat jde o číselné hodnoty, nelze použít pro charakteristiku oblasti např. vážený průměr (lesní a vodní plochy ukazují v „průměru“ na zástavbu!). Jedinou možností je zde použití nejčetnější hodnoty. Tedy převažuje-li v regionu les, budeme celý region klasifikovat jako les.

Velmi jednoduché dělení nabízí rozdělení dat na kvalitativní a kvantitativní, vhodnější je ale následující přesnější vymezení čtyř tříd.

Z hlediska zpracování dat tedy rozlišujeme následující typy domén:

• poměrová (ratio) - odpovídá hodnotě na kalibrované, lineární škále ve vztahu k pevnému bodu. Takové hodnoty lze libovolně zpracovávat matematickými funkcemi. Patří sem věk, četnost, vzdálenost, cena apod. Z hlediska způsobu uložení dat jde pouze o číselnou doménu.
• intervalová (interval) - používá hodnoty s pozicí na kalibrované, lineární škále, která však nemá vztah k fixnímu bodu. Takové hodnoty lze porovnávat, ale ne např. násobit nebo poměrovat. Typickým příkladem je teplota: -5 stupňů C je o 10 stupňů méně než +5 stupňů C, ale nemá smysl vyjádřit jejich poměr (podobně i stupnice F versus C). Často charakterizují relativní pozici v prostoru, čase nebo velikost - zeměpisná šířka, nadmořská výška (problém různé srovnávací hladiny), délka, směr kompasu, čas během dne, normalizované skóre apod. Z hlediska způsobu uložení dat jde pouze o číselnou doménu.
• pořadová (ordinal) - vyjadřuje hodnotu na nekalibrované, lineární škále. Lze získat pouze kvalitativní rozdíl, ne kvantitativní. Hodnoty se tedy dají rozlišovat pořadím, ale ne velikostí. Např. 1., 2. a 3. místo na závodech nebo hodnoty „tmavě šedá“, „šedá“, „světle šedá“, „šedobílá“. Pavlík, Kühnl (1981) označují jevy popisované pomocí pořadové škály jako topologické (na rozdíl od metrických pro poměrovou škálu).
• nominální, výčtová (nominal) - hodnoty nemají vztah k lineární škále. Nelze je řadit, lze je pouze porovnat na rovnost či nerovnost. Reprezentují kvalitativní hodnoty. Typickým příkladem může být doména: {jehličnatý, smíšený, listnatý}. Nejsou kvantifikovatelné, ale pouze klasifikovatelné.

Shrneme-li, pokud použijeme k uložení dat doménu např. přirozených čísel, je aplikace matematických funkcí smysluplná pouze pro poměrová data. U intervalových dat je možné použít i rozdíl hodnot. Funkce maximum, minimum lze aplikovat i na pořadové hodnoty. Na výčtové hodnoty lze uplatnit pouze takové funkce jako testování shody, zjišťování variability, modus apod.

Někteří autoři (Pavlík, Kühnl 1981) vyčleňují z nominálních (výčtových) dat ještě binární data (ve smyslu dvouhodnotové logiky). Je zjevné, že pro takovou doménu by bylo možné uplatnit pouze testování shody a zjišťování variability už je smysluplné pouze při uplatnění prostorového charakteru úlohy (např. iterační testy náhodnosti sekvence jako je 11000101…).

Kraak, Ormelling (1996) uvádí vazbu těchto domén ke kartografickým výrazovým prostředkům (velikost, barva, tvar, textura, hodnota) a k požadovanému efektu (odlišení, uspořádání, vzdálenost, proporce). Popisují vztah k diskrétním a kontinuálním objektům a jakým způsobem se mapují. DeMers (1997) uvádí tabulku možností využití 4 základních typů domén ve vztahu k základním grafickým formám reprezentace objektů.

Přiřazení zkoumaných dat k jednomu z uvedených typů domén však představuje pouze 1. krok při jejich poznání nezbytném pro volbu správného způsobu zpracování dat (zpracování s.l. - od vstupu, uložení, analýzy, syntézy, modelování až po prezentaci).

Někteří autoři ještě vymezují různé typy indexů - density (které mají vztah k ploše), nepravé poměry, průměry a potenciály.

Podobnou situaci můžeme doložit u číselných hodnot, kdy má smysl z hlediska zpracování odlišovat veličiny absolutní a relativní:

• Absolutní veličiny zahrnují např. počet nebo hmotnost, často primární měřená či zjištěná data.

• Relativní veličiny jsou poměrná čísla (např. míra nezaměstnanosti). U relativních veličin nemá smysl provádět součet. Relativní veličiny můžeme dále rozdělit na:

  • extenzitní (ukazatele struktury, představují podíl z celku),
    

  • intenzitní (ukazatele intenzity), dále dělené na:

     * míry,
     * kvocienty, 

  • indexy, které vyjadřují časový nebo geografický vývoj.

V anglosaské literatuře se ve smyslu absolutní - relativní používá označení extenzivní - intenzivní, je třeba však upozornit, že jiní autoři používají toto označení v jiném smyslu. Extenzivní data podle nich představují měřitelné vlastnosti a intentzivní data neměřitelné vlastnosti.