Kapitola 3 Digitální modely povrchů

Znázornění terénu používali již naši předkové na starých mapách – nejprve se používala kopečková metoda, později se začalo používat různých typů šrafování a v dnešní době používáme vrstevnice doplněné o stínování. Digitální modely terénu (DMT) byly poprvé použity pro reprezentaci reálného povrchu na konci 50. let minulého stolení na Massachusetts Institute of Technology, kde sestavili tuto definici:

„DMT je jednoduše statistická reprezentace spojitého povrchu Země pomocí velkého množství bodů se známými souřadnicemi X, Y, Z v definovaném souřadnicovém prostoru“.

Od 50. let se vývoj a využití DMT posunul o značný krok kupředu a v dnešní době se s DMT setkáváme v běžném životě, aniž si to uvědomujeme – v předpovědi počasí máme simulace povodní, v ručních navigacích a telefonech zobrazíme terén, po kterém se aktuálně pohybujeme, Google Earth nám přináší celý svět ve 3D a další aplikace jsou jen otázkou zamyšlení se. V oblasti digitálního modelování výškových poměrů se lze setkat s řadou termínů a zkratek, které se často zaměňují či špatně interpretují. Terminologií se zaobírá celá řada autorů. V úvodu přinášíme přehled těchto termínů zpracovaný na základě odborné literatury.

Digitální model terénu (DMT) je model povrchu Země bez staveb, stromů a dalších objektů na jeho povrchu v digitální podobě, která dovoluje jeho zpracování prostředky informačních a komunikačních technologií (raději nepoužívejme výraz počítač, protože dnes už se nemusí striktně jednat o „počítačové zpracování“).

Zákonitě se jedná o zjednodušený model nekonečně složitého reálného povrchu, a tudíž zobrazuje tento povrch ve specifikované podrobnosti a přesnosti. V angličtině je používáno termínu Digital Terrain Model (DTM). Synonymem pro DMT je Digitální model reliéfu (DMR).

Digitální výškový model je jednou z variantou DMT V angličtině je velmi často používaný (zejména v USA) termín Digital Elevation Model (DEM), ale je téměř vždy chápán ve formě rastru (čtvercové sítě) s definovanou hustotou bodů.

Digitální model povrchu je model povrchu Země ale se všemi objekty, které na něm leží. Tento model primárně vzniká při použití automatizovaného sběru bodů pomocí obrazové korelace ve fotogrammetrii, pomocí laserového skenování nebo radarového měření v Dálkovém Průzkumu Země (DPZ). Z digitálního modelu povrchu se získává digitální model terénu teprve následným zpracováním. Ve své primární podobě se dá velmi dobře využít pro modelování a vizualizaci měst nebo krajiny včetně vegetace, vedení vysokého napětí apod. V anglickém textu se setkáte s označením Digital Surface Model (DSM).

Celou řadu dalších termínů s jejich vysvětlením a překladem do několika světových jazyků lze nalézt např. na stránkách VÚGTK, kde najdete Terminologický slovník katastru a nemovitostí.

S využitím DMT se setkáváme v celé řadě oborů a význam DMT stále roste. Jsou to např.:

vědy o Zemi – přesné informace o zemském povrchu jsou základem všech geověd. Sem můžeme zahrnout studie vlivu klimatu, geologické a hydrologické modelování, geomorfologickou analýzu, analýzu půdního krytu, geologické studie, tvorbu map různých rizik (zemětřesení, půdní sesuvy, vulkanické jevy), analýzy říčních koryt, hydrologické analýzy odtoku vody, geomorfologické simulace a klasifikace a geologické mapování.
DPZ a mapování – v DPZ a mapování jsou DMT použity společně s nástroji GIS k úpravě snímků a získání tematické informace s ohledem na geometrii senzoru a reliéfu a k získání georeferencovaných dat. DPZ a mapování můžeme řadit mezi „vědy o Zemi“.
stavebnictví – zde DMT využíváme při projektování silnic, železnic, přehrad, nádrží, pozemních úprav a těžby. Stavební inženýři používají DMT k nejrůznějším typům plánování, prezentování projektů, 3D modelování území, vizualizacím a objemovým výpočtům (přehrady, výsypky).
plánování a management zdrojů – do této skupiny patří různé obory zahrnující dálkový průzkum Země, zemědělství, pedologii, meteorologii, klimatologii, environmentální plánování a lesnictví, jejichž cílem je management přírodních zdrojů. Souhru těchto oborů si můžeme představit v následující aplikaci: definujeme oblast, která je pokryta klasifikovanými družicovými snímky upřesněnými odvozenými povrchy z DMT, známe modely půdní eroze, máme studie vhodných obilovin a modely směru větru a vývoje znečištění ovzduší. Z dostupných dat můžeme provádět analýzy výběru vhodných míst pro osev, rizika při erozi a mnoho dalšího.
vojenské aplikace – vojáci nejsou pouze jedni z největších uživatelů DMT a digitálních modelů povrchu, ale také jedni z hlavních producentů. Kvalitní DMT jsou pro tento sektor více než důležité. Ve vojenství se kombinují všechna předchozí odvětví a jejich následné využití a aplikace jsou velmi specializované a náročné. Může to být např. využití digitálního modelu povrchu pro analýzy viditelnost na bojišti, 3D zobrazení navádění zbraní a simulace letu.

Činnosti digitálního modelování terénu

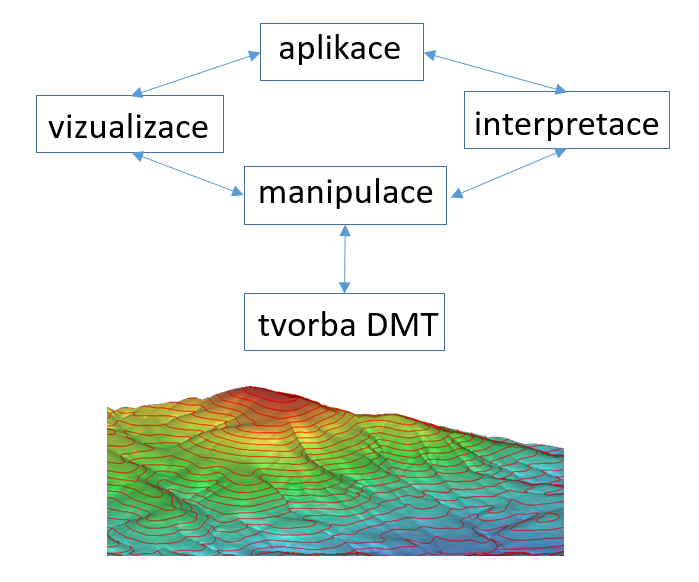
Obrázek 1: Hlavní činnosti s DMT (zdroj: upraveno podle Pacina, Brejcha, 2014)

Zjednodušeně lze konstatovat, že:

tvorba DMT zahrnuje získání výškových dat (pozemní měření, vektorizace vrstevnic, letecké snímkování, atd.) a následnou tvorbu výškového modelu,
manipulace s DMT znamená úpravy získaného DMT – odstranění chyb, vyhlazování, filtrování, konverze mezi jednotlivými datovými typy (nejčastěji TIN vs. rastr),
interpretace obsahuje analýzu DMT za účelem získaní informací pro další zpracování v GIS modelování nebo k dalším úlohám modelování terénu.
vizualizace hraje důležitou roli ve vizuálním porozumění a hodnocení. Zaměřuje se na zobrazení DMT stejně tak, jako na vizualizaci informace z DMT odvozené.
aplikace DMT je velmi široká. DMT se dostaly do bodu, kdy zajišťují klíčovou funkcionalitu pro různé aplikace. Technologický pokrok v počítačové grafice a zobrazení, prostorové teorii, prostorové databáze a mnoho dalších oborů v dnešní době umožňují zkoumat a aplikovat DMT na různé problémy.

3.1 Zdroje dat pro DMT

Data pro generování digitálních modelů terénu můžeme získat z různých zdrojů a za použití rozdílných metod. Metody můžeme rozdělit dle způsobu sběru dat do následujících kategorií:

přímé metody:
kontaktní,
bezkontaktní,
nepřímé metody.

Jak označení přímé metody napovídá, jedná se o přímo měřená (tzv. primární) data. Tato data získáme měřením v terénu za pomocí geodetických měření (nivelace, tachymetrie) a dále pomocí metody GNSS. Tato kontaktní (= měříme přímo na každém bodě) měření mohou poskytnout velmi přesné určení polohy a výšky.

Bezkontaktní metody využívají DPZ – do této skupiny patří metody fotogrammetrie (zpracování stereo-dvojic leteckých snímků), laserové skenování a radarové snímání. Tyto metody poskytují data s přesností řádově desítky centimetrů.

Nepřímé metody zpracovávají již již existující modely terénu (které mohou, ale nemusí být digitální). V případě tvorby DMT se setkáme s vektorizací/digitalizací výškopisu (vrstevnice, kóty) analogových map. Tato data pak slouží ke generování DMT. Přesnost této metody je závislá na měřítku a grafické přesnosti zdrojové mapy.

Při volbě metody vhodné pro zpracování vybrané oblasti musíme zohlednit kritéria jednotlivých metod:

velikost území,
požadovaná polohová a výšková přesnost,
požadovaná maximální hustota bodů,
čas,
cena.

Každá z metod má omezení, která ji předurčují pro některou aplikaci. Pozemním měřením lze jen těžko získat model rozsáhlého území v krátkém čase. Bezkontaktní metody mají naopak limity v přesnosti.

3.1.1 Přímé metody

Při přímém měření data vznikají již s účelem modelování terénu, a proto lze lépe stanovit požadovaná kritéria, která mají data splňovat. U přesnosti máme velmi široký výběr od „milimetrové“ přesnosti nivelace po desítky centimetrů u radarového snímání. Rovněž z hlediska rozsahu území jsou mezi metodami velké rozdíly. Obecně lze konstatovat, že kontaktní metody jsou přesnější a vhodné pro menší území oproti bezkontaktním metodám, které se výborně uplatní pro rozsáhlá území.

3.1.1.1 Nivelace

Geometrická nivelace ze středu je nejpřesnější metodou, která dovoluje určit výšky s vysokou přesností. Poněkud problematičtější může být určení polohy, které se ale většinou řeší jinou metodou (geodeticky, GPS).

Základem metody je odečítání výškového rozdílu mezi dvěma body, přičemž jeden z bodů má známu svoji nadmořskou výšku. Na oba body je postavena měřická lať se stupnicí, nivelační přístroj se umístí přibližně mezi tyto dva body a jeho záměrná přímka (optická osa dalekohledu) je pomocí libely nebo kompenzátoru urovnána do vodorovné roviny. Nadmořská výška druhého bodu se pak spočítá dle vztahu (viz obrázek 2):

\[ \triangle H_{AB}=H_{B}-H_{A}=l_{A}-l_{B},\]

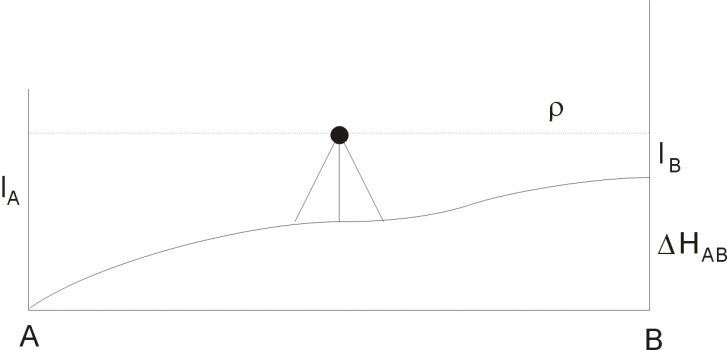
Obrázek 2: Princip nivelace (zdroj: upraveno podle Pacina, Brejcha, 2014)

Měření touto metodou je velice zdlouhavé, protože délka záměry by neměla přesáhnout 120 m a při výškově členitém území je nutné přístroj několikrát přestavovat díky omezené délce latě 3 nebo 4 metry – tím vznikají vznikají tzv. nivelační pořady. Pokud potřebujeme zaměřit terén s většími výškovými rozdíly, je nutné měřit z více stanovisek a tím se doba měření výrazně prodlužuje. Ze všech metod nivelace je pro měření bodů pro modelování nejvhodnější geometrická nivelace ze středu v kategorii přesnosti technické nivelace. Využití tato metoda nalezne při zaměřování příčných a podélných profilů vodních toků nebo pozemních komunikací nebo při variantě plošné nivelace pro určení výškových poměrů například u letišť, sportovišť. Při geometrické nivelaci ze středu umístíme nivelační přístroj na bod o známé výšce a měřická lať se postupně umisťuje na všechny vybrané body. Jejich nadmořskou výšku zjistíme opět odečtením hodnoty na měřické lati.

3.1.1.2 Tachymetrie

Pomocí tachymetrie je určována současně výška i poloha bodu v místním systému, které jsou přepočteny na souřadnice X, Y, H v definovaném souřadnicovém systému. Principem je měření délky, vodorovného a výškového (zenitového) úhlu pomocí tachymetru (teodolitu), dnes nejčastěji totální stanicí, kdy měřič signalizuje měřené body přímo v terénu výtyčkou s odrazným hranolem. Totální stanice je v podstatě elektronický tachymetr, který vzdálenosti měří pomocí laserového dálkoměru a úhly jsou odečítány pomocí elektronického systému na kódových kruzích.

Přesnost tachymetrie při použití totálních stanic je dostatečná pro většinu modelů terénu. Směrodatné odchylky/střední chyby činní zhruba 0,02–0,05 m, přičemž z jednoho stanoviska lze měřit vzdálenosti i větší než 200 m (přesnost samozřejmě se vzdáleností klesá). Vlastní metoda je velmi vhodná při potřebě přesného modelu terénu pro velká měřítka v intravilánu, u technických děl nebo pro projekční účely (např. pro pozemkové úpravy), kdy lze provést mapování do nejmenších detailů. Navíc se tato metoda často používá pro doměřování zakrytých částí území, které nebylo možné vyhodnotit například fotogrammetricky (pod vegetací).

3.1.1.3 Globální navigační satelitní systém (GNSS)

Metoda GNSS je také dobře použitelná pro měření bodů pro modelování terénu. Nejrozšířenějším systémem je dnes GPS NAVSTAR provozovaný armádou USA. Další aktivní systém je ruský GLONASS, který však nemá plně funkční konfiguraci družic a je postupně doplňován. Evropský systém GALILEO by měl dosáhnout plné operační schopnosti v roce 2019.

Všechny systémy mají stejný princip výpočtu polohy. Základem je určení vzdálenosti mezi družicí a nejčastěji právě GPS přijímačem. V systému GPS NAVSTAR kolem Země létá více jak 24 družic (8 družic ve třech drahách), které k Zemi vysílají navigační zprávu o své poloze, času vyslání zprávy a další data. Velice zjednodušeně lze říci, že k určení polohy v prostoru by postačovaly tři družice – každá ve změřené vzdálenosti družice-přijímač kolem sebe definuje kulovou plochu s poloměrem vzdálenosti k přijímači. Průnikem všech tří kulových ploch by za ideálních podmínek byly dva body, přičemž pouze jeden z nich by ležel na zemském povrchu nebo v jeho blízkosti, kdežto druhý leží kdesi ve vesmíru.

Pro modelování terénu májí dostatečnou přesnost metody diferenciální GPS/GNSS. Metoda diferenciální GPS funguje na principu oprav GPS měření v terénu. Vycházíme z myšlenky, že vliv chyb (atmosféra, hodiny, dráhy, …) je v dané oblasti o poloměru cca 40 – 50 kilometrů shodný.

DGPS (diferenciální GPS) obsahuje síť stanic, které jsou rovnoměrně rozmístěné a které provádějí měření 24 hodin denně. Každá GPS stanice (resp. její anténa) je umístěna na bodě, jehož souřadnice jsou známy a přesně určeny (např. geodeticky). Referenční stanice z rozdílu změřené polohy a známé polohy spočítá korekce, které jsou ve formě navigační zprávy odesílány GPS přijímačům pracujícím v terénu. Přenos oprav z referenčních stanic je zajištěn pomocí formátu RTCM, který je přenášen pomocí pozemního rádiového spojení, mobilními telefony, atp. Data z referenčních stanic je možné stáhnout i Internetu a data změřená v terénu následně opravit při kancelářském zpracování (postprocessing). Při tomto zpracování měřených dat můžeme získat polohovou přesnost až v milimetrech.

Mezi celosvětové DGPS sítě patří např. IGS.
Evropský systém, který zahrnuje více jak 100 referenčních stanic – EUREF.
Národní systém, používaný v rámci ČR – CZEPOS.

Další metoda, která funguje na podobném principu jako DGPS je RTK (Real Time Kinematics). Používá se při terénním měřením, kdy na bodě o známých souřadnicích umístíme GPS přijímač připojený k počítači (notebook), který počítá opravy. S druhým GPS přijímačem (obvykle anténa na výtyčce + GPS přijímač v batůžku) měříme v terénu. Korekce se mezi referenčním a terénním GPS přijímačem přenášejí např. pomocí GPRS modemu, popřípadě se aplikují při následném postprocessingu dat.

3.1.1.4 Bezpilotní letecké prostředky - drony (Unamanned Aerial Vehicle - UAV)

Novou technologií pro přímý sběr dat je metoda UAV (bezpilotní letecké prostředky, drony). Ve většině případů se pracuje s bezpilotními prostředky typu Micro-UAV (Sládek, Rusnák, 2013), které jsou osazeny běžným fotoaparátem. UAV může obecně nést téměř libovolný senzor (pouze s ohledem na váhu a napájení) – klasický fotoaparát nebo kameru, multispektrální a hyperspektrální senzory, termální kameru, snímač LIDAR nebo velmi přesnou GNSS. Výhodou systémů UAV jsou relativně nízké pořizovací a provozní náklady v porovnání s klasickým letadlem, flexibilita a možnost opakovaného snímání zájmové oblasti v různých časových obdobích (Siebert, Teizer, 2014). Na obrázku 3 je zobrazen okto-kopter SteadiDrone osazený termální kamerou Optris PI.

Obrázek 3: Okto-kopter SteadiDrone osazený termální kamerou Optris PI (zdroj: Pacina, Brejcha, 2014)

Nesený fotoaparát/senzor je připevněn na stabilizovaném držáku (tzv. gimbal), který zajišťuje neustálou vodorovnou pozici snímače při leteckých manévrech a poryvech větru. Operátor může měnit náklon a otočení kamery tak, aby se vždy snímal objekt zájmu. Získané snímky jsou dále zpracovány s pomocí software PhotoScan firmy Agisoft do podoby ortofoto snímků a DMP. S ohledem na kvalitu snímače a výšku letu je možné získat ortofoto a DMP až o rozlišení 1 pixel = 1,5 cm. Ortofoto snímky získané metodami klasické letecké fotogrammetrie od komerčních společností mají rozlišení maximálně 1 pixel = 12,5 cm (ČÚZK).

Porovnání praktického využití metody RTK GPS a UAV při terénním mapování je uvedeno např. v Siebert, Teizer (2014) – viz Tabulka 1.

Tabulka 1: Porovnání metod sběru dat

Metoda sběru	RTK GPS měření	Fotogrammetrické mapování z bezpilotního prostředku
rozloha oblasti	60,000 m\(^{2}\)	60,000 m\(^{2}\)
čas pro přípravu	30 min	40 min
čas pro sběr dat	540 min	15 min
čas pro zpracování	60 min	150 min
čas celkem	630 min	150 min
počet bodů	1800	5,500,000
hustota bodů	0,03 bodů/m\(^{2}\)	92 bodů/m\(^{2}\)
výsledky	interpretovaný model povrchu	digitální model povrchu, ortofoto

(zdroj: Siebert, Teizer, 2014)

3.1.1.5 Fotogrammetrie

Fotogrammetrie je velice rozšířená metoda pro sběr dat pro modelování terénu. Využívá dvou vhodně pořízených fotografií, pomocí nichž je schopna zpětně rekonstruovat tvar a rozměr trojrozměrných objektů. Pro fotogrammetrii se používají měřické komory umístěné na palubě letadla v závěsu, který zajišťuje minimální přenosy chvění letadla za letu a urovnává komoru do vodorovné polohy. Pro snímkování se používají objektivy o různé ohniskové vzdálenosti od širokoúhlých po normální. Konstrukce objektivů pro fotogrammetrické komory je velice precizní a jsou u nich minimalizovány veškeré optické vady. Měřítko snímku má přímý vliv na úroveň detailů, které jsou na snímku zaznamenány a tudíž má vliv na podrobnost a přesnost následného vyhodnocení. Dnes lze pořizovat jak analogové snímky na klasický fotografický film, tak přímo digitální snímky.

Pro speciální aplikace existuje i pozemní fotogrammetrie – ta využívá dvě kamery (fotoaparáty) umístěné na speciálním stativu. Tuto metodu můžeme použít např. pro výpočet kubatur v povrchových lomech.

Pro tvorbu DMT se používá letecké stereofotogrammetrie, kdy jsou snímky pořizovány z paluby letadla pomocí k tomu určené fotogrammetrické komory. Ke zpracování jsou zapotřebí vždy dva snímky (tzv. stereopár), které byly pořízeny každý z jiného místa, ale zobrazují stejné území s určitým překrytem. Snímky se pořizují v takové frekvenci, aby sousední snímky se překrývaly o nejméně 60 %. Tím je zaručeno, že celé území bude vždy zobrazeno na minimálně dvou snímcích (viz obrázek 3). Pro rozsáhlá území je provedeno snímkování v několika rovnoběžných řadách tak, aby se jednotlivé řady překrývaly alespoň o 20 %.

Obrázek 3: Princip letecké fotogrammetrie (zdroj: http://www.san-lo.com/photogrammetry.html)

Stereoskopický model je v dnešní době vytvářen pomocí počítače a snímky jsou pozorovány pomocí anaglyfických, krystalových nebo polarizačních brýlí na monitoru pracovní stanice (podobný systém, jaký se používá např. ve 3D kinech). Tyto brýle zajišťují, aby každé oko operátora vidělo jiný snímek (pravé oko pouze pravý snímek, levé oko pouze levý snímek). Při vyhodnocení snímku se využívá schopnosti lidského mozku prostorového vnímání okolí pomocí složení dvou obrazů z obou očí – využíváme stereoskopické vnímání, pomocí něhož vidíme svět kolem nás prostorově. Umělé stereoskopické vnímání, vytvořené pozorováním fotografických snímků, dovoluje operátorovi vidět vyfotografovanou krajinu plasticky a provádět na ní s pomocí virtuální měřické značky potřebná měření, například určení souřadnic bodů, určení výšky stromů nebo budov, vektorizace objektů na zemském povrchu a samozřejmě i údolnic a hřbetnic pro DMT.

Vyhodnocení snímku nemusí probíhat pouze manuálně identifikací bodu operátorem, ale můžeme plně využít digitálních fotogrammetrických stanic, které mají implementovánu korelační analýzu obrazu. Při ní se pomocí korelace identifikují stejné body na pravém i levém snímku a dochází k automatické tvorbě DMT. Efektivita práce oproti pozemnímu měření se úměrně zvětšuje s rozsahem území. Automatické korelace má ale rovněž dva základní nedostatky:

nejsou identifikovány čáry a body terénní kostry (hrany, hřbetnice, údolnice, vrcholy), které je nutné vymezit manuálně
body neleží pouze na terénu ale i na povrchu objektů (domy, stromy) a je nutné pro tvorbu digitálního modelu terénu tyto body opravit nebo eliminovat. V lesích navíc je vyhodnocení velice problematické z důvodu, že každý bod pro měření musí být viditelný na dvou sousedních snímcích. Proto se snímkování často provádí mimo vegetační období, aby koruny stromů nezakrývaly terén.

I přes uvedené nevýhody se jedná o jednu z nejrozšířenějších metod pro sběr dat pro DMT, zejména pokud je zapotřebí zmapovat rozsáhlejší území.

3.1.1.6 LIDAR - Light Detection and Ranging

Laserové skenování neboli LIDAR, se používá od 70. let minulého století, nyní se však stává stále progresivnější metodou pro mapování historických památek, průmyslových provozů, vegetace, pro tvorbu 3D modelů měst, pro sledování elektrických vedení atd.

Základním principem je dálkoměrné měření pomocí laserového svazku paprsků, přičemž je nutné znát přesnou polohu skeneru a zároveň přesný směr vyslání paprsku (viz obrázek 4). U pozemních měření se poloha a orientace skeneru určuje geodeticky a při leteckém snímkování se používá metoda GNSS kombinované s IMU (Inertial Measurement Unit) – GNSS-IMU.

Hlavní částí je pulsní nebo fázový laser, který emituje svazek laserových paprsků zpravidla v oblasti infračerveného spektra. Tento svazek paprsků je odražen zpět a senzorem zaznamenána doba mezi vysláním svazku paprsků a přijetím jeho odrazu.

Díky své šířce se laserový paprsek postupně odráží od jednotlivých vrstev objektů na zemském povrchu. Tato vlastnost se projeví nejvíce na vzrostlé vegetaci a dále pak i na hranách výškových objektů. Při mapování lesních ploch lze tedy získat jak odraz od svrchní části koruny, tak i od jednotlivých pater a rovněž i od vlastního terénu. Komerční systémy jsou dnes schopné registrovat až 5 odrazů. Z těchto několikanásobných odrazů jsou ale nejdůležitější první a poslední. První poskytuje informaci o vegetačním pokryvu nebo o vedení vysokého napětí, poslední je pak odrazem od fyzického terénu nebo od budov.

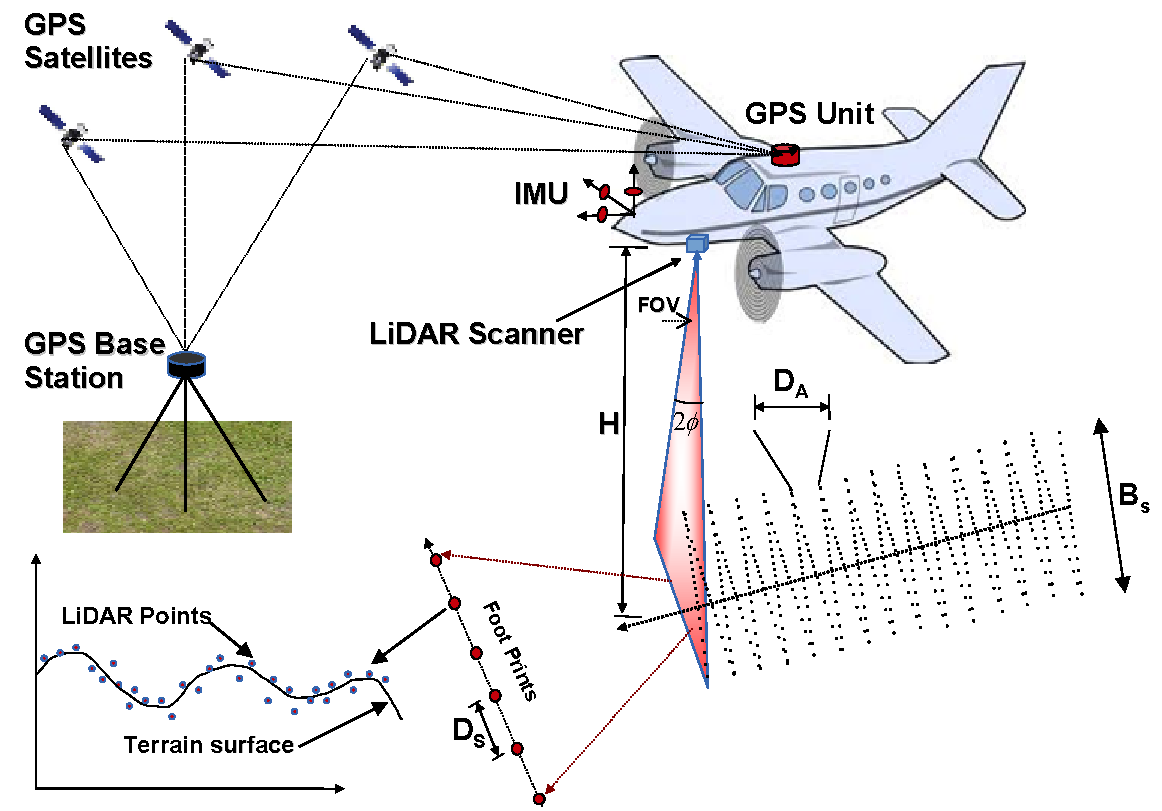
Obrázek 4: Princip LIDARu (zdroj: Dashora et el., 2013)

3.1.1.7 Radarové snímání

Radarové snímání zemského povrchu je prováděno ze satelitů již celou řadu let. Většinou jsou data používána jako obrazová data, ale protože jsou tato obrazová data výrazně ovlivněna výškovým profilem terénu, lze z nich odvozovat i výškové poměry. Radarové metody pro modelování terénu rozdělujeme na dvě základní:

radargrammetrie,
interferometrie (InSAR)

Radargrammetrie pro měření DMT užívá principu určení paralaxy, kdežto interferometrické měření je založeno na určování fázového posunu mezi dvěma měřeními.

3.1.2 Nepřímé měření

Kromě přímého měření ať už geodetickými metodami nebo metodami bezkontaktními (fotogrammetrie, DPZ) lze data pro modelování terénu odvozovat z celé řady existujících zdrojů. Nejčastěji se jedné o kartografickou digitalizaci vrstevnicového plánu zakresleného na analogové mapě, kterou lze provádět buď zcela manuálně nebo s různým stupněm automatizace až po zcela automatizované zpracování.

3.1.2.1 Vektorizace analogových map

V okamžiku, kdy nemáme digitální data k dispozici (staré mapy), tak je levným zdrojem výškových dat (můžeme použít libovolnou mapu, kterou máme k dispozici) digitalizace vrstevnic a výškových bodů z analogových (papírových) map. V dnešní době se již upouští od digitalizace map a častěji se používá vektorizace skenovaných analogových podkladů. Pro usnadnění metod vektorizace existují automatické a poloautomatické metody. Tyto nástroje jsou založeny na rozpoznávání pixelů vstupního obrazu (mapy) a následné konverze vybraných pixelů rastru do vektoru. Výsledek automatické vektorizace vyžaduje následnou kontrolu a opravu dat, protože jsou do výsledku dost často zahrnuty chyby vzniklé různými šumy a barevnou podobností pixelů zpracovávaného rastru – tudíž tato metoda nemusí být vždy rychlejší, než plně manuální vektorizace. V prostředí ArcGIS slouží pro automatickou a poloautomatickou vektorizaci rozšíření ArcScan.

Obecný postup pro vektorizaci map je následující:

Dle účelu a vymezené oblasti vybereme vhodný mapový zdroj.
Mapovou předlohou skenujeme na zvolené rozlišení (DPI).
Georeferencování mapy.
Vektorizace + přiřazení výšek.
Generování DMR.

Body 1. a 2. jsou velmi často nahrazeny již skenovanými mapami – např. staré mapy území Čech, Moravy a Slezska.

Georeferencování map

Velmi důležitým krokem při zpracování skenovaných mapových podkladů je jejich následné georeferencování. Po naskenování se mapa nachází v souřadnicovém systému obrazovky monitoru (jeden z rohů mapy má souřadnice [0,0]). Je tedy nutné mapu transformovat do cílového souřadnicového systému – v našem případě nejčastěji S-JTSK, popřípadě WGS84.

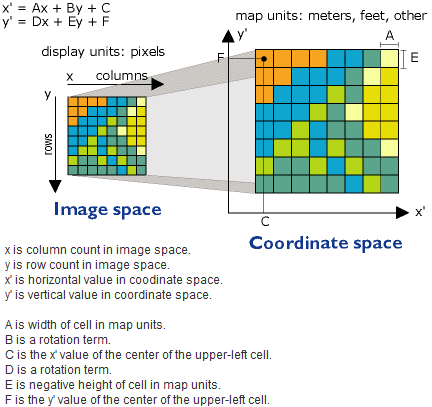
Obrázek 5: Princip georeferencování map (zdroj: https://pro.arcgis.com/en/pro-app/help/data/imagery/overview-of-georeferencing.htm)

Georeferencování je založeno na vyhledání identických bodů ve zdrojové a cílové souřadnicové soustavě:

skenovaná mapa se nalézá ve zdrojové soustavě
již georeferencovaná mapa v cílové soustavě. Můžeme použít vrstvy dostupné jako WMS a ArcGIS REST služby na http://geoportal.cenia.cz, http://ags.cuzk.cz/ – ortofotomapy, DMÚ 25, popřípadě II. vojenské mapování.

Identické body volíme tak, aby je bylo možné jednoznačně identifikovat na zdrojovém i cílovém snímku (mapě) a u kterých je malá pravděpodobnost změny v čase:

vhodné: křižovatky komunikací, kostely, rohy budov,
nevhodné: vodní toky, vodní plochy, okraje lesa.

Rozložení identických bodů na cílovém snímku by mělo být rovnoměrné. Abychom eliminovali deformaci kraje mapového listu, body by měly být rozloženy co nejblíže okraji transformovaného území. Pro georeferencování existuje několik druhů transformací pro každou z nich je dán minimální počet dvojic identických bodů nutných pro výpočet parametrů transformace. Je však dobré používat více bodů, než je požadované minimum – zpřesníme tím transformaci (snížíme polohovou chybu) a získáme informaci o přesnosti.

V ArcGIS pro georeferencování použijeme panel Georeferencing, kde je možné využít čtyři druhy transformace (obrázek 6): polynomická transformace 1., 2. a 3. řádu a spline (rubber sheeting). Jednotlivé transformace se zpřístupní až při zadání minimálního počtu identických bodů pro danou transformaci:

Polynomická transformace 1. řádu (afinní) – při této transformaci se jedná o posun, rotaci a změnu měřítka (různě ve směru osy x a y) zdrojové mapy. Minimálně potřebujeme 3 dvojice identických bodů.
Polynomická transformace 2. a 3. řádu – lépe vystihuje lokální deformace mapového listu (např. starých map) a mimo posun, otočení a změny měřítka tato transformace zohlední i pokroucení původního mapového listu.
Spline je transformace optimalizovaná pro lokální přesnost, ne však pro přesnost globální. Spline transformuje zdrojové body přesně na body v cílové soustavě a pixely mapy, které jsou od tohoto bodu vzdálené, nemusí být garantovaně transformovány přesně. Zadání více kontrolních bodů může zvýšit přesnost transformace (minimum je 10). Spline transformaci využijeme např. při georeferencování starých map, které jsou deformované a polynomická transformace 2. a 3. řádu nám neposkytuje dostatečné výsledky. Musíme zde však zmínit, že pro georeferencování starých map je vhodnější metody využívající Coonsovy pláty kombinovaná s transformací po částech. Tato problematika však přesahuje rámec tohoto učebního textu.

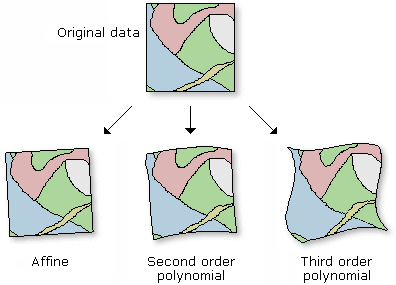
Obrázek 6: Vliv typu transformace na zdrojová data (zdroj: https://pro.arcgis.com/en/pro-app/help/data/imagery/overview-of-georeferencing.htm)

Vektorizace

Pro vektorizaci vrstevnic si založíme novou vrstvu typu polyline a pro vektorizaci výškových kót vrstvu typu point. V atributové tabulce musíme vytvořit nový sloupec pro zadávání hodnot nadmořské výšky jednotlivých vrstevnic/kót. Po dokončení vektorizace je vhodné zkontrolovat, zda máme výšku vyplněnou u všech vrstevnic. V průběhu vektorizace můžeme zpracovat také prvky terénní kostry (údolnice, hřbetnice), popřípadě některé výrazné terénní hrany (železniční násep, koryto potoka) a ty při interpolaci použít jako break lines. Pro korektní tvorbu TIN je ovšem lomovým bodům těchto hran nutno přidat nadmořskou výšku. Ukázka vektorizovaných vrstevnic je na Obr. 9.

3.1.3 Srovnání jednotlivých metod sběru dat

Výše uvedené metody mají všechny své výhody a nevýhody. Vždy je třeba sledovat celou řadu parametrů, které vstupují do rozhodování o výběru metody. Je to zejména účel, přesnost a podrobnost výsledného modelu, dále svoji úlohu hrají časová a finanční dostupnost, rozsah území, vlastní technické možnosti. V tabulce 2 jsou přehledně jednotlivé metody porovnány:

Tabulka 2: porovnání metod sběru dat pro DMT

metoda	přesnost	rychlost	cena	velikost území
nivelace	0,001 - 0,01 m	*	€€€€€€€	o
tachymetrie	0,02 - 0,05 m	**	€€€€€	o
GPS	0,02 - 0,05 m	***	€€€€	o
UAV	0,5 - 0,01 m	******	€	oo
fotogrammetrie	0,2 - 0,5 m	******	€	O
DPZ	1 - 10 m	*********	€	OO
InSAR	5 m, změny 1 cm	*********	€	OO
radarové snímání	20 - 70 m	*********	€	OO
LIDAR	0,1 - 0,2 m	*****	€€€	O
manuální vektorizace map	dle měřítka mapy	**	€€€	libovolně
automatická vektorizace	dle měřítka mapy	****	€	libovolně

(zdroj: Pacina, Brejcha, 2014)

3.2 Zdroje výškových dat pro území ČR

V našich podmínkách se nejčastěji setkáváme s daty ve formě vrstevnic, popřípadě výškových bodů (kót). Datové zdroje, které kompletně pokrývají území ČR jsou např. data poskytovaná Českým úřadem zeměměřickým a katastrálním (ČÚZK) – ZABAGED® (Základní báze geografických dat), nebo také Vojenským geografickým a hydrometeorologickým úřadem v Dobrušce – DMÚ 25. Zdarma dostupný je však i DMT ČR v rastrové podobě z mise raketoplánu Endeavour. Obecně můžeme říci, že v ČR je k dispozici celá řada map, které obsahují výškopis (např. turistické mapy). Ten je nicméně přebírán nejčastěji právě z dvou prvně jmenovaných zdrojů.

3.2.0.1 ZABAGED®

ZABAGED® je digitální geografický model území České republiky, který svou přesností a podrobností zobrazení geografické reality odpovídá přesnosti a podrobnosti Základní mapy České republiky v měřítku 1:10 000 (ZM 10). Obsah ZABAGED® tvoří 106 typů geografických objektů zobrazených v databázi vektorovým polohopisem a příslušnými popisnými a kvalitativními atributy.

ZABAGED® obsahuje informace o sídlech, komunikacích, rozvodných sítích a produktovodech, vodstvu, územních jednotkách a chráněných územích, vegetaci a povrchu a prvcích terénního reliéfu. Součástí ZABAGED® jsou i vybrané údaje o geodetických, výškových a tíhových bodech na území České republiky a výškopis reprezentovaný prostorovým 3D souborem vrstevnic.

Výškopisná data Zeměměřického úřadu poskytují informace o výškových poměrech terénního reliéfu, respektive povrchu (včetně staveb a rostlinného pokryvu) České republiky. Zeměměřický úřad v současné době spravuje a poskytuje několik výškopisných datových sad rozdílné úrovně podrobnosti a přesnosti výškopisu:

ZABAGED® - výškopis 3D vrstevnice tvoří 3 typy objektů vrstevnic se základním intervalem 5, 2 nebo 1 m v závislosti na charakteru terénu. Datová sada může být doplněna vybranými terénními hranami a body poskytovanými uživatelům v rámci produktu zdarma. Objekty jsou reprezentovány trojrozměrnou vektorovou prostorovou složkou. Přesnost výšky vrstevnic je závislá na sklonu a členitosti terénu a dosahuje 0,7-1,5 m v odkrytém terénu, 1-2 m v sídlech a 2-5 m v zalesněném terénu.
ZABAGED® - výškopis grid 10 x 10 m je digitální model reliéfu v podobě pravidelné mříže (10 x 10 m) trojrozměrně vedených (3D) bodů, který je odvozený z vrstevnic a terénních hran ZABAGED®. Přesnost výšky jednotlivých výškopisných bodů je obdobná jako u zdrojových vrstevnic, tedy 0,7-1,5 m v odkrytém terénu, 1-2 m v sídlech a 2-5 m v zalesněném terénu.
Digitální model reliéfu České republiky 4. generace (DMR 4G) představuje zobrazení přirozeného nebo lidskou činností upraveného zemského povrchu v digitálním tvaru ve formě výšek diskrétních bodů v pravidelné síti (5 x 5 m) bodů s úplnou střední chybou výšky 0,3 m v odkrytém terénu a 1 m v zalesněném terénu.
Digitální model reliéfu České republiky 5. generace (DMR 5G) představuje zobrazení přirozeného nebo lidskou činností upraveného zemského povrchu v digitálním tvaru ve formě výšek diskrétních bodů v nepravidelné trojúhelníkové síti (TIN) bodů s úplnou střední chybou výšky 0,18 m v odkrytém terénu a 0,3 m v zalesněném terénu.
Digitální model povrchu České republiky 1. generace (DMP 1G) představuje zobrazení území včetně staveb a rostlinného pokryvu ve formě nepravidelné sítě výškových bodů (TIN) s úplnou střední chybou výšky 0,4 m pro přesně vymezené objekty (budovy) a 0,7 m pro objekty přesně neohraničené (lesy a další prvky rostlinného pokryvu).
Datová sada INSPIRE – Nadmořská výška (EL) představuje Digitální model reliéfu 4. generace (DMR 4G) ve formě standardizované dle příslušné směrnice INSPIRE.

Data ZABAGED® - výškopis 3D vrstevnice jsou zpřístupněna prostřednictvím WMS prohlížecí služby ZABAGED®. Data DMR 4G, DMR 5G a DMP 1G jsou zpřístupněna prostřednictvím WMS (ve formě stínovaného reliéfu) a ve formě ArcGIS IMAGE služeb, které lze využít kromě prohlížení i pro základní analýzy výškopisných dat. Služby je možno volně využívat ve vlastních aplikacích (klientech). Na Geoportále ČÚZK lze k prohlížení WMS služeb využít aplikaci Geoprohlížeč. Možnosti využítí IMAGE služeb jsou zde ukázány v aplikaci Analýzy výškopisu.

3.2.0.2 DMÚ 25

Druhým významným zdrojem kvalitních topografických dat je vojenské mapové dílo. Správcem digitálních produktů odvozených z vojenských topografických map je Vojenský geografický a hydrometeorologický úřad (VGHMÚř) se sídlem v Dobrušce. Autorská práva k tomuto dílu spravuje Generální štáb Armády České republiky. I zde najdeme jak rastrové mapy, tak vektorové databáze, a to jako součást budovaného vojenského topografického informačního systému (VTIS). Dílem srovnatelným se ZABAGED je digitální model území DMÚ 25. Jedná se o vektorovou databázi topografických informací o území, která svou přesností a obsahovou náplní koresponduje s vojenskými topografickými mapami měřítka 1:25 000 označovanými TM25. Databáze obsahuje topografické objetky rozdělené do 7 tématických vrstev – vodstvo, sídla, komunikace, vedení sítí, hranice a ohrady, rostlinný a půdní kryt a terénní reliéf. Databáze je bezešvým digitálním modelem celého území České republiky s mírným přesahem přes státní hranici. Na rozdíl od databáze ZABAGED nekončí na státní hranici, ale zobrazuje ještě několik kilometrů široké pásmo sousedních států.

DMÚ 25 je k dispozici jako IMS a WMS2 služba na adrese Geoportálu CENIA.

3.2.0.3 SRTM data

Jedná se o data, která vznikla při misi raketoplánu Endeavour, při které byl pořízen model reliéfu celého světa. V rámci mezinárodního projektu The Shuttle Radar Topography Mission (SRTM) zaštiťovaném National Geospatial-Intelligence Agency (NGA) a The National Aeronautics and Space Administration (NASA) bylo za účelem přesného výškového zmapování povrchu Země v roce 2000 nasnímáno 80 % povrchu souše metodou radarové interferometrie (Burdea, Coiffet, 2003).

Dle Burdea a Coiffet (2003) maximální přesnost digitálního modelu terénu 15 metrů v poloze a 12 metrů ve výšce. Data jsou k dispozici v rastrové podobě s prostorovým rozlišením 1 úhlová vteřina (cca 30 metrů na rovníku) pro území USA a 3 úhlové vteřiny (cca 90 metrů na rovníku) pro ostatní svět, což pro zeměpisnou šířku střední Evropy představuje přibližně 90 × 60 metrů. Data pro ČR je možné zdarma získat na adrese firmy GISAT.

3.3 Tvorba a druhy DMT

K reprezentaci reálného terénu můžeme využít mnoho přístupů (viz obrázek 7). Vstupní data jako např. vrstevnice a výškové body tvoří tzv. nekompletní reprezentaci povrchu. Vrstevnice mají určitý interval (např., DMÚ 25 – 5 m, interval vrstevnic ZABAGED® se mění v závislosti na výškové členitosti mapového listu od 1 m po 5 m), výškové body určitou hustotu v závislosti na způsobu sběru dat (výběrové body terénní kostry získané GPS vs. husté body z LIDAR snímkování). Abychom dosáhli kontinuální reprezentaci povrchu (a dokázali „vyplnit mezery“ mezi daty), musíme provést interpolaci vstupních dat. V závislosti na požadovaném výstupu volíme mezi různými typy interpolací. V praxi se budeme nejčastěji setkáváme s reprezentací povrchu pomocí rastru a pomocí Triangulated Irregular Network (TIN – nepravidelná trojúhelníková síť).

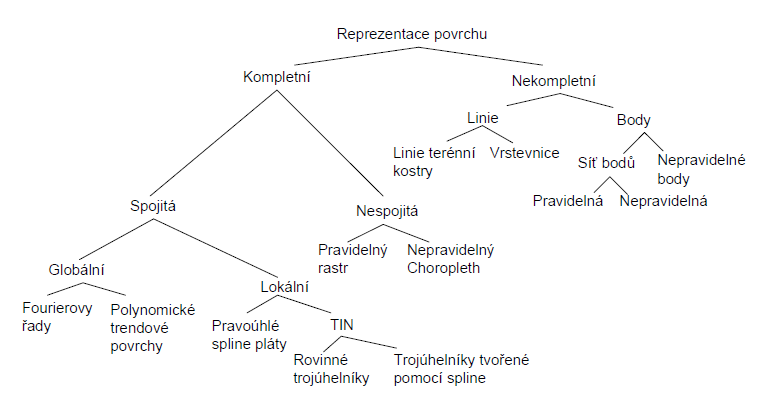
Obrázek 7: Reprezentace povrchu (zdroj: Pacina, Brejcha 2014)

Pro tvorbu DMT se používají výšková data, které neúplně pokrývají zpracovávanou oblast (např. body a vrstevnice) – viz obrázek 7 (nekompletní reprezentace povrchu). Pro „doplnění“ oblasti na kompletní reprezentaci povrchu se využívá interpolačních metod. Interpolační algoritmy se snaží na základě svého matematického základu a zadaných vstupních parametrů (které interpolaci ovlivňují) predikovat chování reálného terénu. Zde je nutné si uvědomit, že interpolační algoritmy si chování terénu mezi vstupními body „vymýšlí“. Kvalita výstupního DMT se tedy odvíjí nejen od kvality vstupních dat (přesnost, hustota), ale také od vhodně zvolené interpolační metody včetně řídících parametrů. Po dokončení tvorby DMT je tedy vhodné provést ověření kvality/přesnosti výsledku.

Výsledkem je řada druhů DMT, které se navzájem liší použitým algoritmem vytváření modelu, datovou strukturou uložení výsledku, vhodností pro vizualizaci, či naopak analýzu. Pro zájemce o podrobnější studium lze odkázat na literaturu (Bayer, 2016).

3.3.1 Tvorba DMT

Podkladem pro digitální model jsou body se třemi souřadnicemi (a s atributy). DMT je však plocha konstruovaná nad vstupní množinou bodů.

Požadavky na tuto aproximační plochu:

prochází všemi body,
co nejvěrněji zobrazuje terén (co nejvíce se k němu přimyká),
bezdůvodně neosciluje,
umožní znázornit singularity (tj. nespojitá místa v terénu),
Výpočet parametrů aproximační plochy v reálném čase (on-line operace s DMT),
numerická stabilita výpočtu,
malá citlivost na vstupní data.

Aproximační plocha prochází zadanými body, mimo ně je dopočítávána tak, aby se co nejvíce blížila skutečnému terénu. Terén rozsáhlejší oblasti nelze popsat jednou matematickou plochou – musí to pak být plocha velmi vysokého stupně, která samovolně osciluje. Používá se proto technika, kdy se terén se rozdělí na jednoduché a snadno popsatelné oblasti.

3.3.2 Druhy DMT podle typu ploch

Podle použitého typu ploch rozlišujeme:

Polyedrický model terénu (nepravidelná trojúhelníková síť, jednotlivě roviny).
Rastrový model terénu (čtvercová síť, jednotlivě roviny).
Plátový model terénu (složitější, většinou nadstavba nad předchozí dva druhy – aproximace vyšším řádem).

Při tvorbě DMT je využívána technika plátování, která spočívá v rozdělení aproximační plochy na větší množství malých ploch nižších stupňů - pláty. Pláty nejčastěji stupně tři kubické pláty (kubické polynomy), které již věrně aproximují terén, jejich výpočet je poměrně snadný. Digitální model je tvořen velkým množstvím plošek (řádově stovky tisíc, milióny), mezi nimi ostré nebo hladké přechody. Tímto způsobem lze popsat jakýkoliv terén. Poprvé použito v 70. letech při konstrukci letadel (Airbus = Bezierovy pláty, Boeing = Coonsovy pláty).

3.3.2.1 Polyedrický model terénu (TIN)

V tomto modelu představují jednotlivé plošky jsou nepravidelné trojúhelníky, společná je nejvýše hrana. Síť trojúhelníků vytvořena za použití triangulačních algoritmů. Proložením rovin vrcholy jednotlivých trojúhelníků vznikne nepravidelný mnohostěn (tzv. polyedr), který se přimyká k terénu. V trojúhelnících pak lineární interpolace. Tvar území může být konvexní i nekonvexní, s otvory (místa bez vrstevnic) či bez. Lze zadat povinné spojnice (hřbetnice, údolnice, spádnice), které zlepšují jeho aproximační vlastnosti. Pro konstrukci používána Constrained Delaunay Triangulation.

Podle Krevelda (1997) je triangulace vstupních bodů do podoby TIN velmi všestranným způsobem reprezentace reálného terénu. Výsledné trojúhelníkové plošky TIN jsou většinou považovány za rovinné a díky tomu poskytují plně definovaný a spojitý model terénu. Hlavní výhodou triangulovaných povrchů je adaptabilita s ohledem na vstupní data:

oblasti s velkou variabilitou terénu jsou pokryté hustou sítí bodů → vzniká velké množství malých trojúhelníků,
ploché oblasti (nebo s konstantním sklonem) obsahují méně bodů = vznikají velké trojúhelníky.

Narozdíl od TIN jsou reprezentace povrchu pomocí pravidelného rastru náchylné k nadhodnocení nebo podhodnocení (z angl. overestimation, underestimation) při pokrývání oblastí s výrazně odlišnou strukturou a členitostí. Pravidelný rastr má pevně stanovenou velikost buňky a při změně členitosti terénu pak rovinnou oblast pokrýváme rastrem s malou velikostí buňky nebo naopak členitý terén rastrem s velkou velikostí buňky (např. kontrast Mostecká pánev a Krušné hory).

V datovém modelu TIN jsou body uloženy společně s jejich nadmořskou výškou. Každý trojúhelník pak obsahuje informaci, ze kterých hran se skládá a každá hrana obsahuje informaci, které body ji definují. TIN je po částech lineární model, který může být v prostoru vizualizován jako jednoduše propojená síť trojúhelníků, která je spojitá, ale není v celé oblasti diferencovatelná.

Pro tvorbu TIN se používá metoda zvaná triangulace = tvorba trojúhelníkové sítě z množiny vstupních bodů. Jednou z podmínek je, aby triangulace produkovala co možná nejvíce rovnostranné trojúhelníky a aby výsledek triangulace byl nezávislý na orientaci dat a volbě počátečního bodu. Tyto podmínky splňuje např. Delaunayho triangulace.

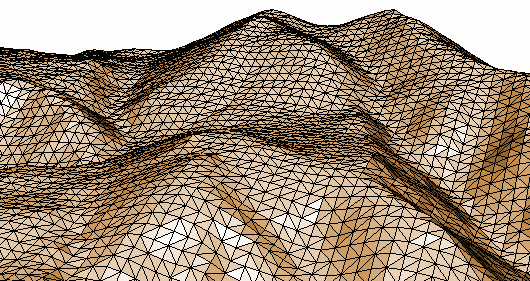
Obrázek 8: Delaunay povrch (zdroj: https://www.geom.at/terrain-triangulation/)

Princip algoritmu Delaunyho triangulace je velmi jednoduchý – třemi body je proložena kružnice. Zkoumá se, zda uvnitř kružnice proložené třemi body leží další bod – pokud ano, zvolí se jiné tři body. Pokud ne – z testovaných bodů se vytvoří trojúhelník (viz předcházející kapitola).

Při triangulaci může dojít ke vzniku tzv. rovinných (vodorovných) trojúhelníků. Ty se vytvářejí ve chvíli, kdy algoritmus vybere pro tvorbu trojúhelníku pouze body o stejné nadmořské výšce. Dochází k tomu zejména u vrcholů kopců a v okolí hřbetnic a údolnic, kdy dochází k tvorbě umělých „schodů“ (obrázky 9 a 10). Tyto trojúhelníky mají sklon 0° a nemají definovanou orientaci vůči světovým stranám – to může způsobovat problémy při následných analýzách a modelování. Tato chyba se dá odstranit dodáním výškových bodů nebo linií terénní kostry.

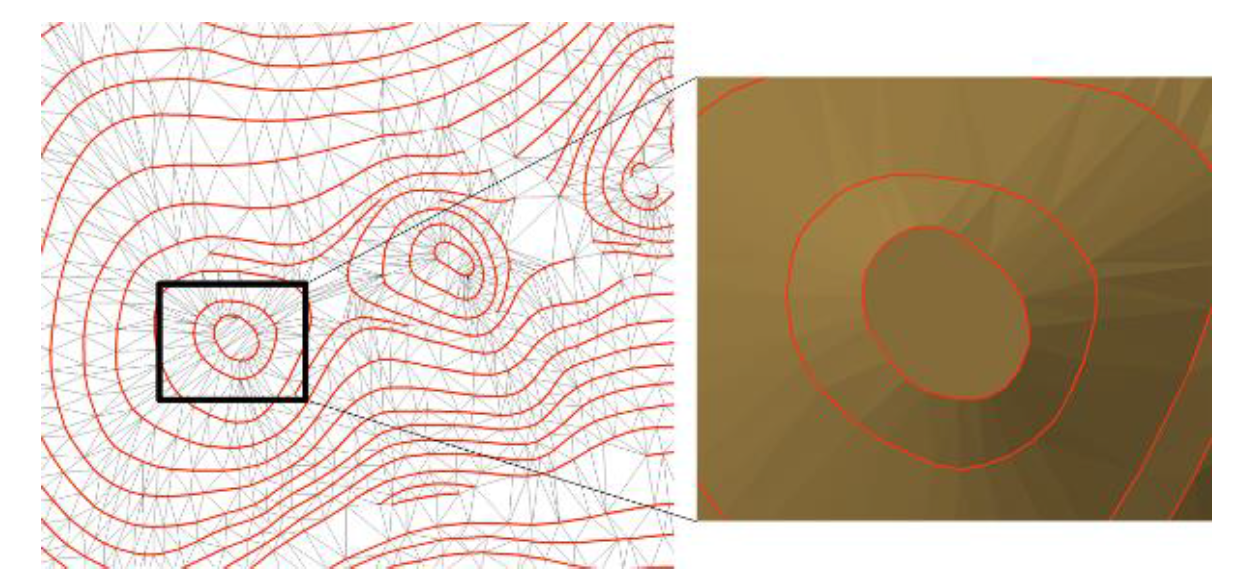
Obrázek 9: Ploché trojúhelníky (zdroj: Pacina, Brejcha, 2014)

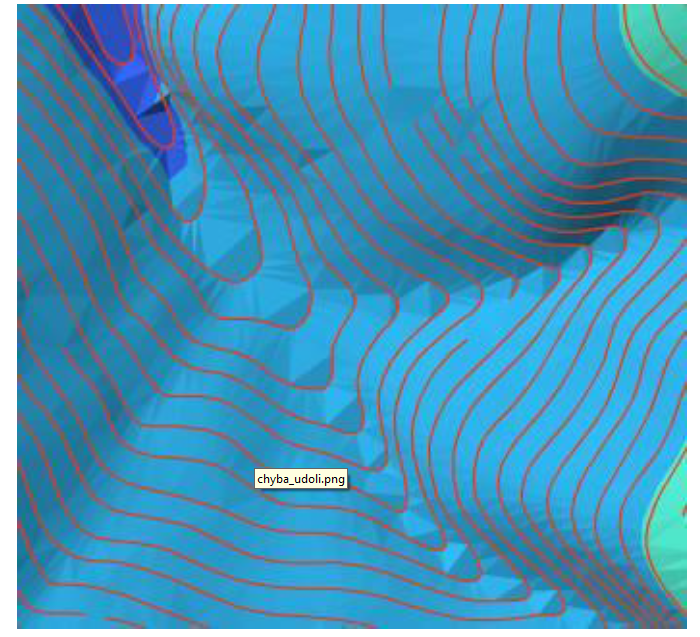
Obrázek 10: “Schody” vzniklé v údolí (zdroj: Pacina, Brejcha, 2014)

Vytvoření modelu terénu metodou TIN

TIN lze vytvořit buď konverzí z jiného typu DMT nebo z původních vrstev se zdrojovými daty (s výškovými měřeními).

Konverze z rastrového modelu do TIN je žádoucí například potřebujeme-li zpřesnit model dodáním vybraných prvků (vodní toky, silnice). Raster to TIN je nástroj, který slouží k tomuto převodu. Nativní formát ESRI Terrain, což je reprezentace modelu terénu zohledňující víceměřítkové vykreslování, je pak možné transformovat do TIN za pomoci geoprocesingové funkce Terrain to TIN.

Vytvoření nového TIN modelu ze zdrojových dat s původními měřeními nadmořských výšek je druhou možností. Funkce Create TIN je nástrojem platformy ArcGIS for Desktop pro vytváření TIN modelu terénu z vektorových dat.

Zdrojovými daty mohou být body, linie či polygony s údajem o naměřené nadmořské výšce. Body (označované jako mass points) reprezentují bodová měření, linie (breaklines) typicky prvky terénu jako řeky, hřbetnice údolnice, nebo obecně zlomové hrany v průběhu terénu. Plochy (polygony, hulls) je možné využít k vymezení oblasti, v níž má triangulace proběhnout.

Vstupní data pro TIN:

Mass points – neuspořádaná množina výškových bodů. Primární vstup do triangulace, který definuje výsledný tvar modelu terénu, bodová měření se stávají uzly ve výsledném TINu.
Hard breaklines – zlomové linie v povrchu, reprezentují diskontinuitu v průběhu terénu. Zářez v terénu způsobený takovou linií, např. vodním tokem, nebo krajnicí silniční komunikace, lze zahrnout do triangulace jejich definováním jako “hard breaklines”. Tímto lze docílit zlepšení kvality grafického znázornění modelu i kvality analýz nad ním prováděných.
Soft breaklines jsou linie na povrchu, které neovlivňují jeho tvar (nemění sklon v daném místě). Díky jejich přidání jsou do triangulace doplněny hrany odpovídající linii, jako např. hranice zkoumané oblasti.
Hulls – polygony reprezentující plošné jednotky, např. jezera, nebo hranice vymezující oblasti, které budou triangulovány odděleně. Lze využít k definování jednotlivých oblastí (ostrovů v souostroví).

Hard breaklines, soft breaklines a hulls mohou i nemusí nést informaci o nadmořské výšce. Pokud ji daná vektorová vrstva nemá, je výška interpolována z modelu vytvořeném z dat, která ji nesou.

Kromě bodových a liniových vstupních vrstev mohou vstupovat do tvorby TINu i čtyři typy plošných vrstev:

Clip polygons – definují vymezení vnější hranice celé triangulované oblasti. Oblasti, které spadají vně vymezené oblasti, jsou vyloučeny z interpolace a analýz nad výsledným modelem.
Erase polygons – definují hranici triangulace. Oblasti, které spadají dovnitř vymezené oblasti, jsou vyloučeny z interpolace a analýz nad výsledným modelem.
Replace polygons – nastavují hraniční a vnitřní výšky oblasti na konstantní hodnotu. Tedy vytváří zarovnaný povrch, např. vodorovná vodní hladina.
Fill polygons – nastavují celočíselnou hodnotu atributu každé trojúhelníkové plošce spadající do oblasti definované fill polygonem. Výšky povrchu nijak neovlivňuje.

Obrázek 11: Vliv breaklines na výslednou podobu TIN (zdroj: Pacina, Brejcha, 2014)

Matematicky spočívá konstrukce polyedrického modelu v proložení každého trojúhelníku \(t\) rovinou \(\tau\):

\[\tau: z=ax+by+c\].

Koeficienty \(a,b,c\) představují složky normálového vektoru roviny \(\tau\):

\[a=\frac{\left| \begin{array}{ccc} y_{1} & z_{1} & 1 \\ y_{2} & z_{2} & 1 \\ y_{3} & z_{3} & 1 \\ \end{array} \right|}{\left|\begin{array}{ccc} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{array}\right|}, b=\frac{\left|\begin{array}{ccc} x_{1} & z_{1} & 1 \\ x_{2} & z_{2} & 1 \\ x_{3} & z_{3} & 1 \\ \end{array}\right|}{\left|\begin{array}{ccc} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{array}\right|}, c=\frac{\left|\begin{array}{ccc} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{array}\right|}{\left|\begin{array}{ccc} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \\ \end{array}\right|},\]

kde \(P_{1}[x_{1},y_{1},z_{1}]\), \(P_{2}[x_{2},y_{2},z_{2}]\), \(P_{3}[x_{3},y_{2},z_{3}]\) jsou vrcholy daného trojúhelníku \(t\). Rovnice jednotlivých rovin nejsou udržovány v paměti, jsou podle potřeby operativně určovány (on the fly), což představuje výhodu pro práci s rozsáhlými modely.

Tipy a triky

TIN, který je určený k provádění dalších analýz, by měl být konstruován v souřadnicovém systému rovinného zobrazení. Funkce jako Slope, Aspect atp. vedou k chybným výsledkům, pokud x,y souřadnice jsou vyjádřeny úhlovou mírou (stupně v případě geografických souřadnicových systémů).

Omezení na velikost vstupních dat, tedy i výsledného počtu uzlů TIN, jsou dána systémovým množstvím dostupné paměti. Deset až patnáct milionů uzlů je obvykle horní hranice dostupná na 32-bitových platformách OS Windows. S ohledem na rychlost vykreslování je vhodné pro dataset s množstvím uzlů větším než deset milionů použít Terrain dataset namísto TIN.

3.3.2.2 Rastrový model terénu

Dalším velmi rozšířeným typem kompletní reprezentace povrchu je rastr. Základním stavebním prvkem rastrové struktury je buňka (cell, pixel). Buňky jsou organizovány do mozaiky a obsahují hodnoty, které reprezentují daný jev. U rastrů se používá několik tvarů buněk – čtyřúhelníková, trojúhelníková a hexagonální. Tyto reprezentace mají jasně definovanou topologii (víme přesně, která buňka sousedí se kterou). Nejčastěji se budeme setkávat s pravidelným čtvercovým rastrem, protože tato reprezentace je jednoduchá a je orientovaná souladu s kartézským souřadnicovým systémem. Každý rastr má také definované rozlišení (velikost buňky), které udává, jak velké skutečné území jednotlivá buňka reprezentuje.

Rastr se obecně využívá k reprezentaci spojitého jevu nad definovanou oblastí. Může se tedy jednat o DMR a z něj odvozené povrchy (sklon, orientace, křivosti, …), ale také např. o mapu znečištění ovzduší, srážky, průměrnou teplotu nebo také např. dopravní dostupnost vybraných oblastí.

Vlastnosti rastrového modelu:

Body mají mezi seboukonstantní rozestupy, snadnámanipulaci s buňkami rastru.Lépe se nad ním realizujívýpočty (interpolace).
Volba bodů se nepřizpůsobujeskutečnému tvaru terénu, vněkterých místech může býtjejich počet nadbytečný, jindenaopak nedostatečný.
Rastrový model DMT poskytuje ve většině případů horší výsledky než polyedrický model.

Základní porovnání vlastností polyedrického a rastrového modelu obsahuje tabulka 3.

Tabulka 3: Porovnání vlastností TIN a rastru

typ	TIN	rastr
výhody	schopnost popisu povrchu v různých úrovních rozlišení, efektivita v ukládání dat	jednoduchý na ukládání a k analýzám, jednoduchá integrace s rastrovými databázemi
nevýhody	v mnoha případech vyžaduje vizuální inspekci a manuální kontrolu sítě	nemožnost použití různé velikosti buněk k vyjádření povrchu s různou komplexností

(zdroj: ET Solution Center)

3.3.2.3 Plátový model terénu

U předchozích modelů mezi sousedními ploškami jsou vždy ostré přechody.Z estetického hlediska takový způsob reprezentace terénu nepůsobípřirozeně, z kartografického hlediska není věrný.Plátový model odstraňuje nevýhody předchozích modelů, vymodelovanýterén může být hladký.

Charakteristika plátového modelu:

Vyhlazení modelu v místech, ve kterých je hladký i původní terén.
Každou z plošek je proložen hladký plát.
Napojení plátů je ostré či hladké.

Plátový model nad polyedrickým modelem je tvořen pláty trojúhelníkového tvaru, plátový model nad rastrovým modelem pak pláty čtvercového tvaru (obrázek 12).

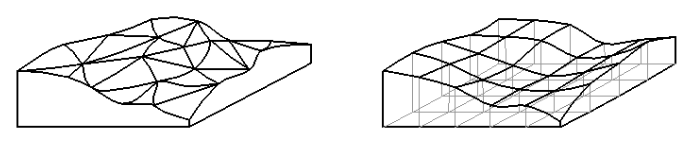
Obrázek 12: Plátový model (zdroj: http://k154.fsv.cvut.cz/~stroner/GEY2/pred_4_Metrologie_DMT.pdf)

Konstrukce vrstevnic interpolací

V praxi jsou využívány lineární i nelineární interpolační algoritmy:

lineární - spád terénu mezi dvěma body, mezi kterými provádíme interpolaci, je konstantní. Rozestup vrstevnic mezi dvěma body je také konstantní. Výpočetně jednoduché, ale nevystihuje realitu.
nelineární - mezi interpolovanými body předpokládáme plynulou změnu sklonu terénu - geomorfologická interpolace. Rozestup vrstevnic mezi dvěma body není konstantní. Zohledňuje skutečný tvar terénu (sklon okolních plošek). Využívají kvadratické či kubické interpolace. Používá se v mapách velkých a středních měřítek. Postup je značně složitý a obtížně se algoritmizuje.

Konstrukce vrstevnic lineární interpolací vychází také z analytické geometrie. Je-li dána rovina plátu \(\tau(P_1,P_2,P_3)\) a rovina \(\rho: z=h\), pak hledáme průsečnici \(AB\) roviny \(\tau\) trojúhelníku \(t\) a vodorovné roviny s výškou \(h\) (výška vrstevnice). Tuto úlohu je nutno opakovat na všemi trojúhelníky \(t\). Princip znázorňuje obrázek 13.

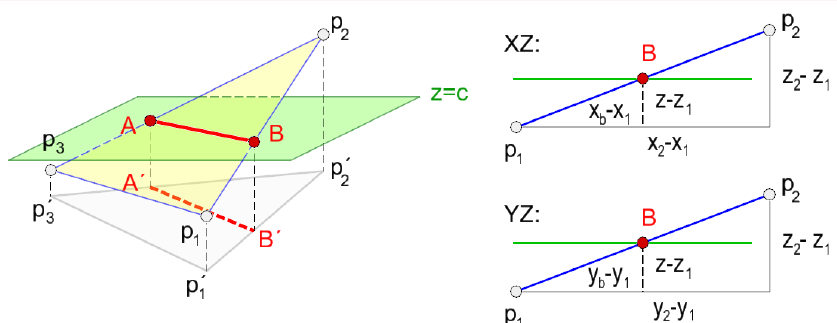
Obrázek 13: Lineární interpolace vrstevnic (zdroj: Bayer, 2016)

Výpočet souřadnic bodů \(A,B\) průsečnice pak závisí na vzájemné poloze \(\tau\) a \(\rho\): nemají-li žádný společný bod nebo jeden společný bod, neřešíme; zajímá nás situace, kde je průsečnicí úsečka.

Z podobnosti trojúhelníků představujících průměty do roviny \(XZ\) a \(YZ\) platí:

\[\begin{array}{cc} \frac{x_2-x_1}{z_2-z_1}=\frac{x_b-x_1}{z-z_1} & \frac{y_2-y_1}{z_2-z_1}=\frac{y_b-y_1}{z-z_1} \\ \frac{x_3-x_1}{z_3-z_1}=\frac{x_a-x_1}{z-z_1} & \frac{y_2-y_1}{z_2-z_1}=\frac{y_a-y_1}{z-z_1} \\ \end{array}.\]

Výsledné souřadnice bodů \(A,B\) průsečnice určíme ze vztahů:

\[\begin{array}{cc} x_a=\frac{x_3-x_1}{z_3-z_1}(z-z_1)+x_1, & x_b=\frac{x_2-x_1}{z_2-z_1}(z-z_1)+x_1 \\ y_a=\frac{y_3-y_1}{z_3-z_1}(z-z_1)+y_1, & y_b=\frac{y_2-y_1}{z_2-z_1}(z-z_1)+y_1 \\ \end{array}\] Test, zda rovina \(\rho\) protíná stranu \((P_i,P_{i+1})\) trojúhelníku:

\[(z-z_i)(z-z_{i+1})<0\].

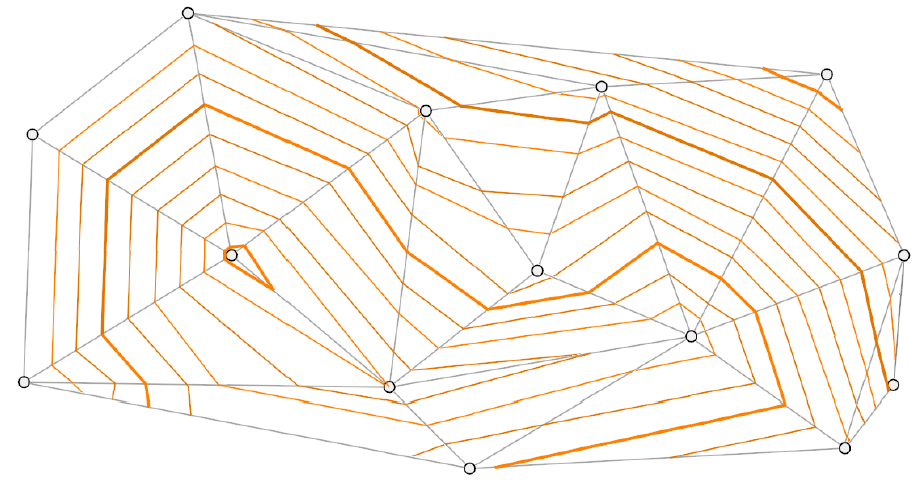
Obrázek 14: Ukázka výpočtu vrstevnic lineární interpolací (zdroj: Bayer, 2016)