Kapitola 4 Analýzy povrchů

Využití digitálních modelů terénu (DMT) a dalších povrchů je v současnosti velmi rozsáhlé díky snadné dostupnosti jak zdrojových dat pro jejich tvorbu, tak i softwarových nástrojů pro jejich analýzu. V této kapitole se podíváme nejprve na vybrané metody analýzy povrchu samotného a poté i na analýzy prováděné nad modelem takového povrchu.

Při řešení mnoha problémů v prostorové analýze je potřeba využívat prostorově rozsáhlá data - informace o atributech, které lze v zásadě měřit na všech místech v definované oblasti. Velká část výzkumu v této oblasti pramení z práce v terénu - modelování formy povrchů z omezených údajů vzorku pomocí interpolačních technik, zkoumání toku materiálů a vody přes povrchy a vyhodnocování linií a tras pozorování krajin. Stejné koncepty se však vztahují na jakýkoli soubor dat, který má atribut s jednou hodnotou (obvykle pozitivní) měřitelný na každém místě studované oblasti - teplota, tlak, vlhkost, stopové prvky v půdě a mnoho dalších proměnných tohoto typu. Kromě toho existuje celá řada případů, kdy je třeba pro účely srovnání nastavit intenzitní proměnné (např. data bodových událostí, počty uvnitř zón atd.) V kontextu prostorově rozsáhlých dat.

V této kapitole se budeme zabývat následujícími typy analýz povrchů:

• morfometrické analýzy povrchů,
• problematika viditelnosti,
• hydrologické modelování,
• analýzy vhodnosti,
• distanční modelování.

Do první skupiny patří morfometrické analýzy povrchů. Krcho (1990) uvádí následující hlavní morfometrické analýzy charakteristik povrchu:

• sklon ve směru spádové křivky,
• orientace,
• normálová křivost,
• horizontální křivost.

Tyto parametry povrchu bývají definovány prostřednictvím metod diferenciální geometrie. Podrobné informace k této tematice lze nalézt např. v již zmíněném Krcho (1990). V teoretickém úvodu z tohoto zdroje vyjdeme při připomenutí základních pojmů. Z prostorových analýz, prováděných s využitím DMT, se budeme věnovat výškovým profilům, osvětlení reliéfu a analýze viditelnosti.

Výše uvedené analýzy mají množství praktických aplikací v oblasti územního plánování, prostupnosti terénu, hydrologii, krizovém managementu, plánování v oblasti telekomunikací, redukce hluku, či hodnocení scénické kvality jak pro civilní, tak i vojenské potřeby.

4.1 Morfometrické charakteristiky

Topografický povrch (nadmořskou výšku \(z\) pro \(x,y\)-souřadnice) lze vyjádřit spojitou funkcí dvou proměnných \(f(x,y)\). Budeme používat první derivaei dle jednotlivých proměnných (souřadnic) \(x\) a \(y\)

\(f_x=\frac{\partial f}{\partial x}\) a \(f_y=\frac{\partial f}{\partial y}\)

a druhé derivace

\(f_{xx}=\frac{\partial^{2}f}{\partial x^{2}}\), \(f_{yy}=\frac{\partial^{2}f}{\partial y^{2}}\) a \(f_{xy}=\frac{\partial^{2}f}{\partial x\partial y}\).

Pomocí parciálních derivací získáme tzv. odvozené morfometrické charakteristiky povrchu:

Gradient

Gradient (tj. vektor max. spádu) \(\nabla f(x_0,y_0)\) funkce \(f(x,y)\) v bodě \(P[x_0,y_0]\) má směr normály k vrstevnici a je orientovaný ve směru růstu funkce \(f\). Jeho souřadnice jsou určeny parciálními derivacemi \(f_x\) a \(f_y\) v bodě \(P[x_0,y_0]\):

\(\nabla f(x_0,y_0)=(f_x,f_y)\).

Sklon svahu (Slope)

Běžná představa sklonu povrchu nebo terénu \(t\) je úroveň stoupání (např. Změna nadmořské výšky) během pohybu v nějakém směru, obvykle směr, pro který je stoupání během pohybu největší, tj. Nejstrmější cesta nahoru nebo dolů (ve směru spádnice). V praxi bychom specifikovali určitou vzdálenost, přes kterou se má vypočítat sklon, jako je například výška stoupání na vzdálenost 10 metrů v rovině. Pokud by to například byly 2 metry, byl by nárůst při pohybu \(S = 2: 10\) nebo \(1: 5\) nebo 0,2 či 20%. Tento poměr lze vyjádřit jako rovnici tečny: \(S = \tan (S_t)\), kde \(S_t\) je sklon terénu v radiánech. Pokud bychom uvažovali pohyb ve smyslu vzdálenosti povrchu spíše než vzdálenosti roviny, pak bychom jej vyjádřili jako \(S = \sin (S_t)\). Pro mírné svahy (méně než 1: 4) není tato nejednoznačnost v definici sklonu vážná, ale obecně je preferována funkce \(\tan\).

V programech GIS se sklon obvykle vyjadřuje jako \(S = \tan (S_t)\) ve stupních od horizonátlní roviny. Převod mezi obloukovou a stupňovou mírou tedy provedeme podle vztahu:

\(S_t=\arctan (S)[^{o}]=\frac{360\arctan (S)}{2\pi} [rad]\).

Sklon v libovolném bodě \(P[x_0,y_0]\) je tedy úhel mezi tečnou rovinou k ploše v bodě \(P[x_0,y_0]\) a rovinou rovnoběžnou s rovinou \((x,y)\) ve směru spádnicové křivky. Pro sklon platí:

\(\sigma=\arctan \sqrt{f^{2}_{x}+f^{2}_{y}}\). (1)

Orientace svahu (Aspect)

Orientace svahu popisuje orientaci povrchu vůči světovým stranám. Vyjadřuje se ve stupních v rozsahu 0–360 stupňů, není definována v singulárních bodech (vrchol, sedlo, atp.). Orientace v bodě je definována jako azimut průmětu gradientu \(\nabla\) do roviny \(f(x,y)\) a pro její hodnotu platí:

\(\alpha=\arctan (\frac{f_y}{f_x})\). (2)

Normálová křivost (Profile Curvature)

Křivost normálového řezu ke zkoumané křivce ve směru tečny je dána vztahem:

\(\omega=\frac{f_{xx}f^{2}_{x}+2f_{xy}f_{x}f_{y}+f_{yy}f^{2}_{y}}{(f^{2}_{x}+f^{2}_{y})\sqrt{1+f^{2}_{x}+f^{2}_{y}}}\). (3)

Zjednodušeně je možné říci, že normálovou křivostí se rozumí křivost normálového řezu bodě \(A[x,y]\) jako průsečnici plochy s rovinou obsahující normálu \(N\) k topografické ploše a tečny \(n\) ke spádnici, tak že rovina řezu je kolmá na tečnou rovinu k topografické ploše v daném bodě \(A[x,y]\).

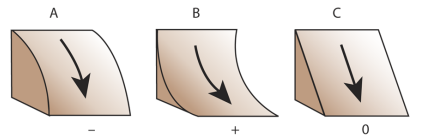
Obrázek 1: Normálová křivost (zdroj: https://pro.arcgis.com/en/pro-app/help/data/imagery/curvature-function.htm)

Právě s pomocí hodnoty normálové křivosti můžeme charakterizovat jednotlivé morfometrické formy georeliéfu. Tyto formy jsou od sebe odděleny inflexními body s \(\omega = 0\). Pokud je \(\omega > 0\), pak forma je konvexní (vypouklá) a pokud \(\omega < 0\), tak je forma konkávní (dutá).

Pro úplnost musíme ještě připomenout, že platí:

\(\omega=K_n=\frac{1}{R_{\omega}}\),

kde \(R_{\omega}\) je poloměr normálové křivosti. Tímto poloměrem je v bodě \(A[x,y]\) opsána kružnice normálové křivosti se středem na normále \(N\). Kružnice leží v rovině normálového řezu (obrázek 2).

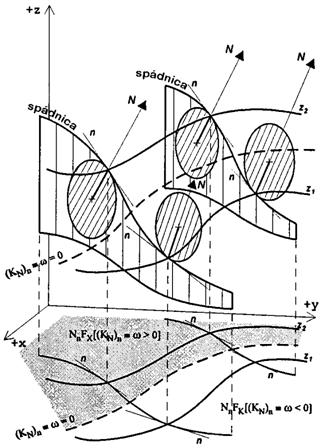
Obrázek 2: Normálová křivost - odvození (zdroj: převzato z Krcho, 1990)

Povrch lze samozřejmě vyjádřit pomocí izočár křivostí. Pokud budeme \(\omega\) brát jako proměnný parametr tak pro \(\omega > 0\) nazveme izočáry normálové izokonvexy, pro \(\omega < 0\) normálové izokonkávy a pro \(\omega = 0\) izočárou nulové normálové křivosti. Právě ta poslední izočára nám ukazuje, kde jsou hranice forem. Pro odvození a důkaz platnosti vztahů výše viz Krcho (1990).

Horizontální křivost (Plan curvature)

Poloměr horizontální křivosti \(R_k\) je svislým průmětem poloměru normálové křivosti do roviny horizontálního řezu. A tak je poloměr kružnice vrstevnice \(R_k\) je vzhledem na velikost poloměru \(R_n\) ležícího v normále určený vztahem:

\(\frac{R_k}{R_n}=\sin \gamma_n\), tj. \(R_k=R_n \sin \gamma_n\).

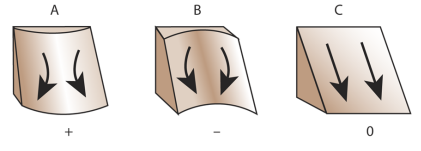
Obrázek 3: Horizontální křivost (zdroj: https://pro.arcgis.com/en/pro-app/help/data/imagery/curvature-function.htm)

Vyjádřeno pomocí parciálních derivací má vztah pro horizontální křivost tento tvar:

\(K_r=-\frac{f_{xx}f^{2}_{y}+2f_{xy}f_{x}f_{y}+f_{yy}f^{2}_{y}}{\sqrt{1+f^{2}_{x}+f^{2}_{y}}}\).

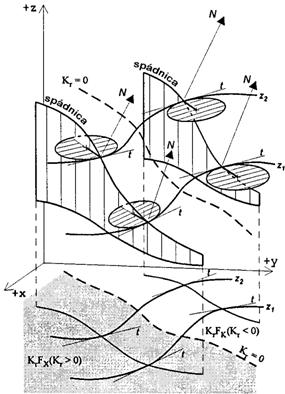
Obrázek 4: Horizontální křivost (zdroj: převzato z Krcho, 1990)

Tato křivost nabývá kladných a záporných hodnot a jsou prostorově stejně rozložené v rovině \((x,y)\). Jen se liší velikostí závislosti od úhlu sklonu \(\gamma_n\). Hodnota horizontální křivosti se mění na základě hodnot \(x\) a \(y\), tím pádem je funkcí polohy. Podobně jako u normálových křivostí jsou horizontální formy reliéfu konvexní tam, kde \(K_r > 0\) a konkávní, kde \(K_r < 0\). Kružnice křivosti má jeden konstantní poloměr jako převrácenou hodnotu \(R_k\). V konvexních formách leží kružnice křivosti na vnitřní straně a u konkávních formách na vnější straně. Situace je znázorněna na obrázku 2.

4.2 Metody výpočtu morfometrických charakteristik v GIS

Matematické modely ploch jsou sice široce používány v procesu odvozování hodnot parametrů zemského povrchu, přesto je typickou reprezentací dat, nad níž jsou analýzy implementovány, pravidelná mřížka pixelů (rastr). I když tato reprezentace nemá eleganci a kompaktnost matematického modelu, velmi dobře se hodí pro počítačové analýzy. Ve výsledku jsou téměř všechny analýzy povrchu v GIS prováděny nad rastrovou reprezentací, spíše než ve formě čistě geometrického zpracování. Rastrová reprezentace při analýzách povrchu dostává často přednost i před formou nepravidelné trojúhelníkové sítě (TIN).

Koncepčně nástroje nad rastry využívají tzv. masku, tedy matici 3×3 pixelů tvořících okolí osmi pixelů zkoumaného pixelu (obrázek 3):

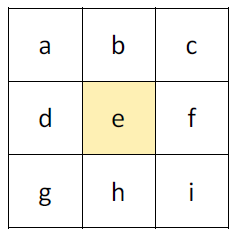
Obrázek 3: Maska 3x3 pixelů (zdroj: ESRI Help, 2016)

Změna výšky (reprezentována hodnotou pixelu) ve směru \(x\) se v ArcGIS for Desktop získává následujícím způsobem:

\(f_x=\frac{(c+2f+i)-(a+2d+g)}{8*x_{cellsize}}\),

analogicky ve směru \(y\):

\(f_y=\frac{(g+2h+i)-(a+2b+c)}{8*y_{cellsize}}\).

4.2.1 Výpočet sklonu (Slope)

S takto definovanými \(f_x\) a \(f_y\) odpovídá sklon měřený v radiánech rovnici (1).

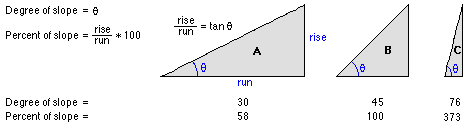
Obrázek 4: Dvě možnosti vyjádření sklonu (zdroj: ESRI Help, 2016)

4.2.2 Výpočet orientace (Aspect)

S takto definovanými \(f_x\) a \(f_y\) odpovídá orientace měřená v radiánech rovnici (2).

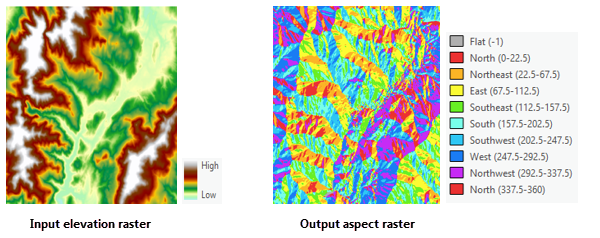
Obrázek 5: Orientace svahu vůči světovým stranám (zdroj: ESRI Help, 2016)

4.2.3 Výpočet křivosti

Hodnota křivosti je počítána s využitím druhých derivací vstupního povrchu, viz rovnice (3), který je získán z hodnot matice 3×3 okolí zkoumaného bodu následujícím způsobem (ESRI Help, 2016):

\(Z=Ax^{2}y^{2}+Bx^{2}y+Cxy^{2}+Dx^{2}+Ey^{2}+Fxy+Gx+Hy+I\),

kde: \[\begin{eqnarray} % \nonumber to remove numbering (before each equation) A &=& [(Z_1+Z_3+Z_7+Z_9)/4-(Z_2+Z_4+Z_6+Z_8)/2+Z_5]/L^{4} \\ B &=& [(Z_1+Z_3-Z_7-Z_9)/4-(Z_2-Z_8)/2]/L^{3} \\ C &=& [(-Z_1+Z_3-Z_7+Z_9)/4-(Z_4-Z_6)/2]/L^{3} \\ D &=& [(Z_4+Z_6)/2-Z_5]/L^{2} \\ E &=& [(Z_2+Z_8)/2-Z_5]/L^{2} \\ F &=& (-Z_1+Z_3+Z_7-Z_9)/4L^{2} \\ G &=& (-Z_4+Z_6)/2L \\ H &=& (Z_2-Z_8)/2L \\ I &=& Z_5 \end{eqnarray}\]

Proměnné \(L, Z_1, Z_2,\) atd. odpovídají obrázku 4 (ESRI Help, 2016).

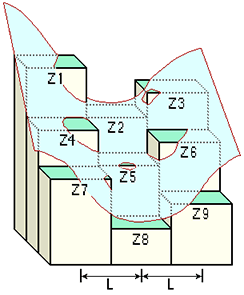
Obrázek 6: Princip výpočtu křivosti plochy (zdroj: ESRI Help, 2016)

Výstupy nástrojů mohou být z hlediska aplikací použity například pro popis fyzikálních charakteristik povodí ve snaze pochopit průběh eroze či odtokové procesy. Sklon ovlivňuje zrychlení. Orientace určuje směr proudění. Profil zakřivení ovlivňuje změny ve zrychlení, resp. zpomalení toku, a tudíž ovlivňuje erozi, resp. ukládání materiálu.

Poznámka: výpočty na TIN probíhají na stejných teoretických základech, pouze zvlášť pro každou plochu TIN povrchu.

ArcGIS Pro umožňuje výpočet normálové i horizontální křivosti (obrázky 1 a 3). Zároveň pracuje i s tzv. standardní křivostí, která je kombinací křivosti normálové i horizontální. Normálová křivost ovlivňuje zrychlení a zpomalení toku, a proto ovlivňuje erozi a depozici materiálu na povrchu. Horizontální křivost ovlivňuje konvergenci a divergenci pohybu (toku). Zohlednění obou křivostí současně umožňuje přesnější porozumění pohybu po povrchu.

Na obrázku 7 odpovídají sloupce horizontální křivosti a řádky křivosti normálové. Kladné, záporné a nulové hodnoty horizontální křivosti lze sledovat zleva doprava. Normálové křivosti jsou negativní, pozitivní a 0 směrem shora dolů.

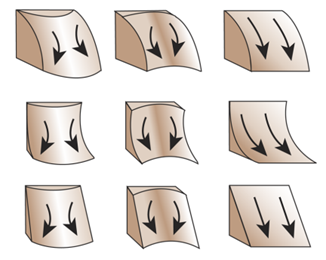
Obrázek 7: Standardní křivost plochy (zdroj: https://pro.arcgis.com/en/pro-app/help/data/imagery/curvature-function.htm)

4.2.4 Stínování reliéfu (Hillshade)

Analýza osvětlení modelu povrchu kvantifikuje množství dopadajícího světla na dané místo. Výsledná hodnota je spočtena prostorovou syntézou úhlu sklonu a orientace reliéfu, výškou Slunce nad obzorem a azimutem Slunce.

Nástroj Hillshade softwaru ArcGIS for Desktop počítá hodnotu stínovaného reliéfu následujícím způsobem (ESRI Help, 2016):

Hillshade=255.0((cos(Zenith_rad)cos(Slope_rad)+(sin(Zenith_rad)sin(Slope_rad)cos(Azimuth_rad-Aspect_rad)),

kde jsou orientace a sklonitost v radiánech získány postupy uvedenými výše.

S využitím Hillshade lze docílit vizuálně atraktivní prezentace modelů terénu. Hillshade analýzou lze též zjistit zastínění daného místa pro konkrétní datum a čas.

Obrázek 8: Hillshade - výsledný rastr vytvořený z LIDAR DEM (zdroj: https://gis.stackexchange.com)

4.2.5 Analýza viditelnosti

Základem analýz viditelnosti je určení bodů, které jsou ze zkoumaného bodu viditelné a které nikoli. Generování viditelnosti je založeno na digitálním výškovém modelu.Viditelnost v GIS je většinou řešena na zvolené úsečce nebo ve vybrané ploše (v oblastech počítačové grafiky většinou spíše pro definovaný zorný úhel). Funkce viditelnosti nejprve sestaví rovnice spojnice testovaného místa s místem pozorování. V každém mezilehlém pixelu, kterým spojnice prochází, je testována jeho výška s výškou spojnice v daném místě. Výsledkem aplikace analýzy je datový soubor, do něhož jsou zařazeny pixely viditelné (ty, jejichž spojnice má ve všech místech výšku vyšší) a neviditelné (alespoň v jednom místě spojnice nižší výšku než povrch, nad kterým analýza probíhá). Funkce viditelnosti je používaným nástrojem i pro opačně definovanou úlohu, tedy plánování umístění objektů na zemský povrch.

V ArcGIS for Desktop obsahuje Visibility toolset následující nástroje:

• Viewshed – určuje oblasti viditelné z množiny pozorovacích míst definovaných pomocí bodové či polyliniové vrstvy. Nástroj umožňuje zadat zorný úhel, ve kterém analýza proběhne, a to jak v horizontálním, tak ve vertikálním směru. Dalšími parametry nástroje je offset, tedy definice hodnoty výšky nad povrchem, pro kterou analýza proběhne. Lze zadat pro pixely odpovídající jak pozorovateli, tak i cílovému území. Nadto je v nastavení nástroje možné vybrat, zda analýza bude počítat se zemským zakřivením případně s refrakcí světelného záření, nebo nikoli.

Obrázek 9: Viewshed - viditelná část povrchu (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/using-viewshed-and-observer-points-for-visibility.htm)

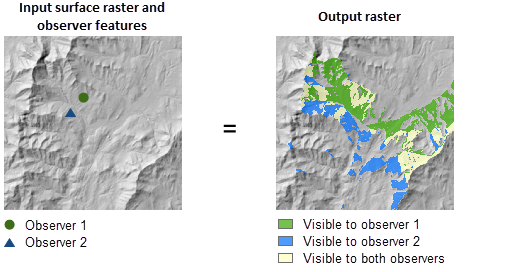
Obrázek 10: Viewshed2 - viditelná část povrchu pro více pozorovatelů (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/using-viewshed-and-observer-points-for-visibility.htm)

• Visibility – rozšiřuje funčnost nástroje Viewshed. Kromě určení oblastí viditelných z množiny pozorovacích míst (analysis type: Frequency - ve výsledném rastru nesen počet pozorovacích míst, z nichž viditelný) může také určit, která konkréktní pozorovací místa jsou viditelná z každé polohy (pixelu) na rastru povrchu (analysis type: Observers).

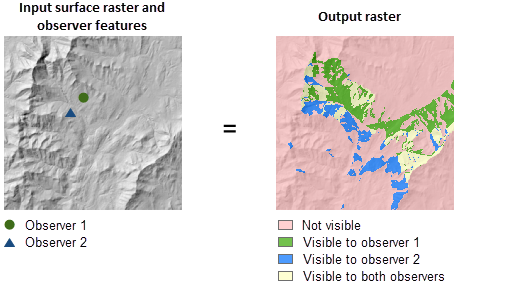
Obrázek 11: Visibility - viditelná část povrchu pro více pozorovatelů (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/using-viewshed-and-observer-points-for-visibility.htm)

• Line of Sight a Intervisibility – tyto nástroje umožňují určit viditelnost podél definované linie vzhledem k překážkám, kterými mohou být kromě samotného povrchu i další objekty na něm definované. Datové typy překážek zahrnují body, linie polygony, multipatch, raster i TIN.

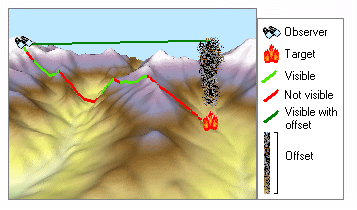
Obrázek 12: Line of Sight - viditelnost podél definované linie (zdroj: https://desktop.arcgis.com/fr/arcmap/latest/analyze/commonly-used-tools/surface-creation-and-analysis.htm)

• Skyline – analyzuje linii horizontu. Tento nástroj generuje 3D polylinii, která odděluje nebe od povrchu a objektů v okolí pozorovatele. V kombinaci s nástrojem Skyline Barrier umožňuje na základě siluety odvodit objem stínu vrženého vybraným objektem, či analyzovat, zda zařazení nového objektu (výstavba nové budovy) změní původní linii obzoru. Dalšími aplikacemi mohou být analýzy překážek či hrozeb pro danou leteckou cestu ve 3D či návrh úpravy leteckého koridoru.

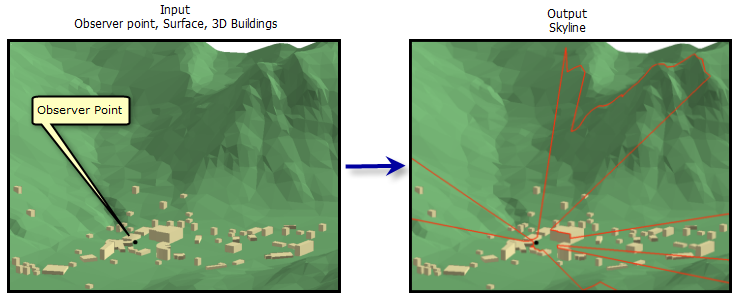
Obrázek 13: Skyline - linie horizontu (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/3d-analyst/skyline.htm)

4.3 Hydrologické analýzy

Další velmi rozšířenou aplikací DMT jsou hydrologické analýzy. Informace o tvaru zemského povrchu jsou užitečné pro mnoho oblastí, jako je regionální plánování, zemědělství a lesnictví. Odborníci v těchto oblastech se snaží pochopit to, jakým způsobem se voda v dané oblasti pohybuje a jak změny v oblasti mohou ovlivnit tyto toky. Vstupem pro tento druh analýz je obvykle DMT.

Pro hydrologické analýzy je zapotřebí vytvořit hydrologicky korektní DMT – musí být odstraněny sníženiny, které vznikly jako artefakt interpolace vstupních dat. Ponechání těchto sníženin by mělo za následek zkreslení hydrologických analýz (voda vteče do sníženiny a dále neteče). Sníženiny (a vrcholy) jsou časté chyby vzniklé v důsledku nevhodného rozlišení dat nebo zaokrouhlování výšek na nejbližší celé číslo. Sníženiny by měly být zaplněny, aby se zajistilo správné vymezení povodí a toků. Pokud nejsou zaplněny, může dojít k tomu, že modelovaná říční (odtoková) síť bude nespojitá.

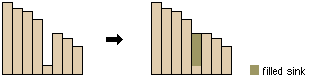
Obrázek 14: Fill - vyplňování sníženin DMT (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/how-fill-works.htm)

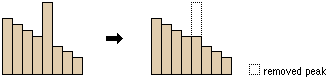
Obrázek 15: Fill - odstranění vyvýšenin DMT (zdroj: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/how-fill-works.htm)

Princip tvorby povodí ukazuje obrázek 16. Z rastru nadmořských výšek je vypočítán rastr směru odtoku z buňky. Voda odtéká jedním z 8 možných směrů do sousední buňky s nejnižší nadmořskou výškou (tzv. D8 algoritmus12). Z tohoto rastru se odvodí rastr akumulace vody (počet buněk, které do dané buňky vtékají). Z rastru akumulace vody se vytvoří rastr vodních toků, dle následující stanovené podmínky – pokud do dané buňky vtéká voda zvíce jak 2 buňek už je to vodní tok. Z rastru vodních toků a rastru akumulace se vytvoří rastr povodí.

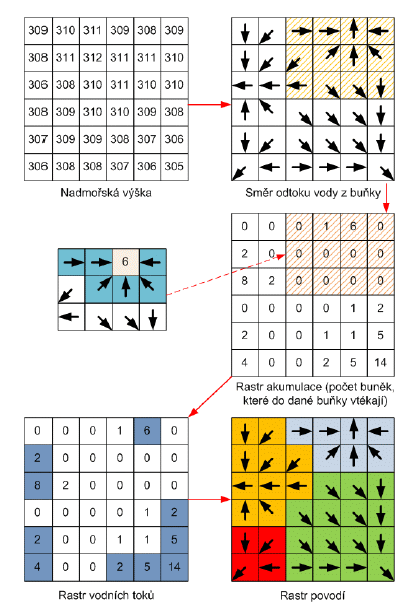
Obrázek 16: Princip výpočtu povodí (zdroj: Pacina, Brejcha, 2014)

4.4 Analýzy vhodnosti (Suitability Analysis)

Cílem těchto analýz je nalezení vhodné lokace pro umístění nového zařízení na základě předem zvolených kritérií. Toho lze dosáhnout kombinováním a odvozováním vrstev prostorových dat pomocí různých typů prostorových analýz. Mezi nejčastěji používané patří například:

• vzdálenostní analýzy (přímá vzdálenost, vážená vzdálenost, nekratší cesta, …),
• analýzy povrchu (svahovitost, směry svahů, viditelnost, …),
• určování hustoty bodů a linií,
• interpolace (IDW, Kriging, Spline),
• mapová algebra (mocný nástroj umožňující různé operace s vrstvami pomocí matematických operátorů),
• reklasifikace a další.

Pro tyto typy analýz se v programu ArcGIS používají funkce nadstavby Spatial Analyst. To je rozšiřující sada funkcí, poskytující nástroje pro prostorové analýzy nad rastry i vektory. Funkce Spatial Analyst se dají využít například také pro výpočet povrchů nákladů či identifikaci prostorových vztahů mezi různými vrstvami dat.

Postup analýzy lze rozdělit do čtyř základních kroků:

1. Máme-li nadefinován problém, který je třeba vyřešit, musíme nejprve zjistit, jaká vstupní data potřebujeme, jaká máme k dispozici, případně jaká můžeme opatřit. Při výběru vstupních dat jde o hledání kompromisu mezi daty, která by byla pro analýzu nejvhodnější, a daty, která jsou dostupná. K nejdůležitějším faktorům ovlivňujícím výběr vhodných vrstev patří cena, kvalita, rozlišení a aktuálnost dat.
2. Druhým krokem je odvození rastrových vrstev, potřebných pro analýzu, ze vstupních dat. K tomu se používají různé funkce Spatial Analyst. V příkladech se seznámíme s některými z nich.
3. Poté, co získáme všechny vrstvy potřebné pro určení vhodného místa, je třeba hodnoty atributů těchto vrstev převést na společnou stupnici, aby bylo možné je objektivně propojit. Pro tyto potřeby je ve Spatial Analyst funkce Reclassify, slouží pro nahrazení hodnot buněk vstupního rastru novými hodnotami. Často se používá deset intervalů se stejnou šířkou intervalu a hodnotami od 1 do 10, kde 10 značí nejvhodnější lokaci. V případě, že hodnoty atributu nejsou číselné, ale například udávají využití půdy, přiřadíme libovolné hodnoty od 1 do 10 dle vhodnosti.
4. Poslední částí je propojení reklasifikovaných vrstev do jedné výsledné vrstvy. Jelikož mohou být jednotlivé vrstvy různě důležité pro analýzu je vhodné ohodnocení významnosti jednotlivých faktorů – váhování. To se provádí pomocí funkce Map Algebra. Používáme převážně normalizované váhy (procenta / 100), aby výsledné hodnoty byly opět v intervalu od 1 do 10. Nakonec lze obarvit vyšší hodnoty atributu vzniklé vrstvy a vizuálně ohodnotit a vybrat vhodné lokace.

4.4.1 Analýzy vhodnosti - příklad: výběr lokality vhodné pro založení vinice

Představme si tuto teoretickou úlohu – v okolí daného města chceme založit vinice. Pokusíme se vybrat oblasti splňující následující kritéria:

• orientace na jih,
• sklon svahu maximálně 15°,
• nadmořská výška maximálně 320 m n.m.

Jako vstup dat použijeme vrstevnice oblasti. Dále bychom měli uvažovat typ půdy, průměrnou teplotu, zastavěnost oblastí, vlastnické vztahy, atd. – ale s ohledem k ukázkovému řešení zaměřenému na aplikaci DMT budeme vycházet pouze ze zadaných bodů.

Postup práce:

1. Z vrstevnic vytvoříme DMT.
2. Na vytvořeném DMT provedeme analýzu sklonu (slope) a orientace (aspect).
3. Pomocí mapové algebry vybereme z vrstvy DMT, sklonu a orientace takové oblasti (buňky rastru), které splňují výše stanovená kritéria.

4.5 Vzdálenostní analýzy (Distance Modelling)

Do této skupiny patří řešení problémů na bázi vzdálenosti - např. určení nejvhodnějšího koridoru po stavbu dálnice, modelování šíření ohně, nalezení optimální trasy v divočině, modelování povodňové vlny, modelování vlivu zplodin v ovzduší a mnohé další. Na první pohled jde o jednoduchou problematiku, která se však ve spolupráci s mapovou algebrou (pro rastrovou reprezentaci), či analýzami sítí (pro vektorovou reprezentaci) může rozvinout ve velice složitý a sofistikovaný nástroj.

Bezesporu nejpoužívanějším nástrojem vzdálenostních analýz je tvorba obálky (bufferu). U rastrové reprezentace je tvorba obálky otázkou metriky. Všechny buňky, které jsou od daného objektu v menší vzdálenosti než definovaná budou označeny.

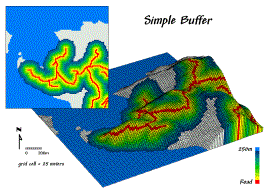
Obrázek 17: Ukázka bufferu (zdroj: http://www.innovativegis.com/basis/MapAnalysis/Topic13/Topic13.htm)

Velice často se ale v rastrové datové struktuře provádí analýza okolí tak, že se spočítá vzdálenost každé buňky od požadovaného objektu a ta vzdálenost se uloží do nové vrstvy (obrázek 18), kterou je samozřejmě možné dále reklasifikovat (např. buňky s hodnotou menší než 3km - hodnota 1, jinak hodnota “NO_DATA”). Tato analýza se často nazývá nalezení vzdálenosti (Find Distance).

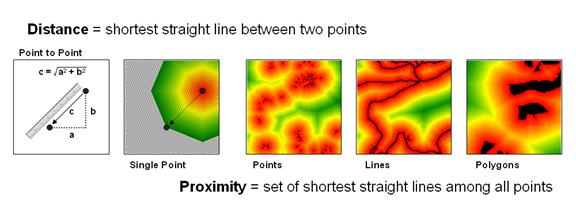
Obrázek 17: Eukleidovské vzdálenosti na rastrových datech (zdroj: http://www.innovativegis.com/basis/BeyondMappingSeries/BeyondMapping_III/Topic2/BM_III_T2.htm)

4.5.1 Analýzy sousedství (Proximity analysis)

Mezi vzdálenostní analýzy také patří takzvané analýzy sousedství (proximity analysis). Spočívají v tvorbě “individuální plochy” kolem každého ze vstupních bodů, které definují příslušnost dané lokality k nějbližším z objektů. Pro vlastní výpočet se používá metody Thiessenových polygonů nebo Voronoi diagramy, což jsou duální funkce k triangulaci. Funkci proximity analysis je možné provádět jak v rastrové, tak ve vektorové podobě.

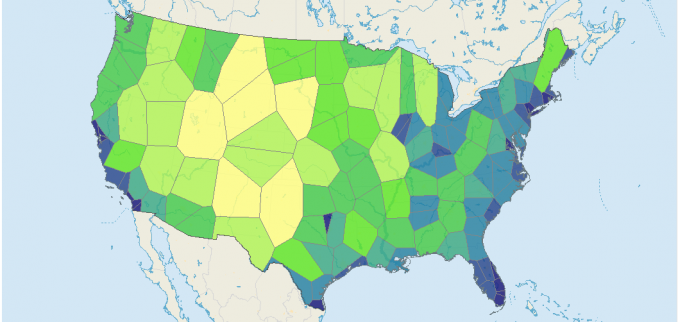
Obrázek 18: Thiessenovy polygony - Voronoi diagram (zdroj: https://gisgeography.com/voronoi-diagram-thiessen-polygons/)

4.5.2 Vážené vzdálenosti (Weighted Distances)

Další vzdálenostní analýzou je tzv. vážená vzdálenost (weighted distance). Metoda vážené vzdálenosti hledá nejméně nákladnou cestu z každé buňky do daného objektu. Nápad vychází z analýzy okolí u rastrové reprezentace (každá buňka má přiřazenou vzdálenost od požadovaného objektu). Všímá si tam ale jedné podstatné vlastnosti, a to, že při běžných vzdálenostních analýzách se všeobecně neuvažují vlivy okolí, vše je měřeno vzdušnou čarou za ideálních podmínek. V reálném světě ale tento model zdaleka neodpovídá skutečnosti. Reálná vzdálenost neodpovídá vzdálenosti “vzdušnou čarou” - má na ni vliv převýšení terénu, pohyb do kopce stojí více námahy než z kopce; bude-li proti nám foukat vítr, spotřebujeme také více pohonných hmot nebo sil apod. Tyto faktory lze do analýzy zahrnout právě pomocí vážené nebo ohodnocené vzdálenosti.

Jedním z nich může být faktor terénního reliéfu, který převádí rovinnou vzdálenost mezi buňkami na vzdálenost po reliéfu (terénní vzdálenost). Pro její výpočet jsou potřebné údaje o DMR.

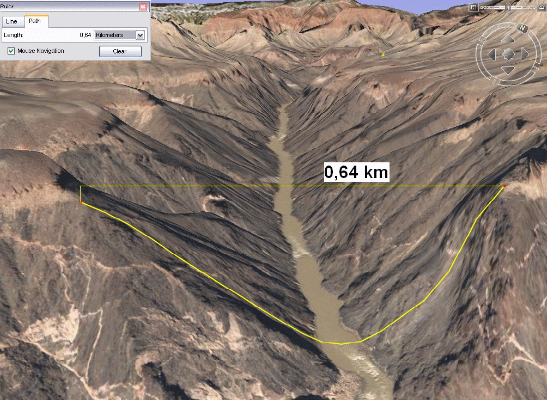
Obrázek 19: Terénní vzdálenost (zdroj: http://geomatika.kma.zcu.cz/studium/ugi/Prezentace/11-AnalyzyVzdalenostniSousedstviVazenaVzdalenostNejlevnejsiCestaGrafove.pdf)

Reálnou vzdálenost ovlivňují vlastnosti reálného světa - např.:

• objekty na povrchu (antropogenní prvky, krajiný pokryv),
• průběh terénu,
• s ním související převýšení,
• převládající směr větru,
• a další,

které jsou modelovány jako faktory ovlivňující váženou vzdálenost:

• frikční povrch - vzniká reklasifikací DMÚ (využití půdy - Land Use) podle nákladovosti na překonání jednotlivých buněk, zohledňuje objekty (antropogenní prvky, krajinný pokryv) nacházející se na povrchu;
• faktor terénního reliéfu - izotropní - nezáleží na směru pohybu - počítá se z DMR;
• vertikální faktor - anizotropní - záleží na směru pohybu - počítá se ze sklonu svahů;
• horizontální faktor - anizotropní - účinek převládajícího horizontálního směru působení faktoru na energii, kterou musíme vynaložit, abychom překonali buňku.

Tyto faktory jsou pak skládány do výsledného povrch nákladů (nákladového vzdálenostního povrchu). Povrch nákladů lze tedy charakterizovat jako povrch, jehož každá buňka ví, “jak drahé je její překonání”.

Akumulační (nákladová) vzdálenost vyjadřuje vzdálenost každé buňky od zdroje v jednotkách nákladů. Je důležitá pro výpočet nákladů pro překonání dané vzdálenosti. Vychází z předpokladu, že různý terén pro nás představuje různé náklady na danou jednotku délky. Pohyb přes krajinu vzhledem ke způsobu využívání různých jejích oblastí (půdní kryt, kultura) je složitější než pohyb přes homogenní rovinu. Pohyb v různých prostředích vyžaduje vynaložení různého množství energie, nákladů, případně překonání různě velkých odporů. Pro modelování tohoto druhu změn se v prostředí GIS využívají analýzy nákladových vzdáleností. V tomto případě se vzdálenost počítá s využitím frikčních povrchů (Tuček, 1998).

Je využitelná při hodnocení dostupnosti rozličných lokalit s ohledem na obtížnost přechodu terénem, či konstrukci izolinií náročnosti dosáhnutí určitých lokalit. K pojmu akumulační vzdálenost se váže pojem izotropického a anizotropického povrchu (Hlásný, 2007).

Při výpočtu nákladové vzdálenosti, se vytváří nákladový povrch nebo povrch oceněných vzdáleností pro pohyb ze zdroje. V tomto případě se však vzdálenost při pohybu přes každou buňku násobí frikční hodnotou, uloženou pro každou buňku ve frikčním povrchu. Hodnoty ve výsledném nákladovém vzdálenostním povrchu budou vyjadřovat vzdálenost každé buňky od zdroje v jednotkách „nákladů“ – kaloriích, časových jednotkách, dolarech, relativních jednotkách atd., které jsou určené hodnotami ve vstupním frikčním povrchu (Tuček, 1998).

Trasování v GIS je možné na základe tzv. anizotropických povrchů, které zohledňují nejen náklady na překonání buňky s určitou hodnotou frikce danou frikčním povrchem, ale také náklady na překonání buňky v určitém směru.

Izotropický povrch je povrch u kterého se předpokládá, že možnost pohybu je ve všech směrech stejná a stejně nákladná, takže u něj nelze určit preferenční směry, ve kterých se je do určité vzdálenosti možné dostat za kratší čas, s menší vynaloženou námahou, nebo s nejnižšími náklady (Hlásný, 2007). Příkladem izotopického povrchu může být silniční síť v nížinné oblasti či plavba po jezeře kde rozdíly nákladů v různých směrech budou zanedbatelné.

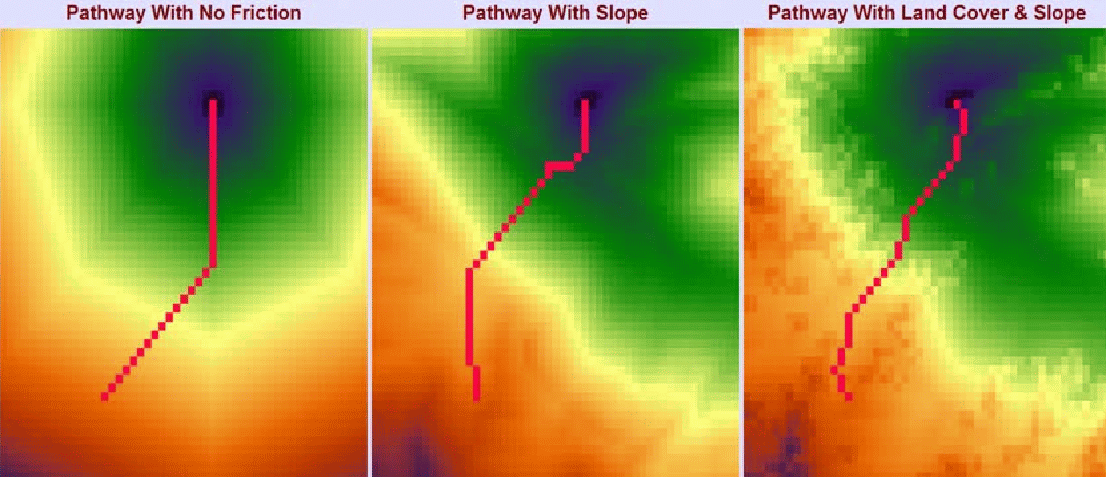
Obrázek 20: Izotropický versus anizotropický povrch - vliv sklonu a vegetačního krytu (zdroj: Stahl, 2005)

Anizotropický povrch je povrch, u kterého je možnost pohybu závislá na směru. Méně náročný terén v jistých částech území, lepší pokrytí komunikační sítí, nebo lepší spojení hromadnou dopravou, tvoří v prostoru preferenční směry, ve kterých je možné dosáhnout vzdálené lokality se stejnou námahou, jako blízké v jiném směru. (Hlásný, 2007).

Akumulační (nákladový) povrch je podobný povrchu vytvořeném na bázi Euklidiánské vzdálenosti avšak hodnoty vzdáleností od výchozího bodu nenarůstají ve všech směrech stejně, ale respektují strukturu frikčního povrchu (Hlásný, 2007).

Povrchy nákladových vzdáleností mohou být použity pro hledání cesty s nejmenšími náklady, aby se našla nejlevnější trasa ze zdroje do daného místa. Tato analýza vyžaduje další krok. Trasa se musí počítat s použitím nákladového vzdálenostního povrchu a obrazu, obsahujícího cílový objekt. Výsledný obraz znázorní trasu s nejmenšími náklady, která spojuje zdroj a cílový objekt (Tuček, 1998).

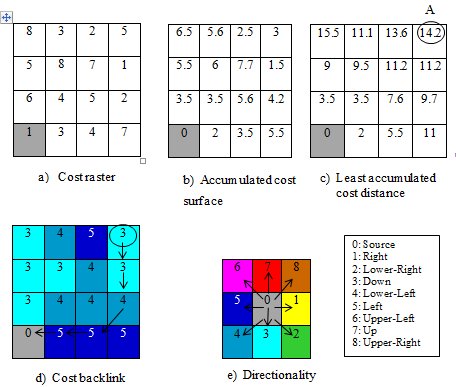
Obrázek 21: Výpočet povrchu nákladových vzdáleností (zdroj: Stahl, 2005)

Pro vytvoření akumulačního povrchu je klíčovým krokem definice frikcí, které vyjadřují prostorové rozmístění hodnot náročnosti přechodu přes jednotlivé lokality. Ty můžou relativně komplexně opisovat podmínky prostředí v kterém se pohybujeme (Hlásný, 2007).

Termín “akumulační” znamená, že jde o součet čísel, či hodnot, a to je přesně to, co nastane při vytvoření akumulačního povrchu. Hodnota každé buňky v akumulačním povrchu reprezentuje součet celkových nákladů pro její dosažení od počátečního bodu.

Frikční povrch je rastrový soubor, ve kterém hodnota uložená v každé buňce vyjadřuje úroveň obtížnosti nebo nákladovosti, potřebné pro pohyb přes ni. Takový povrch se může vytvořit např. přiřazením frikčních hodnot do obrazu využití krajiny reklasifikací (Tuček,1998). Frikční povrchy neobsahují žádné kumulativní hodnoty, ale obsahují hodnoty potřebné k vytvoření akumulačních povrchů.

Při řešení této úlohy narážíme na jistý problém – frikce na jedné lokalitě musí být vyjádřena jedním číslem, avšak náročnost přechodu může být podmíněna celou řadou faktorů. Vstupní podmiňující faktory je proto potřeba lineárně, či nelineárně transformovat do společného číselného rozsahu, takže převést originální jednotky (metry, stupně, frekvence spojení) na jednotky náročnosti přechodu, nejčastěji ve škále 0-1, 0-100, 0-255 (Hlásný, 2007).

Dále je potřeba tyto frikce syntetizovat a vytvořit anizotropický frikční povrch s absolutními hodnotami veškerých nákladů, či odporu každé buňky proti pohybu přes ni. V praxi nejčastěji využitím mapové algebry.Frikce které mohou být užitečné k anizotropickému modelování jsou např. vítr, sklon svahu, spotřeba paliva, peněžní výdaje, riziko nebezpečí nebo jiné proměnné, které potřebujeme použít. Mezi data, která shromažďuje např. armáda pro modelování možnosti pohybu patří sklon svahu, půdní pokryv, vodstvo a komunikace (Edwards, 1988).

4.5.3 Hustoty (Densities)

Jednoduchým kritériem popisu rozložení bodových objektů nebo jejich vlastností je počet bodů na jednotku plochy respektive hodnota připadající na jednotku plochy. Tento ukazatel se nazývá hustota. Jistě všichni víme, jak vypočítat hustotu zalidnění regionu, počet obyvatel regionu vydělíme rozlohou regionu. Hustotu jsme vždy počítali pro zvolené administrativní jednotky. Pomocí GIS můžeme počítat hustotu pro libovolně zvolené jednotky území. Velmi vhodné je zjišťovat hustotu za pravidelné prostorové jednotky, například za jednotlivé buňky rastru.

Hustotní povrchy tedy ukazují, kde jsou koncentrovány body nebo čáry. Jako příklad lze uvést bodovou vrstvu s informací pro každé město představující celkový počet lidí v daném městě. Chceme se dozvědět více o rozložení populace v regionu. Protože všichni lidé v každém městě nežijí v místě populace, lze vypočítáním hustoty vytvořit povrch zobrazující předpokládané rozložení populace v celé krajině.

Obrázek 22 ukazuje příklad hustoty povrchu. Když se sčítají, hodnoty populace buněk se rovnají součtu populace původní bodové vrstvy.

Obrázek 22: hustota zalidnění (zdroj: Yun et al., 2018)

Jiný příklad použití hustoty je v oblasti obchodu. Uvažujme maloobchodní prodejní řetězec, který má v určité čtvrti více obchodů. Pro každý obchod má management údaje o prodejích u zákazníků. Management předpokládá, že zákazníci upřednostňují jeden obchod před druhým na základě toho, jak daleko musí cestovat. V tomto příkladu je přirozené předpokládat, že každý zákazník si vždy vybere nejbližší obchod. Čím dále od nejbližšího obchodu, tím dále bude muset zákazník do tohoto obchodu cestovat. Ale nakupující dále mohou nakupovat i v jiných obchodech. Vedení chce studovat distribuci, kde zákazníci žijí. Z údajů o prodeji a prostorovém rozložení obchodů chce vedení vytvořit povrch zákazníků inteligentním rozložením zákazníků v celém území.

Hustota se počítá ze vstupní bodové vrstvy. Můžeme počítat hustotu bodů nebo hustotu hodnot bodů. Využitím této metody se vytvoří nová rastrová vrstva, v níž je pro každou buňku rastru vypočítána hodnota z bodů, nacházejících se v buňce a v jejím okolí (z definovaného okolí buňky - filtrovacího okna). Počet bodů, respektive suma hodnot bodů, nacházejících se v okně se vydělí jeho plochou. Oknem může být kruh nebo čtverec. Pro výpočet hustoty je důležitým parametrem velikost průzkumné oblasti. Tento parametr je volitelný uživatelem. Mapa hustoty je založena na postupném výpočtu hustoty pro každou buňku rastru zvlášť pomocí filtrovacího okénka, systém tedy postupně počítá pro každou buňku hodnoty hustoty.

Výpočet hustoty se počítá dvěma způsoby:

• jednoduchým započítáváním všech bodů (simple density),
• pomocí jádrového odhadu (kernel density).

Velikost průzkumné oblasti (filtrovacího okna) ovlivňuje vypočtenou hustotu, to ukazuje obrázek 23. Na obrázku 23a je zobrazena hustota zalidnění v České republice. Buňka rastru má hranu 1 km, hodnota buňky se počítá ze sídel vzdálených od středu buňky 10 km. Na obrázku 23b je také zobrazena hustota zalidnění v České republice. Buňka rastru má hranu 1 km, hodnota buňky se počítá ze sídel vzdálených od středu buňky 20 km.

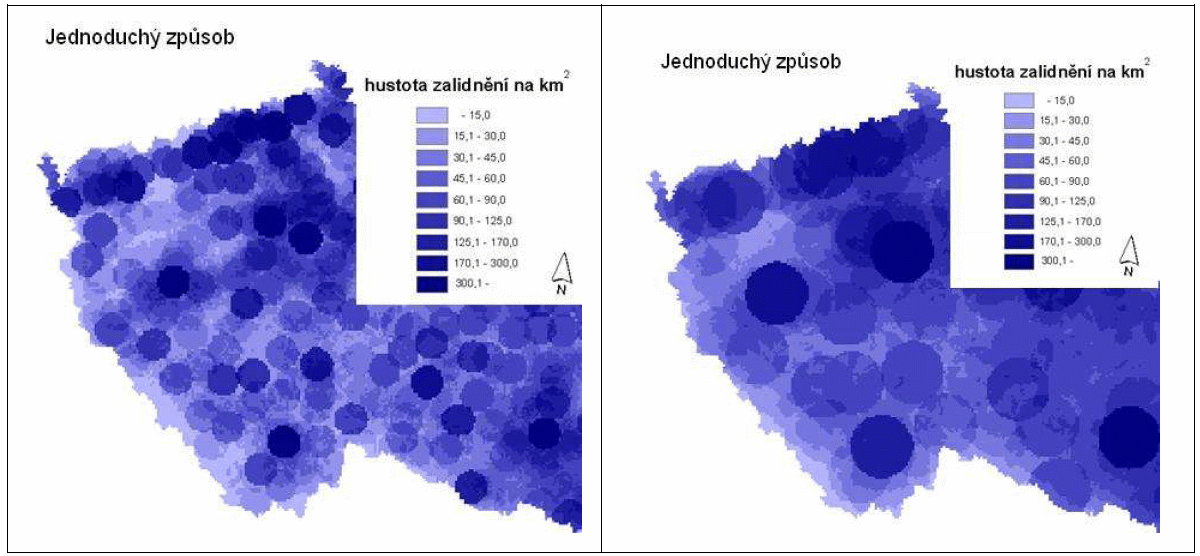
Obrázek 23: jednoduchá hustota zalidnění ČR (zdroj: Novoná, 2014)

Nevýhodou výpočtu v předešlých ukázkách je, že se do buňky započítávají všechny body z filtrovacího okna stejně, nezáleží na vzdálenosti od právě počítané buňky (respektive od středu právě počítané buňky). Tento problém pomáhá odstranit tvz. jádrové vyhlazení (kernel). Kernel je funkce, která zajišťuje, že body, které jsou blíže ke středu buňky, se započítávají více než ty, které jsou vzdálenější. Používají se různé „kernel funkce“. Představu si lze vytvořit pomocí graficky vyjádřených”kernel funkcí“.

DODĚLAT!!!!

Doporučené zdroje pro další studium

• Geospatial Analysis
• Berry, J. K.: Beyond Mapping III