Kapitola 6 Síťová analýza

Sítě jsou všude kolem nás. Silniční sítě, sítě produktovodů nebo říční sítě představují příklady sítí, které jsou často zpracovávány a analyzovány v GIS. Linie reprezentují na mapách 2 příbuzné fenomény:

• reprezentují a lokalizují skutečně lineární geografické fenomény (řeky, silnice, potrubí);
• rozdělují plochy a povrchy (hraniční linie, lomové linie).

Linie jsou popisovány páry souřadnic, mezi 2 páry souřadnic je linie rovná. Většina linií na mapě (i při velkém měřítku) vykazuje určité zakřivení. Např. silniční linie mezi 2 městy není rovná, ale zakřivuje se, často podle jiných geoprvků. Proto je zavádějící měřit přímou liniovou vzdálenost na meandrující řece. Citlivější přístup využívá měření podél středu kanálu řeky paralelně s břehy. S tím pochopitelně narůstá počet vertexů popisujících linii. Součet délky dílčích linií pak udává vzdálenost mezi 2 uzly (počátečním a koncovým). Někdy se místo měření vzdálenosti v délkových jednotkách používá cestovní čas a dopravní náklady. Pro analýzu liniového vzorku je významný také směr a spojení. Existence spojení mezi soustavou bodů, které tvoří linii, znamená, že lokace (body) na sobě nejsou nezávislé, ale jsou spojené v určitém směru. Body spojené v určitém pořadí musí zachovávat tuto posloupnost.

Interakční metody umožňují analýzu interakčních dat, tj. dat, popisujících tok mezi zdroji a cíli. Na rozdíl od jiných typů dat jsou tato data typicky vztahována k páru míst (tj. jeden zdroj a jeden cíl). Tok vyjadřuje přenos materiálu, zboží, lidí, zvířat, ale také energie nebo myšlenek mezi minimálně 2 místy. Primárním cílem analýz je porozumění prostorovým tokům a jejich modelování.

Vzhledem k rozdílnému charakteru přenášené substance se také liší prostředky, kterými se tok realizuje. Velmi často se realizuje prostřednictvím dopravních sítí. Pro popis těchto sítí a různé typy optimalizačních úloh v síti se využívá především teorie grafů. K nejběžnějším úlohám patří hledání optimální cesty.

K nejznámějším úlohám síťové analýzy patří:

• Vyhledání optimální cesty (trasy) mezi dvěma nebo více místy dopravní sítě. Trasa může být vyhledána na základě předem daných podmínek, jako např. trasa s nejkratší délkou, trasa s nejmenšími náklady apod. Nejkratší cestou rozumíme cestu, která má nejmenší délku ze všech možných cest mezi počátečním a koncovým vrcholem.
• Nalezení nejdelší či nejdražší cesty v síťovém grafu, tj. obecně nalezení cesty nejvyšší hodnoty, která může být kritickou cestou vzhledem k době trvání složitého projektu.
• Nalezení času rozšíření poruch, infekční nákazy nebo popašné zprávy v určité oblasti apod.
• Nalezení uzavřené trasy v dopravní síti - tzv. úloha obchodního cestujícího - tato úloha hledá uzavřenou cestu, která vede přes všechny vrcholy grafu a má minimální délku.
• Nalezení oblasti, jež je dostupná z jednoho místa (uzlu) sítě, tj. vyřešení dopravní obslužnosti oblasti (úloha je také známa pod názvem úloha čínského pošťáka). Praktickými aplikacemi této úlohy jsou roznáška pošty, svoz komunálního odpadu, zametání silnic apod.
• Nalezení nejspolehlivějšího spojení v síti.

V analýze interakčních dat se uplatňují 3 hlavní sady faktorů:

• prostorové vazby mezi zdroji a cíly toků,
• charakteristiky určující velikost toků ze zdrojů,
• charakteristiky určující velikost toků do cílů.

K praktickým úlohám patří hodnocení dopravní dostupnosti, lokalizační a alokační úlohy a aplikace gravitační teorie.

Z hlediska geoinformatiky je na prvním místě studium prostorových vazeb mezi zdroji a cíli. Vazby mezi zdroji a cíli mohou být vyjadřovány pomocí struktur liniových či vektorových, zpravidla bez důrazu na topografickou přesnost. Takové „nelokalizované“ linie zaznamenávají schématické spojení ze zdroje do cíle, u kterého nesledujeme trasu toku, ale pouze skutečnost existence (a velikosti, případně struktury) toku.

Vizualizace interakčních dat a tedy nejjednodušší interakční metody jsou spojeny s liniovým vzorkem, jeho reprezentací a popisem. Uplatňuje se především ve formě pohybové linie.

6.1 Popisná statistika

Kruhový liniový vzorek (modelovaný jako cyklický graf) zahrnuje smyčky (zpravidla cykly, tedy orientované uzavřené cesty) – vhodným příkladem jsou dopravní sítě. Popis tohoto lineárního vzorku se zaměřuje na topologické spojení pomocí matice dosažitelnosti. Tato matice zaznamenává přítomnost nebo nepřítomnost spojení mezi všemi páry bodů v síti.

Umožňuje porovnat různé sítě (např. srovnání počtu hran v každém uzlu sítě - nodalita - a suma těchto spojení vůči maximálnímu možnému počtu) nebo posoudit, zda je pohyb v síti mezi různými uzly volný nebo omezený.

Popis liniového vzorku

Pro popis liniového vzorku se používá řada ukazatelů:

• Gama index - hodnotí poměr zjištěného počtu hran (linií) k maximálnímu možnému počtu

\(\gamma=\frac{l}{l_{max}}=\frac{l}{3(n-2)}\),

kde \(l\) je pozorovaný počet linií (hran), \(l_{max}\) je maximální počet linií. U plošného grafu lze dokázat, že je maximální počet vždy \(3(n-2)\), kde \(n\) je počet uzlů; u neplošného (např. letecká spojení) je maximální počet roven \(n(n-1)/2\).

• Alfa index - hodnotí poměr zjištěného počtu smyček k maximálnímu možnému počtu

\(\alpha=\frac{c}{c_{max}}=\frac{c}{2n-5}\),

\(c\) je počet smyček.

Dostupnost pro celou síť může být oceněna pomocí součtu nebo průměru nodality uzlů (viz topologické míry dostupnosti).

Další ukazatelé využívají charakteristiky hran:

• minimální nebo maximální počet hran pro daný počet uzlů, který je potřebný pro vznik souvislého grafu;
• poměr počtu hran ku počtu uzlů.

Je potřebné poukázat na skutečnost, že plocha uvnitř smyčky grafu není zpravidla dle teorie grafů předmětem zájmu (vyjma výpočtu Eulerovy rovnice). Předmětem zájmu jsou uzly a hrany, nikoliv plocha mezi nimi. U grafu jsou totiž atributy připojovány k hranám, aby vznikl hodnocený graf - např. počet letadel a čas potřebný k překonání určité hrany. Uzly mohou mít připojeny např. údaj typu počet celkem přepravovaných cestujících (tedy vytížení letiště).

Náhodnost distribuce

Vedle momentového popisu liniového vzorku je možné se zabývat otázkou náhodnosti distribuce linií - tedy zda je distribuce linií náhodná, tj. zda lze pozorované uspořádání vysvětlit náhodou? Přitom se sledují rozdíly mezi pozorovanou délkou a směrem, hustotou linií, jejich zakřiveností a četností jejich délek.

Naneštěstí binomická, Poissonova i normální distribuce nejsou vhodné pro posuzování distribuce linií ze dvou důvodů. Pro ocenění délek cest, které mohou být oceněny libovolnou hodnotou a ne omezeny na celočíselné výsledky jako v případě četnosti bodů, je vhodná kontinuální hustotní funkce pravděpodobnosti.

Na distribuci pravděpodobnosti má vliv rovněž velikost studované oblasti a její tvar. Např. cesta křížící obdélníkový tvar má pravděpodobně přísně bimodální distribuci. Cesta přecházející čtverec je pravděpodobně jednomodální. V ětšina připravených analytických procedur počítá jenom přímé cesty přes oblast. Relativně malá pozornost je věnována zakřiveným liniím, jejichž délka není omezena maximální cestou přes oblast, nebo liniím, které začínají nebo končí uvnitř hranic oblasti.

Statistické analýzy stromového vzorku (příklad kanalizační sítě) se koncentruje na uspořádání (stupeň) takových sítí. Základem procedur je testování, zda pozorovaný liniový vzorek – např. 4 toky prvního stupně, 2 druhého stupně a 1 tok prvního stupně – mohl být vytvořen náhodným procesem.

Obecně se vypočítává počet alternativ, kterými může být náhodným spojovacím postupem dosaženo profilu kanálů pozorované sítě (např. kombinace 4,2,1). Počet kombinací se dělí celkovým počtem možných sítí dávajících tyto proporce. Výsledek je interpretován jako pravděpodobnost dosažení pozorovaného uspořádání kanálů náhodou.

Statistická analýza kruhového vzorku (cyklického grafu) se provádí podobně. Východiskem pro kruhový vzorek je počet uzlů a hran v pozorované síti, který má jasně kritický vliv na to, kolik topologicky rozdílných kruhů může být definováno. Statistické testy zaměřují svou pozornost na nodalitu nebo vnitřní spojitost v síti; jinými slovy jak často je každý uzel zapojen do sítě.

Pro daný počet uzlů a hran může být nodalita vyjádřena numericky rozsahem od 0 (uzel je nespojen) do \(n-1\) (\(n\) je počet uzlů), které znamená, že je každý uzel (nod) přímo spojen se všemi ostatními. Pravděpodobnost pozorované nodality je pak oceněna proti náhodnému spojení uzlů a hran.

Prvním problémem je určit náhodnou distribuci pravděpodobnosti. Na otázku, zda je uzel přímo spojen s jiným, jsou jen 2 odpovědi (nominální data). Protože je celkový počet linií v síti také konstantní, pravděpodobnost spojení uzlu s jiným uzlem se změní, když jsou již linie (hrany) využity (jde tedy o náhodný výběr bez opakování). Vhodným modelem může být hypergeometrická distribuce pravděpodobnosti. Pravděpodobnost jevu je vypočítána jako:

\(P(m,n,q)=\frac{\binom{q}{m}\binom{N-q}{n-1-m}}{\binom{N}{n-1}}\),

kde \(n,q\) jsou pozorované počty uzlů (nodů) a hran (linií), \(m\) je žádaná hodnota nodality a \(N\) celkový možný počet hran (linií).

Pozorovaná nodalita n je určena ze sumace 0 a 1 v řádku matice sousednosti (kde počítáme jen s 1 hranou mezi uzly, tj. žádné násobné hrany) při vynechání jedniček na diagonále. Hodnoty pozorované a očekávané nodality mohou být vyjádřeny v absolutních i kumulativních distribucích četnosti a maximální rozdíl mezi kumulativními součty poskytuje D test, který může být vyzkoušen pomocí Kolmogorov-Smirnovova testu významnosti.

6.2 Teorie grafů a její aplikace pro analýzu interakčních dat

Původ teorie grafů sahá do 18. století, kdy její zakladatel Leonhard Euler řešil úlohu “Sedm mostů města Královce”. Tento vyřešený matematický problém je založený na otázce, zda lze všechny mosty ve městě projít tak, aby na každý z nich ten, kdo se o to pokouší, vstoupil pouze jednou. Leonhard Euler jako první obecně prokázal, že to možné není, neboť graf odpovídající situaci nelze projít pomocí tzv. eulerovského tahu.

Teorie grafů představuje dnes již samostatně rozvinutou matematickou disciplínu, jejíž aplikace nacházíme v řadě oblastí. Široce se uplatňuje např. v operačním výzkumu, významné místo ale zaujímá v prostorové analýze, a to především interakčních dat. Postupně se však uplatňuje i pro topologický popis a analýzu areálů.

Popis teorie grafů lze nalézt v Dudorkin (1997) nebo Veverka (1989), základní pojmy a možnosti vyjádření grafů také např. v Schejbal (1993), kde je použita mírně odlišná terminologie. Protože terminologie teorie grafů není všeobecně známá ani jednotná, je potřebné uvést a vysvětlit některé pojmy.

Na prvním místě je potřebné vymezit samotný pojem graf. Za obecnou můžeme považovat definici Veverky (1989), který vymezuje graf jako matematickou strukturu modelující skutečnost, že v nějaké množině prvků existují vazby. Pro prvky se používá označení uzly, pro vazby označení hrany.

Grafem \(G\) je tedy míněna uspořádaná dvojice množin vrcholů \(V\) a hran \(E\):

\(G=(V,E)\).

Grafy jsou tedy chápány jako jistý matematický útvar, jehož základními konstruktory jsou uzly a hrany. Hrany spojují uzly a skutečnost, že hrana vstupuje nebo vystupuje z uzlu, se označuje jako incidence.

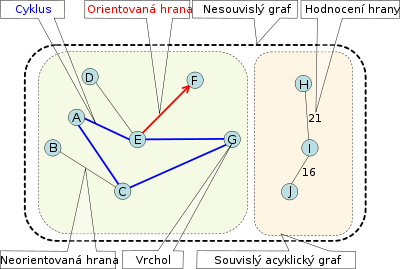
Obrázek 1: Základní pojmy teorie grafů (zdroj: https://cs.wikipedia.org/wiki/Graf_(teorie_graf%C5%AF))

Tabulka 1: Základní typologie hran a posloupnosti uzlů (zdroj: Horák, 2011)

pojem	vysvětlení, příklad
neorientovaná hrana	hrana bez orientace
orientovaná hrana	hrana s orientací (vyznačením směru)
smyčka	hrana, která inciduje s jedním uzlem
rovnoběžné hrany	hrany, které incidují se stejnými uzly
násobné hrany	rovnoběžné hrany, které jsou všechny stejně orientované nebo ani jedna z nich není orientovaná
sled mezi uzly \(u_0\) a \(u_n\)	uspořádaná posloupnost uzlů a hran mezi uzly \(u_0\) a \(u_n\)
uzavřený sled	sled, kde \(u_0=u_n\)
tah	sled, ve kterém se každá hrana vyskytuje nejvýše jednou
cesta	tah, ve kterém se každý uzel vyskytuje nejvýše jednou
kružnice	uzavřená cesta
orientované spojení	uspořádaná posloupnost uzlů a orientovaných hran mezi uzly \(u_0\) a \(u_n\), kde hrany jsou orientovány ve směru odpovídajícímu pořadí v posloupnosti
cyklus	uzavřená orientovaná cesta

Na základě typologie hran a sady hran lze vymezit základní typy grafů. Pro popis grafů a optimalizaci v grafech se používají maticové nebo relační struktury. Především jsou to:

• matice incidence - obsahuje informace o existenci spojení mezi uzly a hranami (incidence), tj. udává koncové uzly linií. Matice incidence neorientovaného grafu na obrázku 2 vypadá následnovně:

\[I=\left( \begin{array}{cccc} 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right)\]

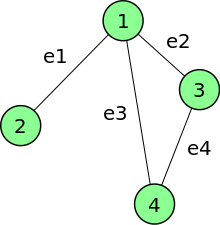
Obrázek 2: příklad neorientovaného grafu

• matice sousednosti - obsahuje počty hran mezi dvojicemi uzlů - v matematice a informatice používaný způsob reprezentace grafu. Pro konečnou množinu vrcholů grafu G, kterých je n, má podobu čtvercové matice n×n, jejíž hodnota na místě aij je celé číslo odpovídající počtu hran vedoucích z vrcholu i do vrcholu j. Prvky na diagonále tak obvykle odpovídají počtu hran vedoucích z vrcholu i do vrcholu i (takové je běžná konvence u orientovaných grafů), ovšem někdy se na diagonálu ukládá dvojnásobek této hodnoty (taková bývá konvence u neorientovaných grafů). Pro každou třídu izomorfismu grafů existuje až na prohazování řádků a sloupců právě jedna matice sousednosti a ta neodpovídá žádné jiné třídě. Příklad matice sousednosti grafu ukazuje obrázek 3.

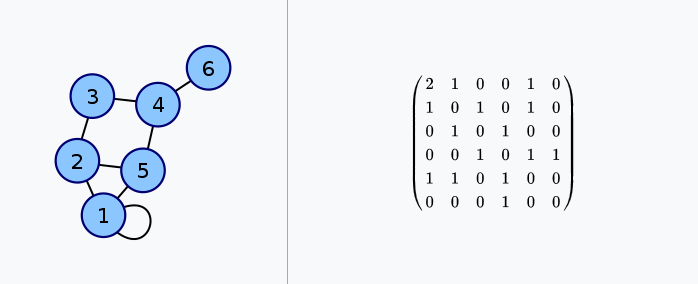
Obrázek 3: matice sousednosti vybraného grafu

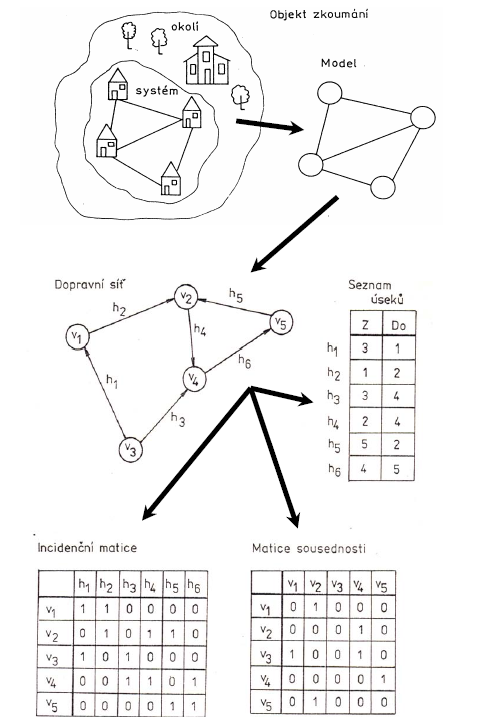
Obrázek 4: jednoduchý dopravní systém a jeho model (zdroj: Smutný, 2007)

• matice dosažitelnosti - obsahuje prvky \(b_{ij}\) , které nabývají hodnoty 1, pokud existuje sled mezi uzly \(U_i\) a \(U_j\). Matici dosažitelnosti lze odvodit z matice sousednosti pomocí Booleovského součtu a součinu. Způsob výpočtu matice dosažitelnosti pro danou síť znázorňují obrázky 5 a 6.

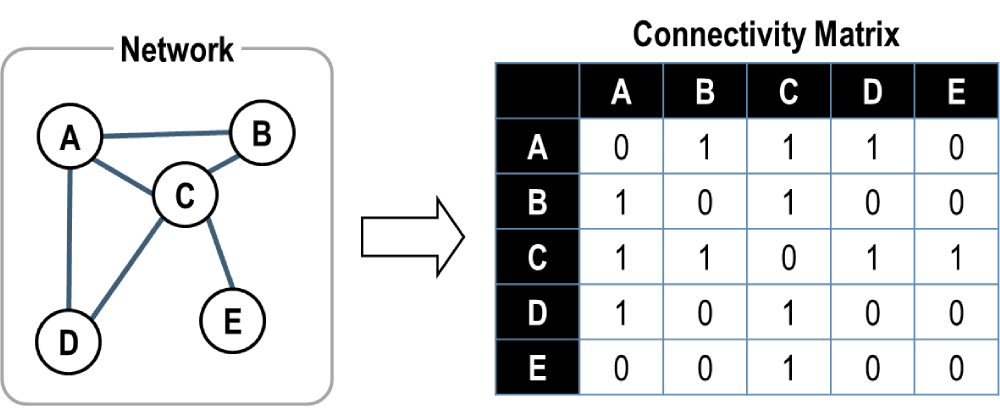
Obrázek 5: matice sousednosti vybrané sítě

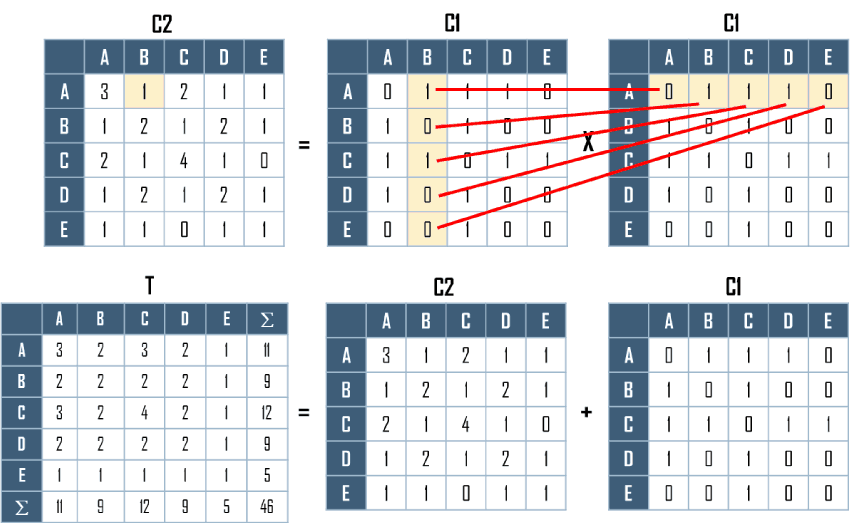
Obrázek 6: výpočet matice dostupnosti z matice sousednosti pomocí booleovských operací

Ohodnocení hran je možno zapisovat pomocí matice cen. Vzdálenostní poměry (především délku nejkratší cesty mezi \(i\) a \(j\)) lze zapisovat do distanční matice. Distanční matice je vyjádřením nepodobnosti objektů, na rozdíl od matice sousednosti, kterou můžeme chápat jako míru podobnosti. Distanční matici je možné transformovat do matice sousednosti (v obecném pojetí) pomocí jistých klasifikačních pravidel (podrobně je popisuje Tiefelsdorf 2000).

Pro praktickou implementaci teorie grafů pro síťové analýzy (např. pro optimalizaci cesty) je potřebné popsat odpor proti pohybu podél jednotlivých liniových segmentů. Ohodnocení hran, které popisuje velikost tření podle jednotlivých liniových segmentů, se zapisuje do tzv. tabulky impedance.

U grafů s mnoha cykly a rovnoběžnými hranami (např. uliční síť) je nedostatečné znát incidenci hran s uzly a impedanci segmentů (hran). Stejně důležité je vědět, zda se mohu volně pohybovat mezi jednotlivými hranami nebo zda existují nějaké bariery pro přechod (např. umístění semaforů, zákaz odbočení apod.). Musíme proto popisovat atributy párů hran nebo páry hrana-uzel. K tomu se využívá odbočovací matice (turn matrix) nebo odbočovací relace, kde se zapisuje možnost spojení (tedy odbočení) z jednoho segmentu do druhého.

Praktické úlohy řešitelné v prostředí GIS pomocí teorie grafů jsou např.:

Jaká je relativní přístupnost jednotlivých měst leteckými linkami?

Jak bude ovlivněna doprava postavením nového mostu?

Kolik alternativních cest je k dispozici při cestě z domu do práce?

K nejčastějším úlohám optimalizace v grafu patří hledání optimálních cest.

Tabulka 2: Vybrané typy grafů (zdroj: Horák, 2011)

označení	vysvětlení, příklad
orientovaný graf	obsahuje pouze orientované hrany
neorientovaný graf	obsahuje pouze neorientované hrany
smíšený graf	obsahuje orientované i neorientované hrany
prostý graf	neobsahuje násobné hrany
jednoduchý graf	prostý graf bez smyček
konečný graf	jeho množina uzlů a hran je konečná
plošný (planární) graf	je zobrazitelný v rovině bez protínání hran, hrany nemají žádné společné body (kromě uzlů), neplošný graf umožňuje realizovat např. mimoúrovňová křížení v dopr. síti
úplný graf	mezi každými 2 uzly existuje právě 1 hrana, úplný neorientovaný graf o \(n\) uzlech obsahuje \(n(n-1)/2\) neorientovaných hran
izomorfní grafy	grafy, které se liší pouze označením uzlů a hran a způsobem zakreslení (diagremem), kardinalita vztahu mezi uzly je 1:1 a stejně tak pro hrany
faktor grafu	část grafu, která má tutéž množinu uzlů
souvislý graf	mezi libovolnými 2 uzly existuje sled
silně souvislý graf	mezi libovolnými 2 uzly existuje orientovaná cesta tam i zpět
strom	souvislý graf bez kružnic
kostra grafu	faktor grafu, který je jeho stromem
cyklický graf	orientovaný graf obsahující alespoň jeden cyklus, příkladem může být dálniční nebo letecká dopravní síť
acyklické grafy	orientovaný graf bez cyklu, příkladem může být kanalizační síť
ohodnocenocený graf	Hrany nebo uzly jsou ohodnoceny. Ohodnocením se zaznamenávají kvalitativní a kvantitativní charakteristiky hran a uzlů. Používají se zpravidla kladná, reálná čísla. Prvním krokem ohodnocení prvků grafu je jejich indexace.

6.3 Hledání optimální cesty

Při hledání optimálních cest rozeznáváme úlohy:

1. nejkratší cesty (tj. cesty s nejmenším počtem hran, s nejmenším počtem přesedání),
2. nejlevnější cesty (tj. cesty s nejmenším součtem ohodnocení hran).

Někdy se nehledá pouze 1 cesta, ale více cest nejlépe splňujících dané kritérium. Každá z těchto úloh může být dále modifikována podle toho, zda se jedná o nalezení cest:

• mezi dvojicí zadaných uzlů,
• ze zadaného uzlu do všech ostatních,
• ze všech ostatních do zadaného koncového uzlu,
• pro všechny (uspořádané) dvojice uzlů.

Pro řešení těchto úloh je k dispozici řada algoritmů. Jako příklady je možné uvést tyto:

1. Dantzigův algoritmus, který umožňuje nalézt všechny nejlevnější cesty ze zadaného uzlu do všech ostatních uzlů.
2. Floydův algoritmus, který se používá pro nalezení všech nejkratších orientovaných cest mezi všemi dvojicemi uzlů (pro jednoduchý orientovaný graf).
3. Dijkstrův algoritmus, který dovoluje najít nejkratší cestu a je vhodný i pro ohodnocené grafy.
4. Hladový algoritmus, který hledá nejlevnější kostru grafu.
5. Algoritmus pro hledání Eulerovy cesty.
6. Algoritmus logického rozhodovacího stromu pro řešení úlohy obchodního cestujícího.
7. Algoritmus maximálních úspor (saving algoritmus) pro řešení úlohy obchodního cestujícího.

6.3.1 Dantzigův algoritmus

Dantzigův algoritmus umožňuje nalézt všechny nejlevnější cesty ze zadaného úhlu s do všech ostatních úhlů. Označme \(d(z)\) cenu nejlevnější cesty ze zadaného výchozího uzlu \(s\) do uzlu \(z\). Uzly, které mají stanovenou cenu nejlevnější cesty z uzlu \(s\), považujeme za prozkoumané, ostatní za neprozkoumané.

Postup:

1. krok: Pro zadaný výchozí uzel položíme \(d(s)=0\) a tím jej považujeme za prozkoumaný.Vyškrtneme všechny hrany končící v \(s\).
2. krok: Pro každý prozkoumaný uzel \(x\), který je bezprostředním předchůdcem alespoň Jednoho neprozkoumaného uzlu \(y\), vypočteme součet jeho známé minimální ceny \(d(x)\) a ceny \(c(x,y)\) hrany \((x,y)\) a nalezneme minimální z těchto součtů, tj.

\[d(z)=\min\limits_{x\in U_p} [d(x)+\limits_{y\in U_n} c(x,y)]\],

kde \(U_p\) značí množinu prozkoumaných uzlů a \(U_n\) množinu neprozkoumaných uzlů.

3. krok: Zaznamenáme vstupní hranu \((x,y)\) a z dalších úvah vyškrtneme všechny ostatní vstupní hrany do uzlu \(z\). Jestliţe byly prozkoumány všechny uzly (nebo alespoň uzly, které nás zajímají z hlediska nejlevnější cesty), je výpočet u konce, jinak následuje krok 2.

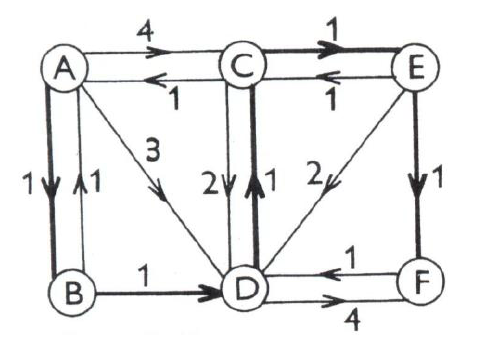
Obrázek 7: nejlevnější cesty v grafu (zdroj: Horák, 2011)

V orientovaném grafu na obrázku 7 je třeba nalézt nejlevnější cestu z uzlu A do ostatních uzlů. Výchozí údaje a výsledky výpočtu přehledně zapíšeme do tabulky 3, v jejímž sloupci jsou k příslušnému uzlu \(u\) uvedeny všechny hrany z tohoto uzlu začínající v rostoucím pořadí jejich cen. Dle popsaného algoritmu položíme \(s(A)=0\) a vyškrtneme hrany končící v uzlu A (BA,CA). Vypočteme \(d(B)=min(0+1, 0+3, 0+4)=1\). Zarámujeme hranu AB, kde toto minimum nastalo a vyškrtneme nezarámované hrany končící v B (zde takové nejsou). Vypočteme pro zkoumané uzly A, B minimum \(min(0+3, 0+4, 1+1)=2=d(D)\), zarámujeme hranu BD a vyškrtneme všechny ostatní hrany končící v uzlu D (AD, CD, ED, FD). Opakováním tohoto postupu nalézáme nejlacinější cesty z uzlu A do všech ostatních uzlů. Jejich ceny \(D(z)\) a průběh jsou snadno zjistitelné z tabulky 3. Nejlevnější cesty jsou vyznačeny v obr. 7 tučně.

Tabulka 3: výpočet nejlevnějších cest

uzel \(z\)	A	B	C	D	E	F
\(c(z,y)\)	AB(1)	BA(1)	CA(1)	DC(1)	EC(1)	FD(1)
\(c(z,y)\)	AD(3)	BD(1)	CD(2)	DF(4)	EF(1)
\(c(z,y)\)	AC(4)		CE(1)		ED(2)

6.3.2 Floydův algoritmus

Nalezení všech nejkratších orientovaných cest mezi všemi dvojicemi uzlů jednoduchého orientovaného grafu umožňuje Floydův algoritmus (Dudorkin 1997). Je použitelný i pro grafy se záporným ohodnocením hran, avšak bez cyklů záporné ceny. Ve Floydově algoritmu postupně vyčíslujeme matice \(D_0=C, D_1,…,D_n\). Prvek \(d_{ij}^{(k)}\) matice \(D_k\) (\(i=1,…,n; j=1,…,n\)) vypočteme z prvků matice \(D_{k-1}=[d_{ij}^{(k-1)}]\) dle vztahu \(d_{ij}^{(k)}=\min (d_{ij}^{(k-1)},d_{ik}^{(k-1)}+d_{kj}^{(k-1)}\), \(i=1,…,n\); j=1,…,n$; \(k=1,…,n\). Distanční matice \(D_{n}=[d_{ij}^{n}]=[d(u_{i},u_{j})]=D\), udává ceny \(d(u_i,u_j)\). Jestliže se v některé matici \(D_k\), \(k=1,…,n\), vyskytne záporný prvek na diagonále \(d_{ii}^{(k)}< 0\), potom v grafu existuje cyklus záporné délky procházející uzlem \(u_i\) a výpočet je třeba přerušit. Ve Floydově algoritmu jsou postupně počítány ceny \(d_{ij}^{(k)}\) nejlevnějších cest z \(i\)-tého uzlu do \(j\)-tého uzlu, které procházejí přes uzly \(1,2,…,k\) (kromě uzlů \(i\) a \(j\)). Při vlastním výpočtu zřejmě předcházejí \(k\)tý sloupec a \(k\)-tý řádek matice \(D_{k-1}\) beze změny do matice \(D_k\). Floydův algoritmus nalezne pouze ceny nejlevnějších cest. Pro zjištění jejich průběhu rozšíříme algoritmus o výpočet matic

\(P_{K}=[p_{ij}^{(k)}]_{n}^{n}\), \(k=1,…,n\), \(P_{0}=[p_{ij}^{(0)}]_{n}^{n}\).

Prvek \(p_{ij}^{(k)}=p_{ij}^{(k-1)}\), platí-li \(d_{ij}^{(k)}=d_{ij}^{(k-1)}\) a \(p_{ij}^{(k)}=p_{ij}^{(k-1)}\), platí-li \(d_{ij}^{(k)}=d_{ik}^{(k-1)}+d_{kj}^{(k-1)}\). Nastanou-li oba tyto případy současně, zvolíme libovolný z nich. Prvek \(p_{ij}^{(n)}\), matice \(P_n\) udává číslo uzlu bezprostředně předcházejícího uzel \(j\) na nejlevnější cestě z \(i\) do \(j\). Z matice \(P_n\) je tedy možno snadno sestavit průběh nejlevnější cesty mezi dvěma uzly. Existuje-li mezi dvěma uzly více nejlevnějších cest, je v matici \(P_n\) zaznamenána pouze jedna z nich.

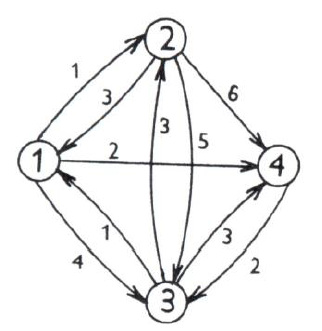
Obrázek 8: orientovaný graf (zdroj: Horák, 2011)

Mějme orientovaný graf zadaný diagramem na obrázku 8 s maticí cen

\[C=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 6 \\ 1 & 3 & 0 & 3 \\ M & M & 2 & 0 \\ \end{array}\right]\]

Z matice \(C=D_0\) postupně vypočteme matice \(D_1,…,D_4\) a \(P_0,…,P_4\) dle uvedeného postupu.

\[\begin{array}{ccc} D_0=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 6 \\ 1 & 3 & 0 & 3 \\ M & M & 2 & 0 \\ \end{array}\right], & P_0=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 2 \\ 3 & 3 & 3 & 3 \\ 4 & 4 & 4 & 4 \\ \end{array}\right] & k=0\\ \end{array}\]

\[\begin{array}{ccc} D_1=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 5 \\ 1 & 2 & 0 & 3 \\ M & M & 2 & 0 \\ \end{array}\right], & P_1=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 1 \\ 3 & 1 & 3 & 3 \\ 4 & 4 & 4 & 4 \\ \end{array}\right] & k=1\\ \end{array}\]

\[\begin{array}{ccc} D_2=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 5 \\ 1 & 2 & 0 & 3 \\ M & M & 2 & 0 \\ \end{array}\right], & P_2=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 1 \\ 3 & 1 & 3 & 3 \\ 4 & 4 & 4 & 4 \\ \end{array}\right] & k=2\\ \end{array}\]

\[\begin{array}{ccc} D_3=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 5 \\ 1 & 2 & 0 & 3 \\ 3 & 4 & 2 & 0 \\ \end{array}\right], & P_3=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 1 \\ 3 & 1 & 3 & 3 \\ 3 & 3 & 4 & 4 \\ \end{array}\right] & k=3\\ \end{array}\]

\[\begin{array}{ccc} D=D_4=\left[\begin{array}{cccc} 0 & 1 & 4 & 2 \\ 3 & 0 & 5 & 5 \\ 1 & 2 & 0 & 3 \\ 3 & 4 & 2 & 0 \\ \end{array}\right], & P=P_4=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 1 \\ 3 & 1 & 3 & 3 \\ 3 & 3 & 4 & 4 \\ \end{array}\right] & k=4\\ \end{array}\]

V maticích jsou vyznačeny řádky a sloupce, které přecházejí do následující matice beze změny a z nichž se počítají v případě matice \(D\) součty \(d_{ik}+d_{ij}\). Matice Dosahuje ceny nejlevnějších cest.

Všimněte si např. výpočtu prvku \(d_{24}^{(1)}=\min (d_{24}^{(0)}, d_{21}^{(0)}+d_{14})^{(0)}=\min (6,3+2)=5\). Protože minimum nastalo pro součet \(3+2\), bude příslušný prvek matice \(P_1\) roven \(p_{24}^{(1)}=p_{14}^{(0)}=1\). Z matice \(D\) zjišťujeme např. cenu nejlevnější cesty z uzlu 1 do uzlu 4 \(d_{14}=3\). Z matice \(P\) zjišťujeme, že uzlu 4 na nejlevnější cestě 1-4 předchází uzel 3, neboť \(p_{14}=3\). Uzlu 3 na nejlevnější cestě 1-3 předchází uzel 1, neboť \(p_{13}=1\). Tedy nejlevnější cesta z 1 do 4 vede přes uzel 3.

6.3.3 Dijskstrův algoritmus

Dijkstrův algoritmus je konečný, protože v každém průchodu jeho cyklem se do množiny navštívených uzlů přidá právě jeden uzel. Průchodů cyklem je nejvýše tolik, kolik má graf vrcholů. V grafu se nesmí vyskytnout záporné hodnoty.

Mějme graf \(G\), v němž hledáme nejkratší cestu. Řekněme, že \(V\) je množina všech vrcholů grafu \(G\) a množina \(E\) obsahuje všechny hrany grafu \(G\). Algoritmus pracuje tak, že si pro každý vrchol \(v\) z \(V\) pamatuje délku nejkratší cesty, kterou se k němu dá dostat. Označme tuto hodnotu jako \(d[v]\). Na začátku mají všechny vrcholy v hodnotu \(d[v]=\infty\), kromě počátečního vrcholu s, který má \(d[s]=0\). Nekonečno symbolizuje, že neznáme cestu k vrcholu.

Dále si algoritmus udržuje množiny \(Z\) a \(N\), kde \(Z\) obsahuje už navštívené vrcholy a \(N\) dosud nenavštívené. Algoritmus pracuje v cyklu tak dlouho, dokud N není prázdná. V každém průchodu cyklu se přidá jeden vrchol \(v_{min}\) z \(N\) do \(Z\), a to takový, který má nejmenší hodnotu d[v] ze všech vrcholů \(v\) z \(N\). Pro každý vrchol \(u\), do kterého vede hrana (označme její délku jako \(l(v_{min},u))\) z \(v_{min}\), se provede následující operace:

pokud \(d[v_{min}] + l(v_{min},u) < d[u]\), pak do \(d[u]\) přiřaď hodnotu \(d[v_{min}]+l(v_{min},u)\), jinak neprováděj nic.

Po skončení algoritmu je pro každý vrchol \(v\) z \(V\) délka jeho nejkratší cesty od počátečního vrcholu s uložena v \(d[v]\).

Uvažujme graf na obrázku 7 a hledejme cestu z uzlu 3.

\[\begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 1 & \infty \\ 2 & \infty \\ 3 & 0 \\ 4 & \infty \\ \hline \end{array}\]

\(v_{min}=3\), testujeme možnost přímého cestování z uzlu 3

\[\begin{array}{cc} \textrm{množina}\ Z\ \textrm{krok}\ 1 & \textrm{množina}\ N\ \textrm{krok}\ 1 \\ \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 3 & 0 \\ & \\ & \\ & \\ \hline \end{array} & \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 1 & \not\infty\quad 1 \\ 2 & \not\infty\quad 3 \\ 4 & \not\infty\quad 3 \\ & \\ \hline \end{array} \end{array}\]

\(v_{min}=1\), testujeme možnost přesedání v uzlu 1

\[\begin{array}{cc} \textrm{množina}\ Z\ \textrm{krok}\ 2 & \textrm{množina}\ N\ \textrm{krok}\ 2 \\ \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 3 & 0 \\ 1 & 1 \\ & \\ & \\ \hline \end{array} & \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 1 & \not 5\quad 2 \\ 4 & 3 \\ & \\ & \\ \hline \end{array} \end{array}\]

\(v_{min}=2\), testujeme možnost přesedání v uzlu 2 (žádná změna, 1+2=3, která tam už je)

\[\begin{array}{cc} \textrm{množina}\ Z\ \textrm{krok}\ 3 & \textrm{množina}\ N\ \textrm{krok}\ 3 \\ \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 3 & 0 \\ 1 & 1 \\ 2 & 2 \\ & \\ \hline \end{array} & \begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 4 & 3 \\ & \\ & \\ & \\ \hline \end{array} \end{array}\]

\(v_{min}=4\), testujeme možnost přesedání v uzlu 4, ale již není žádný neznámý uzel

Množina \(Z\) krok 4

\[\begin{array}{|c|c|} \hline \textrm{uzel}\ u & \textrm{hodnota}\ \textrm{cesty}\ d(u)\ \textrm{z uzlu}\ 3 \\ \hline 3 & 0 \\ 1 & 1 \\ 2 & 2 \\ 4 & 3 \\ \hline \end{array}\]

Pro řídké grafy je vhodné použít Dijkstrův algoritmus, jehož časová složitost se blíží \(O(V * E)\), Floydův algoritmus (časová složitost výpočtu Floydovým algoritmem je \(O(V3)\)) je naopak vhodný pro husté grafy i díky jeho jednoduché implementaci. Podstatný rozdíl mezi algoritmy spočívá ve schopnosti Floydova algoritmu provést výpočet i nad grafem se zápornými vahami hran (ale bez záporných cyklů), kdežto u Dijkstrova algoritmu v některých případech nikoliv.

6.3.4 Základní algoritmus pro nalezení nejlevnější kostry

Mějme dán úplný neorientovaný graf \(G=(U,H,R)\) a matici cen \(C\geq 0\). Máme nalézt takovou jeho kostru \(G_1=(U,H_1,R_1)\), která je nejlevnější, tj. jejíž součet ohodnocení všech jejich hran je minimální ze všech možných koster. Metoda k nalezení této nejlevnější kostry je poměrně jednoduchá a popíšeme ji slovně (Horák, 2011): 1. krok: Zvolíme libovolný uzel grafu \(G\) a spojíme jej s cenově „nejbližším“ uzlem. 2. krok: Nalezneme dosud „nepřipojený“ uzel, který je cenově „nejblíže“ k některému z již „připojených“ uzlů a spojíme jej s ním. 2.krok opakujeme tak dlouho, dokud nebudou propojeny všechny uzly.

6.3.5 Hladový algoritmus

Nejlevnější kostru je možno také nalézt tzv. hladovým algoritmem (Horák, 2011). Seřadíme hrany grafu vzestupně dle jejich cen. V tomto pořadí je postupně vybíráme, přičemž pro každou vybíranou hranu kontrolujeme, zda netvoří s již vybranými hranami kružnici. Tvoří.li kruţnici, zamítneme ji;jinak ji zařadíme do seznamu vybraných hran. Postup opakujeme tak dlouho, dokud nezískáme kostru grafu. Lze ukázat, že je nejlevnější. V příkladu na obrázku 9 zařazujeme hrany v pořadí 5-8, 5-6, 3-6, 4-5, 1-2, 7-8-, 8-9-, 1-4. Přidání dalších hran by již vedlo ke vzniku kružnice.

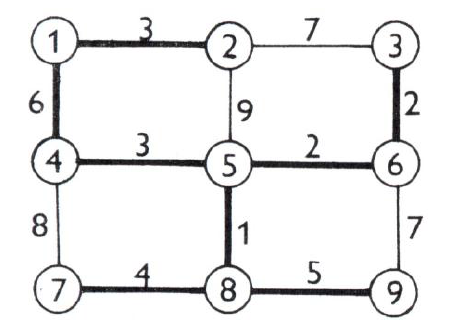
Obrázek 9: nejlevnější kostra grafu (zdroj: Horák, 2011)

6.4 Úloha obchodního cestujícího

Uvažujme úplnou dopravní síť se střediskem 0 a ostatními uzly 1,2,…,n. Nechť \(c_w\) je délka úseku \((u,v)\). Pak můžeme úlohu obchodního cestujícího na této síti formulovat následovně:

Minimalizujte

\(M=\sum\limits_{u=1}^{n}\sum\limits_{j=1}^{n}c_{uw}x_{uw}\)

za podmínek

\(\sum\limits_{v=1}^{n}x_{uv}=1\qquad u=0,1,\dots,n\)

\(\sum\limits_{u=1}^{n}x_{uv}=1\qquad v=0,1,\dots,n\)

\[\sum\limits_{u\in S}\sum\limits_{v\in S}x_{uv}\leq |S|-1\qquad S\subset\{1,2,\dots,n\}\],

kde symbolem \(|S|\) označujeme počet prvků množiny \(S\), \(x_{uv}\in\{0,1\}, u=0,1,\dots,n; v=0,1,\dots,n\).

V tomto modelu vyjadřuje výraz \(M\) celkovou délku projetých úseků, první podmínka vyjadřuje, že do každého uzlu sítě vozidlo přijede práv jednou, podmínky druhá vyjadřuje, že z každého uzlu sítě vozidlo odjede právě jednou a poslední podmínky zabezpečuje, že použité úseky budou tvořit jedinou okružní jízdu.

Pro symetrickou úlohu obchodního cestujícího, jež odpovídá úloze obchodního cestujícího v neorientované dopravní síti, kde je matice {cuv} ohodnocení úseků symetrická, můžeme použít jednoduššího modelu s přibližně polovičním počtem proměnných.

Dnes existuje mnoho klasických i nových metod použitelných k řešení problému nalezení optimálního řešení „Úlohy obchodního cestujícího“. Značný počet těchto metod je použitelný pouze u sítí s malým množstvím uzlů (cca 50 až 100). Snad nejstarší metodou je Croesova metoda (Smutný, 2007).

U této metody se vychází z nějakého počátečního řešení v podobě množiny použitých úseků dané sítě. Ohodnocení úseků dopravní sítě jsou transformována tak, aby zůstalo zachováno uspořádání všech přípustných řešení vzhledem k hodnotám účelové funkce a aby použité úseky byly ohodnoceny nulovými hodnotami. Nepoužité úseku jsou ohodnoceny nezápornými nebo zápornými reálnými čísly, vyjadřujícími o jakou hodnotu by se účelová funkce v prvním případě zvýšila, ve druhém případě snížila, pokud by se podařilo zavést příslušný úsek.

Protože množinu použitých úseků je v této metodě možné měnit jen tak, aby úseky tvořily jednu jízdu procházející právě jednou každým uzlem, vynutí si obecně zavedení úseku se záporným ohodnocením další úseky, které již nemusí mít záporné ohodnocení. Hodnota účelové funkce získaného řešení se bude potom od hodnoty předchozího řešení lišit o součet ohodnocení nových úseků.

Princip metody je tedy ve vybrání takového úseku se záporným ohodnocením, jehož zavedením do řešení a provedením všech nutných změn se hodnota účelové funkce nového řešení sníží. V dalším kroku jsou ohodnocení použitých úseků opět transformována a celý postup je opakován, dokud není zjištěno, že zavedení žádného úseku se záporným ohodnocením současné řešení nevylepší.

Další metodou dříve velmi používanou pro řešení „Úlohy obchodního cestujícího“ je dynamické programování. Metoda spočívá v postupném výpočtu nejkratších cest spojujících vybrané uzly a procházejících uzly specifikované množiny. Výpočet nejkratších cest je prováděn nejprve pro množiny mohutnosti 1, pak 2 atd., dokud neobdržíme nejkratší okružní jízdu, začínající a končící ve středisku a procházející všemi uzly dané sítě. Další z efektivních metod jsou např. aplikace známé metody větví a hranic, aplikace simplexové metoda apod.

Jak bylo již dříve uvedeno, výše uvedené metody jsou vhodné pro sítě s malým počtem uzlů. V praxi často stojíme před úkolem optimalizovat dopravní sítě s velkým počtem uzlů. Často se proto přechází na metody, kde nalezené řešení nebude zcela optimální, ale hodnoty účelové funkce se k optimálnímu řešení blíží. Opět podotkněme, že existuje celá řada přístupných metod, velmi stručně vzpomeňme např. algoritmus postupného zvětšování, nejvýhodnějšího souseda, nejvýhodnějšího úseku, frekvenční algoritmus postupného zvětšování apod.

6.4.1 Metoda nejbližšího souseda

Předpokládejme, že \(i_1,i_2,\dots,i_k\) jsou uzly zařazené do trasy, \(W=v-[i_1,i_2,\dots,i_k]\) jsou uzly nezařazené do trasy, \(V\) jsou uzly dopravní sítě, \(k\) je krok algoritmu a \(i\) naposledy zařazený uzel. Výpočet je realizován takto:

1. Položíme \(i=i_1=1,\ W=[2,3,\dots,n]\) a \(k=1\), pak přejdeme na bod 2.
2. Je-li \(k<n\), je možné nalézt \(c_{ij}=\min\limits_{q\in W}\{c_{iq}\}\), položíme postupně \(k=k+1,\ i=i_k=j\), \(W=W-\{j\}\) a opakujeme bod 2. Je-li \(k=n\), položíme \(i_{n+1}=1\) a ukončíme výpočet s tím, že řešení je dáno posloupností uzlů \(i_1,i_2,\dots,i_n,i_{n+1}\).

6.5 Způsoby hodnocení dopravní dostupnosti

Jedním z nástrojů zkoumání prostorové interakce mezi zdroji a cíli a popisování prostorových vazeb je i průzkum a popis dopravní dostupnosti. Pojem dostupnosti geografických objektů byl rozpracován již v 50. a 60.letech. K popisu dostupnosti se používají různé míry dostupnosti, významně se uplatňuje teorie grafů.

Dostupnost je chápána jako určitý ukazatel, který na základě přístupnosti nebo dosažitelnosti daného objektu k ostatním objektům určuje jeho postavení v rámci dané prostorové struktury (Kusendová 1996). Někteří autoři používají pojem akcesibilita (Maryáš et al. 1995). Dostupnost je chápána jako geografický pojem, geografická charakteristika objektu. Stanovuje se na základě vzdálenostních charakteristik v rámci bodové nebo liniové struktury.

Míry dostupnosti dovolují popisovat dostupnost geografických objektů a uplatňují se především v socioekonomické geografii.Míry dostupnosti můžeme podle použité metriky (zjednodušeně podle použitých jednotek) dělit na:

1. metrické,
2. časové,
3. topologické,
4. cenové (nákladové),
5. ostatní.

Příkladem posledně jmenované míry je např. fyziologický index únavnosti, který zahrnuje informaci o délce pěších cest k dopravnímu prostředku a hodnotí i jakost přepravy - její únavnost (Hůrský 1969). Vedle základních měr dostupnosti se uplatňují i vážené míry dostupnosti.

Dostupnost lze dělit i podle jiných hledisek, např. podle dopravního prostředku, pro který je zjišťován. Pak bychom dělili dostupnost na určenou podle provozně organizačního hlediska pro hromadnou a individuální dopravu, podle provozně technického hlediska na veřejnou a neveřejnou dopravu. Ze všech kombinací má smysl sledovat především neveřejnou individuální dopravu a veřejnou hromadnou dopravu. K termínu „dostupnost“ má relativně blízko pojem dopravní obslužnost, která je vztahována k veřejné hromadné dopravě.

6.5.1 Metrické míry

Metrické míry používají vzdálenosti měřené jako přímé (vzdušné, euklidovské) a nebo cestní (po komunikaci).

Míra přímé dostupnosti (euklidovské)

U této míry dostupnosti není potřebná konstrukce grafu, využívají se pouze euklidovské (vzdušné) vzdálenosti, takže ji lze snadno vypočítat ze souřadnic zkoumaných míst. Nejlepší dostupnost má místo s nejmenší hodnotou přímé euklidovské vzdálenosti, což odpovídá těžišti cílových objektů.

\(D_{i}^{P}=\sum \limits_{j} d_{ij}^{v}\),

kde \(D_{i}^{P}\) je míra přímé dostupnosti v místě \(i\), \(d_{ij}^{v}\) euklidovská vzdálenost mezi místy \(i\) a \(j\), \(j\) je index cíle.

Míra cestní dostupnosti

Míra cestní dostupnosti používá výpočet vzdálenosti po trase přesunu, tedy vlastně délky cest v grafu. Cestní vzdálenost se stanovuje zpravidla na základě určitého modelu dopravní sítě, jehož přesnost je závislá na měřítku a úrovni generalizace. Často se odvozuje v prostředí GIS pomocí síťových funkcí typu nejkratší cesta. Proto je výpočet nejkratší vzdálenosti mezi jednotlivými místy nutně zatížen jistou chybou. Proto je vhodnější používání označení „cestní vzdálenost“ na místo „skutečná vzdálenost“.

Nejlepší cestní dostupnost má místo s nejmenší hodnotou ukazatele:

\(D_{i}^{C}=\sum \limits_{j} d_{ij}^{c}\),

kde \(D_{i}^{C}\) je míra cestní dostupnosti v místě \(i\), \(d_{ij}^{c}\) délka nejkratší cesty z místa \(i\) do místa \(j\), \(j\) je index cíle.

Při řešení nejkratší cesty se používají především techniky lineárního programování (viz hledání optimální cesty).

Vedle základních údajů typu přímá vzdálenost a cestní vzdálenost se používají i další ukazatele typu rozvoj čáry (poměr mezi cestní a přímou vzdáleností) či koeficient okliky (o kolik % je cestní vzdálenost větší neţ přímá vzdálenost) Teoreticky by bylo moţné vyčlenit metody přímé sférické zaloţené na použití sférické geometrie, avšak hodnocení dostupnosti velkých regionů, kde se již uplatní zakřivení Země, se prakticky neprovádí.

6.5.2 Časové míry dostupnosti

Do skupiny časových měr řadíme především časovou dostupnost. Vyjadřuje celkovou dobu cestování ze zkoumaného zdroje do všech cílů hvězdicovým způsobem. Nejlepší časovou dostupnost má potom uzel (místo) s nejmenší hodnotou časové dostupnosti.

\(D_{i}^{t}=\sum \limits_{j} t_{ij}^{c}\),

kde \(D_{i}^{t}\) je míra časové dostupnosti v místě \(i\), \(d_{ij}^{t}\) doba nejkratšího přesunu z místa \(i\) do místa \(j\), \(j\) je index cíle.

Zde se analogicky k cestní dostupnosti sčítají cestovní časy mezi uzly \(i\) a \(j\). Cestovní časy můžeme chápat jako časovou vzdálenost (uvaţují se potom pouze doby samostatného nejrychlejšího přesunu) nebo jako časovou ztrátu. Ta má smysl v případě využívání veřejné hromadné dopravy, kdy do doby cestování zahrnujeme i dobu čekání na odjezd dopravního prostředku.

6.5.3 Topologické míry dostupnosti

Topologické míry dostupnosti využívají teorie grafů.

Přímá topologická dostupnost

Vyjadřuje celkový počet sousedních uzlů v grafu. Místo (uzel) s nejvyšším počtem sousedů má nejlepší přímou topologickou dostupnost.

\(D_{i}^{U}=\sum \limits_{j} I_{ij}\),

kde \(D_{i}^{U}\) je míra přímé topologické dostupnosti v místě \(i\), \(I_{ij}\) indikátor sousedství vzhledem k uzlu (nabývá hodnoty 1 v případě existence sousedství, jinak 0, lze získat z matice sousednosti), \(j\) je index cíle.

Nepřímá topologická dostupnost

Vzdálenosti mezi uzly jsou vyjadřovány počtem hran na nejkratší cestě mezi nimi. Nejlepší nepřímou topologickou dostupnost bude mít uzel s nejmenší hodnotou ukazatele, podle teorie grafů se jedná o střed grafu, tedy o uzel s minimální excentricitou.

\(D_{i}^{H}=\sum \limits_{j} d_{ij}^{h}\),

kde \(D_{i}^{U}\) je míra nepřímé topologické dostupnosti v místě \(i\), \(d_{ij}^{h}\) počet hran na nejkratší cestě mezi místy \(i\) a \(j\), \(j\) je index cíle.

6.5.4 Cenové míry dostupnosti

Cenové míry dostupnosti jsou založeny na ceně dopravy, v případě individuální dopravy na nákladech dopravy.

U veřejné hromadné dopravy se sleduje cena placená za přepravu mezi jednotlivými místy (zpravidla základní jízdné bez různých slev). V některých případech se vybírá dopravní prostředek, v jiných měřeních se povoluje přestupovat mezi prostředky. Více variant nabízí sledování individuální dopravy, kde vedle výběru dopravního prostředku se může sledovat jen spotřeba pohonné látky (přepočtená na cenu) nebo se může zahrnout i amortizace vozidla.

\(D_{i}^{F}=\sum \limits_{j} c_{ij}\),

kde \(D_{i}^{F}\) je míra cenové dostupnosti v místě \(i\), \(c_{ij}\) cena přepravy z místa \(i\) do \(j\), \(j\) je index cíle.

6.5.5 Vážené míry dostupnosti

Jednoduché míry dostupnosti povaţují všechny geografické objekty, které představují zdroje (resp. cíle) toků za rovnocenné a přidělují jim stejnou váhu. Proto prvním rozšířením uvedených základních modelů je zahrnutí atraktivity center, tedy cíle cestování.

Příkladem může být vážená časová dostupnost vyjádřená

\(D_{i}^{tv}=\frac{\sum \limits_j t_{ij}F_{j}}{\sum \limits_j F_{j}}\),

kde \(D_{i}^{tv}\) je míra dostupnosti v místě \(i\), \(F_{j}\) atraktivita cíle \(j\). Podobně i další míry dostupnosti (např. cestní dostupnost) je možné vážit.

6.6 Lokalizační a alokační úlohy

Se studiem interakčních dat a jejich modelováním jsou spojovány často používané lokalizační a alokační úlohy.

Lokalizační úlohy řeší problém optimálního umístění zařízení či objektu. Umístění je optimalizováno z hlediska optimalizačního kritéria, které závisí na charakteru úlohy a funkci zařízení. Kritérium může zahrnovat náklady na umístění zařízení (cena pozemku, výstavby a vybavení), tak především maximalizaci poskytovaných funkcí. Alokační úlohy se zaměřují na problém optimálního zásobování. Existující zařízení je třeba optimálně „vybavit“, aby dobře plnila své funkce.

Je zřejmé, že oba typy úloh spolu úzce souvisí. Optimálně lze ovšem přiřazovat i úkoly jednotlivým pracovištím apod. - takové úlohy někteří autoři (především z oblasti operačního výzkumu) označují jako přiřazovací úlohy. Lokalizační úlohy jsou často vyuţívány socioekonomickými geografy, dříve se však zabývaly především rozmístěním výrobních kapacit ve vazbě na trh a dopravní náklady. Klasickým modelem v tomto směru je Thünenův model rozmístění jednotlivých druhů zemědělské produkce od centrálně situovaného trhu. V současnosti se lokalizační a alokační úlohy vyuţívají při optimalizaci rozmísťování nových administrativních, komerčních či obslužných objektů a optimalizaci jejich vybavení.

Příklady lokalizačních úloh: umístění optimálního centra pro síť zákazníků, úložiště jaderných odpadů, střediska údržby pro několik závodů apod.

Příklady alokačního problému: distribuce zboží do sítě prodejen v adekvátním množství vzhledem k rozmístění potenciálních zákazníků, přiřazení žáků do škol apod.

Lokalizační úloha se zabývá volbou umístění zařízení, zpravidla ve vztahu k rozmístění zákazníků.

Pojmem zařízení budeme označovat objekty libovolného druhu, která poskytují jisté služby a jejichž umístění či vybavení závisí na lidské aktivitě. V typických aplikacích se jedná o obchody, zdravotnická zařízení, hasičské stanice, školy, úřady, firmy, informační centra, skládky, ale i např. krmná zařízení či útočiště pro zvířata, přírodní rezervace, zóny klidu apod.

Jako zákazníky označíme spotřebitele nebo uživatele služeb poskytovaných zařízeními, jejichž umístění či vybavení je optimalizováno. Mohou to být nakupující dojíždějící do obchodů, děti dojíždějící do škol, občané k úřadům, zaměstnanci do zaměstnání, pacienti k lékařům, zvířata cestující za potravou apod. Mohou to být také organizace odebírající zboží z velkoskladu, dopravní prostředky využívající čerpací stanice, výrobní stroje odebírající elektřinu z transformátoru, odpady atd. V operačním výzkumu se často řeší úlohy, kde optimalizujeme umístění dalšího zařízení pouze v závislosti na existujících zařízeních.

Pro řešení lokalizačních úloh je nutno zváţit podmínky prováděné analýzy. Především je důležité, zda:

• můžeme umísťovat 1 nebo více nových zařízení,
• se může nebo nemůže měnit počet a velikost zařízení (dynamické versus statické řešení),
• zařízení jsou reprezentovaná bodem nebo areálem,
• umístění nových zařízení závisí nebo nezávisí na existujících,
• množina přípustných umístění je spojitá (nové zařízení lze umístit kamkoliv) nebo diskrétní (např. výběr z nabídky pozemků). Druhá varianta se lépe řeší s vyuţitím teorie grafů a heuristických postupů.

Při řešení lokalizačních a alokačních úloh se uplatňuje matematické programování (lineární i nelineární), optimalizace na grafech a heuristické postupy. Některé metody neobsahují podmínku optimalizace vzdálenosti, protoţe postačuje pouze splnění vzdálenostního limitu (např. pro optimalizaci rozmístění zařízení naléhavé potřeby na území města při splnění limitu časové dostupnosti).

Základní krokem je volba optimalizačního kritéria. Obecně jím může být například:

• maximalizace zisku (tj. rozdílu mezi příjmy plynoucími z poskytování služeb zákazníkům a náklady na výstavbu zařízení a jejich provoz),
• maximalizace objemu toků (co nejvyšší objem poskytovaných služeb),
• minimalizace délky toků (časové, metrické či nákladové) při dosaţení limitního (resp. nadlimitního) objemu toků či splnění jiného limitu (např. doba cestování nesmí překročit jistý limit),
• maximalizace efektu pro zákazníka,
• minimalizace nákladů pro zákazníka.

Klasické metody jsou deterministické a předpokládají, že toky směřují k nejbližšímu cíli. Tímto způsobem vznikají jasně vymezené a nepřekrývající se spádové oblasti kolem jednotlivých zařízení. To je vhodné pro lokalizaci administrativních zařízení nebo v optimalizaci umístění zařízení naléhavé potřeby.

Ve skutečnosti je chování toků (inicializované zákazníky) málokdy deterministické, ale spíše neurčité a je vhodné ho modelovat pomocí pravděpodobnostních a behaviorálních modelů. U nich pak vzdálenost vystupuje sice jako důležitý faktor, ale ne jako striktní omezení. Připouštějí takové rozloţení toků, kde největší tok směřuje k nejbližšímu cíli, ale i vzdálenější zařízení jsou cílem jistého menšího toku z daného místa.

V některých případech může být výhodné pouţití etapového postupu při určování cílů, který odpovídá praktické zkušenosti, kdy v případě malých rozdílů mezi vzdálenostmi/náklady již tyto nehrají při výběru žádnou roli. Thill a Horowitz (1997) popisují dvouetapový model s tím, že v první etapě se vybírá jistá množina kandidátů podle cestovní vzdálenosti a ceny dopravy, a teprve ve druhé etapě se určují vhodné alternativy z této skupiny kandidátů.

Optimalizačních kritérií, a tedy i prostorových interakčních modelů, může být celá řada. Uvedeme 3 základní kritéria:

• minimalizace délky toků - jednodušší model používá jako kritérium minimalizaci procestovaných vzdáleností v systému za předpokladu cestování zákazníků k nejbližšímu zařízení. Umísťuje se \(p\) zařízení do \(n\) uzlů (diskrétní úloha).

Kritéria:

\(\min \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} a_{i}I_{ij}d_{ij}\qquad\sum\limits_{j=1}^{n} I_{ij}=1\qquad \sum\limits_{j=1}^{n} I_{ij}\geq 1\),

kde \(d_{ij}\) je cena cestování z \(i\) do \(j\) (např. vzdálenost), \(a_i\) je velikost požadavku na službu od zákazníka \(i\) (zjednodušeně objem požadovaných služeb v místě \(i\)) - např. počet obyvatel, velikost určité části populace, cena majetku; \(I_{ij}\) je indikátor, který nabývá hodnoty 1 pokud je v místě \(j\) poskytována služba \(i\) nebo hodnoty 0, pokud tomu tak není.

Druhá podmínka (suma \(I_{ij}\)) musí být splněna pro všechna \(i = 1...n\), protože každý požadavek je vyřizován právě jedním zařízením.

Není omezení kapacity cíle.

Jednoduchý model předpokládá lineární závislost celkových nákladů na vzdálenosti nového zařízení od zákazníků (délky toků). Lineární závislost je samozřejmě nejsnáze řešitelná (např. metodou nejmenších čtverců). Obecněji lze uvažovat o náhradě dij za funkci \(g(dij)\), která může zahrnovat jak lineární tak nelineární modely (musí však být k dispozici vhodné řešení matematické úlohy).

Pro \(p=1\) se úloha označuje jako Weberův problém, pro obecný počet zařízení \(p\) jako \(p\)-mediánové umístění. Praktická řešení pro umístění jednoho i p zařízení uvádí např. Dudorkin (1997), který popisuje algoritmizaci úloh pro euklidovskou vzdálenost, manhatonskou vzdálenost (rektilineární) i pro kvadrát euklidovské vzdálenosti, doporučovaný např. pro optimalizaci umístění hasičských stanic. Pro jednoduché přiřazovací úlohy se doporučuje tzv. maďarská metoda.

Řešení těchto úloh je k dispozici jak pro kontinuální tak pro diskrétní moţnost lokalizace, pro diskrétní je ovšem algoritmizace obtíţná vzhledem k rozsahu reálných úloh a tak se často používají různé heuristické postupy.

Rozšíření základního modelu dovoluje zohlednit náklady umístění zařízení v daném místě, kapacitní omezení v daném místě (např. kapacita nemocnice či počet pracovních míst), omezení na maximální délku toku (maximální vzdálenost, kterou je zákazník ochoten překonat, či např. cena za dopravu, kterou je zaměstnanec ochoten při dojíždění do zaměstnání zaplatit). S rozšiřováním základního modelu dochází často k automatickému uvolnění původního požadavku na cestování do nejbližšího místa.

• minimaxové řešení - kritériem je minimalizace vzdálenosti toků. Praktické řešení úlohy pro 1 zařízení poskytuje např. Elzingův algoritmus.

• maximalizace pokrytí - kritériem je maximalizace počtu zákazaníků při splnění limitu, kladeného na tok (čas, vzdálenost nebo náklady na nižší než stanovený limit)

\(\min\sum\limits_{i=1}^{n} a_{i}I_{i}(h)\qquad\quad\sum\limits_{j=1}^{n}j_{ij}\geq 1\),

kde \(d_{ij}\) je cena cestování z \(i\) do \(j\), \(a_i\) je velikost požadavku na službu od zákazníka \(i\), \(I_i(h)\) je indikátor, který nabývá hodnoty 1 pokud místo \(i\) je za limitní vzdáleností \(h\) od každého zařízení (tedy pokud není zákazník “pokryt”) nebo hodnoty 0, pokud tomu tak není; \(J_{ij}\) je indikátor nabývající hodnoty 1, pokud není zařízením \(j\) poskytována služba pro zákazníka \(i\) nebo hodnoty 0, pokud zařízení tuto službu poskytuje, platí pro všechna \(d_{ij}\leq h\).

První podmínka minimalizuje množství nepokrytých zákazníků. Poslední uvedený model má zajímavé vlastnosti. Model je obecnější - např. pro velké \(h\) přechází v minimaxové řešení. Výhodou je rovněž možnost sledování chování v případě změny \(p\) a zjišťování např. kolika zařízení (\(p\)) je potřeba pro dosažení určité úrovně pokrytí.

Vzhledem k výpočetní náročnosti se opět často uplatňují heuristické postupy.

6.6.1 Rozšíření základních modelů

Tyto základní modely je možné upravit - např. vyloučení obsloužených zákazníků a využití vzdálenostního hendikepu pro eliminaci vlivu zanedbatelných rozdílů ve vzdálenosti.

Další rozšíření modelu zahrnují např. hierarchické lokalizačně-alokační modely, které dovolují umístit více zařízení, které však neposkytují služby stejné úrovně. Příkladem mohou být zdravotnická zařízení, z nichţ některé jsou jen se základním vybavením a jiná mají i specializovaná pracoviště. Některé modely zohledňují i různou atraktivitu zařízení, vycházející např. z jejich velikosti (analogie gravitačních modelů).

Konečně se uplatňují i multikriteriální modely, kde je současně pro optimalizaci použito více kritérií, problémy jsou pak především v realizaci řešení. V případě dynamického řešení se optimalizace rozšiřuje a používá se sumace vah za zkoumané časové období. Z konstrukce modelů vyplývají minimální poţadavky na vstupní data a specifikace vztahů.

V minimální variantě musí být známo:

• optimalizační kritérium,
• umístění zákazníků,
• umístění stávajících zařízení (alespoň pro statické řešení),
• způsob realizace toků (např. dopravní spojení, elektrické vedení),
• vyjadřování vzdálenosti (např. měrné náklady na realizaci spojení v závislosti na vzdálenosti).

Diskrétní úlohy jsou zpravidla simulovány pomocí matematických grafů. V prostředí GIS se však setkáváme i s jinými typy úloh. Některé lokalizační problémy nejsou orientované na grafy.

Např. lidské nebo přírodní toky se mohou vyskytovat mezi určitými body nebo mezi bodovými a liniovými prvky (např. plošný tok znečištění přes plochu k řece, kde končí). Takový problém může vyžadovat speciální hledání cesty přes povrch s různými podmínkami, která jsou reprezentována polygony nebo buňkami měřítky nebo který můţe zahrnovat tvorbu virtuálních spojení mezi body. Předpověď objemů přepravovaných vzduchem (znečistění vzduchu) uvnitř města byla dříve často modelována gravitačním modelem, vyžadujícím výpočet velikosti uzlů a jejich vzdálenost v mřížce.

Na závěr je potřebné upozornit na některé specifické problémy při praktických aplikacích.

Především je nezbytné zohlednit tzv. hraniční problém. Modely mohou být prakticky omezené hranicemi sledovaného území, které se nemusí krýt s funkčním vymezením pomocí optimalizačního kritéria (tedy se spádovou oblastí). Fyzické omezení modelu může narušovat proces optimalizace i vlastní využívání modelu.

Řada modelů využívá pro informaci o zákaznících informace o obyvatelstvu s trvalým bydlištěm v dané zóně (a zjišťují model závislosti určitého podílu zákazníků z celkového množství obyvatelstva) v závislosti na vzdálenosti od služby). Reálná situace je ovšem komplikována mobilitou zákazníků (dojíždění za prací apod.) a rovněž i změnami v demografické situaci (časový vývoj v populaci).

Na druhou stranu je třeba upozornit, že nemá smysl vytvářet zbytečně komplexní modely. Do praktického rozhodování stejně vstupují další hlediska a požadavky, které nelze nebo není efektivní zahrnout do prostorové optimalizace. Málokdy jsou modelová řešení použita ke skutečné optimalizaci, zpravidla jsou použita pro podporu rozhodování při srovnávání variant či průzkumu situace. Pro jejich správnou interpretaci je pak nezbytná jasná koncepce a konzistence modelu.

6.7 Úloha okružních jízd (Vehicle Routing Problem)

Úloha okružních jízd (Vehicle Routing Problem) bývá označována jako problém vícenásobného obchodního cestujícího (Multiple Travelling Salesman Problem). Již uplynulo více než 50 let od chvíle, kdy Dantzig a Ramser v roce 1959 představili problém okružních jízd ve své práci nazvané The Truck Dispatching Problem. Popsali ho na skutečném příkladu týkajícím se dodávky benzínu do čerpacích stanic a navrhli první matematickou formulaci a algoritmický přístup k problému. O několik let později, v roce 1964, Clarke a Wright navrhli účinnou heuristickou metodu, která zlepšuje přístup Dantziga a Ramsera. Po těchto dvou klíčových zpracování problému bylo v následujících desítkách let navrženo velké množství různých modelů a algoritmů pro řešení VRP. Tento zájem o VRP je způsoben jeho velkým praktickým významem v mnoha úlohách každodenního života a také jeho značnou obtížností. Nejrozsáhlejší příklady VRP, které lze vyřešit nejúčinnějšími exaktními algoritmy, obsahují přes 50 zákazníků.

Stručná historie vývoje řešení problému okružních jízd:

• 1950 - 1960 - formulace VRP (Dantzig a Ramser) - řešeny malé problémy (10 - 20 zákazníků),
• 1960 - 1970 - navrženy počátečnní konstrukční heuristiky (Clarke a Wright) - řešeny problémy s 30 - 100 zákazníky,
• 1970 - 1980 - navrženy dvoufázové heuristiky (Gillet a Miller) - řešeny rozsáhlejší problémy s 100 - 1000 zákazníků, problémy s 25 - 30 zákazníky řešeny pomocí exaktních metod,
• 1980 - 1990 - navrženy postupy založené na matematickém programování (Fisher, Jaikumar) - problémy s cca 50 zákazníky řešeny exaktními metodami,
• 1990 - 2000 - řešeny problémy s 50 - 100 zákazníky pomocí exaktních metod, na problém okružních jízd jsou aplikovány metaheuristiky.

V úlohách diskrétní optimalizace je často množina všech přípustných řešení velmi rozsáhlá. Dle teorie složitosti se rozlišuje několik tříd úloh. Většina dnes používaných algoritmů má polynomiální časovou složitost. Problémy, které tyto algoritmy řeší, řadíme do třídy P (zvládnutelné). Mezi úlohy s touto složitostí řadíme z dopravy například úlohu hledání minimální kostry grafu nebo problém nejkratší cesty v grafu.

Problémy, které nepatří do třídy P, označujeme jako nezvládnutelné. Tyto úlohy mají často důležité praktické využití, ale možnost najít optimální řešení existuje pouze pro malé vstupy. Úlohy tohoto typu mohou mít astronomický počet řešení, je proto velice obtížné získat řešení v reálném čase. V těchto situacích lze použít aproximační algoritmy, heuristiky nebo metaheuristiky. V dopravě patří do této skupiny úloh například problém obchodního cestujícího, problém okružních jízd, lokační úlohy, čínský pošťák. Tabulka 4 ukazuje různé typy úloh, jejich označení a výpočetní náročnost.

Tabulka 4: úlohy, jejich označení a výpočetní náročnost (zdroj: Lenstra, Kan, 1981)

název	zkratka	výpočetní náročnost
Traveling salesman problem	TSP	NP-hard
Directed traveling salesman problem	DTSP	NP-hard
Chinese postman problem	CPP	NP-hard
Directed Chinese postman problem	DCPP	\(O(v^{3})\)
Mixed Chinese postman problem	MCPP	NP-hard
Rural postman problem	RPP	NP-hard
Directed rural postman problem	DRPP	NP-hard
Stacker - Crane problem	SCP	NP-hard

6.7.1 Formulace problému okružních jízd

Problém okružních jízd může být popsán jako úloha, jejímž cílem je určení takových tras vozidel, aby byli obslouženi všichni zákazníci a aby celkové náklady byly minimální. Každá trasa začíná v depu, obslouží několik zákazníků a vrací se zpět do depa. Každý zákazník musí být v rámci některé trasy obsloužen právě jednou. Celková velikost dodávek zákazníků na jedné trase nesmí přesáhnout kapacitu vozidla (Capacitated Vehicle Routing Problem - CVRP).

Úloha okružních jízd je zobecněním úlohy obchodního cestujícího. Oproti němu má ale VRP řadu dalších omezení a podmínek, které úlohu blíže přizpůsobují požadavkům a problémům reálného světa. Distribuce například může probíhat z více dep, každý zákazník musí být obsloužen v daném časovém intervalu (časovém okně), může být homogenní nebo heterogenní vozový park, nebo může být dán maximální možný počet obsloužených míst v rámci jedné trasy vzhledem ke kapacitám vozidel a požadavkům zákazníků. Úloha může mít podle druhu a množství omezení hodně podob, pro lepší přehled mohou být charakteristické znaky a podmínky úlohy klasifikovány následovně:

Čas uspokojování požadavků

• čas je pevně určen (úloha rozvrhování),
• čas je dán časovým intervalem (časovými okny),
• čas není určen.

Počet středisek (dep)

• jedno středisko,
• více středisek.

Typ vozového parku

• homogenní,
• heterogenní.

Velikost vozového parku

• jedno vozidlo,
• více vozidel,
• neomezený počet vozidel.

Povaha požadavků

• deterministické - přesně známy,
• stochastické - nejsou předem známy.

Poloha požadavků v dopravní síti

• v uzlech (obsluha vrcholu sítě – rozvoz zboží),
• na úsecích (obsluha hran sítě – kropení ulic, zimní posyp silnic),
• v uzlech i na úsecích.

Typ dopravní sítě

• orientovaná,
• neorientovaná,
• smíšená.

Maximální doba pro projetí jedné trasy (pracovní doba řidičů)

• stejná pro všechna vozidla (homogenní park),
• každé vozidlo má obecně jinou dobu,
• není zadána (bez omezení).

Operace prováděné u zákazníků

• pouze nakládka (svozové úlohy),
• pouze vykládka (rozvozové úlohy),
• obě operace.

Kritérium kvality řešení (účelová funkce) * minimální součet ohodnocení úseků projetých vozidly (délka trasy, pracovní doba, spotřeba pohonných hmot), * minimální počet tras (počet použitých vozidel, pořizovací náklady), * smíšené kritérium (celkové náklady), * minimaxové kritérium.

Matematický model VRP

Mějmě úplný graf \(G=(V,H)\), kde \(V=(u_1,u_2,\dots, u_n)\) je množina zákazníků a \(H\) je množina hran spojující tyto zákazníky. Umístění depa je reprezentováno vrcholem \(u_0\) a rozmístění zákazníků je dáno vrcholy \(u_i\), kde \(i=1,2,\dots, n\). U těchto zákazníku vzniká požadavek na obsluhu určitého množství elementů. Hrana mezi každými dvěma vrcholy \(u_i\) a \(u_j\) je ohodnocena velikostí \(c_{ij}\), představuje vzdálenost, kterou musí vozidlo mezi těmito vrcholy urazit. Pro obsluhu zákazníků je k dispozici množina vozidel \(K\) o kapacitě \(C\) a trasa každého vozidla začíná a končí v depu. Každý zákazník ui má poptávku \(d_i\). Cílem je navrhnout takové trasy vozidel, aby byl požadavek v každém místě uspokojen právě jednou a aby jejich celková délka byla minimální.

Ze zadání úlohy vyplývá, že úloha má dvě podmínky přípustnosti jejího řešení:

• každý zákazník musí být v rámci některé trasy obsloužen právě jednou;
• musí být respektována kapacita obsluhujících vozidel

Pro sestavení modelu je potřeba definovat proměnné. Bivalentní proměnná \(x_{ijk}\), kde \(x_{ijk}\in\{0,1\}\) pro každé vozidel \(k\in K\) a každou dvojici objektů \((i,j)\) udává, zda je vozidlo přiřazeno na hranu \((i,j)\). Pokud dojde k přiřazení vozidla na hranu \((i,j)\), je \(x_{ijk}=1\), v opačném případě \(x_{ijk}=0\).

Matematický model VRP lze pak zapsat (Janáček, 2006):

minimalizovat \(\sum\limits_{k\in K}\sum\limits_{i\in V}\sum\limits_{j\in V} c_{ij}x_{ijk}\qquad\qquad (1)\)

za podmínek:

\(\sum\limits_{k\in K}\sum\limits_{i\in V} x_{ijk}=1\qquad u\in V,\ i\neq j\qquad\qquad (2)\)

\(\sum\limits_{u\in V} x_{ijk}=\sum\limits_{i\in V} x_{ijk}\qquad u\in V\cup\{u_0\},\ k\in K,\ i\neq j\qquad\qquad (3)\)

\(\sum\limits_{u\in V} d_i \sum\limits_{i\in V} x_{ijk}\leq C_k\qquad k\in K,\ i\neq j\qquad \qquad (4)\)

\(\sum\limits_{j\in S}\sum\limits_{i\in S} x_{ijk}\leq C_k\qquad k\in K,\ S\subseteq V,\ |S|\geq 2,\ i\neq j\qquad \qquad (5)\)

\(x_{ijk}\in \{0,1\}\qquad k\in K, \ i\in V\cup\{u_0\},\ j\in V\cup\{u_0\},\ i\neq j\qquad\qquad (6)\)

Účelová funkce této úlohyvy (1) jadřuje celkovou ujetou vzdálenost. Podmínky (2) zabezpečují, aby každý zákazník byl navštíven právě jednou jedním vozidlem. Podmínky (3) zajišťují, že každé vozidlo, které vjede do vrcholu ui, z něho také vyjede. Podmínky (4) zabezpečují, že požadavky zákazníků přiřazených vozidlu k nepřesáhnou jeho kapacitu C, a podmínky (5) určují to, že trasa vozidla musí tvořit kružnici v grafu a tato kružnice musí procházet umístěním depa \(u_0\). Tyto podmínky se označují jako anticyklící. Podmínky (6) jsou podmínky celočíselnosti.

6.7.2 Varianty úlohy VRP

Dle množství a druhu různých omezujících podmínek může mít úloha okružních jízd mnoho podob. V této části práce budou představeny některé modifikace úlohy VRP, které můžeme díky použití těchto podmínek získat ze základní úlohy okružních jízd.

Úloha okružních jízd s časovými okny

Úloha okružních jízd s časovými okny je důležitým zobecněním úlohy okružních jízd. Původní úloha se rozšíří o tzv. časová okna, která reprezentují určitý časový interval, ve kterém je nutné (možné) zákazníka obsloužit. Aby bylo možné dodržovat časové intervaly, musí být znám časový okamžik, kdy vozidlo opustí sklad, doba jízdy mezi jednotlivými vrcholy a čas nutný k vykládce (nakládce) zboží. Obsluha daného zákazníka pak musí začít během stanoveného časového okna. Velikost a počet definovaných časových oken může potom výrazně zvýšit složitost řešení takové úlohy.

Úloha okružních jízd s heterogenní flotilou vozidel

Vozidla mohou být heterogenní z různých úhlů pohledu. Typickým příkladem je flotila vozidel s odlišnou kapacitou. Vozidla mohou být různého typu (krytá, nekrytá ložná plocha), mohou mít odlišné cestovní doby, různé doby pro vykládku a nakládku zboží nebo různé další vlastnosti a charakteristiky.

Úloha okružních jízd s více středisky obsluhy

V běžně řešených úlohách se často setkáváme s více než jedním depem. Zákazníci jsou obsluhováni několika depy, kde každé má svou vlastní flotilu vozidel. Obvykle se předpokládá, že se vozidla vrací do depa, ze kterého vyjela. Tato střediska obsluhy jsou utonomní s vlastní množinou zákazníků, které obsluhují. Někdy je však pouze požadováno, aby se počet přijíždějících vozidel rovnal počtu vozidel, která depo opustila. Jednotlivá vozidla mohou po obsluze zákazníků skončit v jiném depu, než ze kterého vyrazila.

Stochastická úloha okružních jízd

Stochastická úloha okružních jízd se vyznačuje tím, že alespoň jedna část poptávky úlohy je náhodná. Jedná se například o tyto případy:

• zákazník je v úloze přítomen či nepřítomen s určitou hodnotou pravděpodobnosti,
• poptávka každého zákazníka má náhodnou velikost,
• čas obsluhy a cestovní doba jsou také náhodné proměnné.

Trasy musí být navrženy před tím, než je známa skutečná poptávka. Stochastické úlohy jsou řešeny dvoufázově. Nejprve se řešení vypočte za použití náhodných proměnných a poté, ve druhé fázi, kdy jsou hodnoty náhodných proměnných již známé, je proveden opravný (upřesňující) výpočet.

Úloha okružních jízd obsahující svoz a rozvoz

U klasické úlohy okružních jízd buď zboží zákazníkům rozvážíme, nebo ho naopak stahujeme zpět. V tomto případě však můžeme dělat obě činnosti najednou. Je třeba dbát na to, že zboží naložené u zákazníka nesmí přesáhnout kapacitu vozidla. V jednoduché verzi tohoto problému musí proběhnout nejprve rozvoz a vozidla musí být před zahájením fáze sběru zcela prázdná. V tomto případě mohou být zákazníci rozděleni do dvou tříd: množina zákazníků, kterým rozvážíme, a množina zákazníků, od kterých svážíme. Odstraněním všech hran orientovaných od svozových zákazníků k rozvozovým zajistíme, že bude nemožné obsloužit rozvozového zákazníka po zákazníkovi, od kterého svážíme. Cílem je určit množinu tras, které zajistí doručení zboží zákazníkům a odvoz od zákazníků, tak, že kapacita vozidel není překročena a celková ujetá vzdálenost je minimální.

6.7.3 Metody řešení VRP

Základní druhy metod pro řešení VRp mohou být klasifikovány následovně:

• exaktní metody,
• heuristiky,
• metaheuristiky.

Exaktní metody

Výhodou exaktních metod je jejich přesnost, jelikož jsou prověřovány všechny varianty řešení a z nich je vybráno optimální řešení. Exaktní algoritmy u kombinatoricky složitých úloh bohužel zvládají v rozumném čase pracovat jen s malými úlohami. Pro úlohy většího rozsahu je nelze použít, protože pomocí těchto algoritmů není možné v reálném čase nalézt řešení. Počet operací nutných k získání optimálního řešení roste kombinatoricky s velikostí úlohy. Jedná se především o metody větví a hranic a větví a řezů.

Metoda větví a hranic je založena na opakování dvou operací - větvení a omezování. Větvením se množina přípustných řešení rozkládá na navzájem disjunktní podmnožiny (větve). Pro každou podmnožinu vzniklou větvením se omezováním určí dolní mez (u minimalizačních úloh). Lze tak určit, které podmnožiny budou nejpravděpodobněji obsahovat optimální řešení a které naopak není třeba dále zkoumat. Algoritmus proto neprohledává množinu všech přípustných řešení, ale je založen na prohledávání množiny přípustných řešení ve směru největšího zlepšení účelové funkce, což je výhodou této metody. Pro další větvení je vybrána podmnožina s nejnižší dolní mezí. Cílem je nalézt takové přípustné řešení, pro které není hodnota účelové funkce větší než dolní mez u všech dosud nerozložených podmnožin. Výsledkem metody větví a hranic je nalezení optimálního řešení.

Heuristické metody

Heuristické metody lze v praxi využívat k řešení poměrně rozsáhlých úloh a výsledek je získán v reálném čase. Nevýhodou ovšem je, že tyto metody nezaručují nalezení optimálního řešení. Výsledkem je jedno z přípustných řešení, tedy řešení suboptimální. U něho většinou nelze zjistit, jak je vzdálené od řešení optimálního. Vzhledem k rychlosti výpočtu a nárokům na výpočetní techniku mohou být suboptimální řešení považována za přijatelná.

Heuristiky mohou být děleny do následujících dvou skupin:

• Primární heuristiky - postup začíná přípustným řešením, které je postupně zlepšováno a jehož hodnota lokálního kritéria je menší než hodnota lokálního kritéria předchozího řešení. Proces zlepšování končí dosažením takového řešení, které nejde již nadále zlepšit.
• Duální heuristiky - vytváří nejdříve nepřípustné řešení, které má hodnotu účelové funkce lepší, než může nabývat optimální řešení. Toto řešení je postupně upravováno tak, aby se odstranilo narušení podmínek přípustnosti při co nejmenším zhoršení účelové funkce v jednotlivých krocích. Výpočet končí nalezením přípustného řešení, nebo v případě, kdy dalšími možnými změnami nelze získat lepší řešení.

Oba uvedené postupy se mohou vzájemně kombinovat. Duální heuristika může poskytnout výchozí řešení, které je dále zlepšováno použitím primární heuristiky.

Heuristických metod a jejich modifikací existuje velký počet a můžeme je klasifikovat dle mnoha kritérií a přístupu k jejich řešení. Základní rozdělení může být následující:

• konstrukční heuristiky,
• dvoufázové heuristiky,
• zlepšovací heuristiky.

Heuristické algoritmy, kde je množina tras vytvářena od začátku, nazýváme konstrukční heuristiky. Zlepšovací heuristiky jsou ty, které se pokouší vytvořit vylepšené řešení na základě již existujícího řešení. Níže bude představeno několik heuristických metod, které mohou být použity k řešení úloh okružních jízd.

Dvoufázové metody

Tyto metody, kterým se věnovali M. L. Fisher a R. Jaikumar, danou úlohu nejdříve rozdělí na dvě části, na úlohu shlukování a úlohu trasování:

• metody primárního shlukování - v první fázi dojde ke zjednodušení úlohy zanedbáním podmínek souvisejících s vlastní trasou vozidla. Řeší se pouze úloha rozdělení zákazníků do shluků, aby každý shluk bylo možné obsloužit jedinou okružní jízdou vozidla. Ve druhé fázi se na jednotlivé shluky.
• metody primárního trasování - nejdříve dojde ke zjednodušení úlohy zanedbáním kapacitních omezení jednotlivých vozidel. Tím úloha přejde na rozsáhlou úlohu obchodního cestujícího, která je řešena některou z heuristických metod. Ve druhé fázi je potom získaná trasa upravována tak, aby vznikl potřebný počet okružních jízd, které respektují omezené kapacity vozidel.

Metody výhodnostních koeficientů a vsouvání

Tyto metody mohou být založeny jak na primárním tak i na duálním principu. Duální heuristiky budují trasu vozidel postupným vsouváním zákazníků do současné nepřípustné trasy. V případě primárních heuristik je nové přípustné řešení získáváno spojením dvou nebo více okružních jízd do jedné. Podle lokálního kritéria je pro úpravu řešení vybráno vložení vhodného zákazníka nebo spojení jízd. Jako lokální kritérium je použita hodnota koeficientu odhadujícího důsledky výběru pro hodnotu účelové funkce. Takto vytvořené lokální kritérium se nazývá výhodnostím koeficientem. Mezi nejznámější metody s výhodnostními koeficienty patří konstrukční heuristika, kterou vytvořili G. Clarke a J. Wright.

Výměnné metody

Princip výměnné heuristiky spočívá v tom, že jistá část objektů trasy je vyjmuta ze současného řešení a buď je vložena na jiné místo trasy, nebo je nahrazena podmnožinou objektů z množiny nezařazených objektů. Vyjmuté objekty ze současného řešení jsou následně vloženy do množiny nezařazených objektů. Kritériem, kterým je posuzován výsledek, je například změna hodnoty účelové funkce současného řešení. Výměnnou heuristikou se zabývali B. E. Gillet a L. R. Miller.

Metaheuristiky

Všechny výše uvedené heuristiky mají jednu nevýhodu, kterou je neschopnost opustit lokální minimum poté, co ho předchozími kroky dosáhnou. Metaheuristiky se vyznačují tím, že je možné za určitých okolností opustit lokální minimum a přejít posloupností iteračních kroků do jiných částí množiny přípustných řešení. Zde je šance nalézt řešení s lepší hodnotou účelové funkce, než mělo nalezené lokální optimum. Metaheuristiky také nezaručují nalezení optimálního řešení úlohy (Janáček, 2006).

Metaheuristiky jsou výkonné techniky, které se používají na výpočet náročných a rozsáhlých úloh. Mezi základní metaheuristiky se řadí simulované žíhání, Tabu search, mravenčí kolonie a genetické algoritmy.

Simulované žíhání

Název a princip této metody je inspirován fyzikálním procesem známým jako žíhání. Při tomto procesu je materiál zahříván až do kapalného stavu a poté je ochlazován zpět do stavu pevného a přitom se mění jeho krystalická mřížka. Při zahřátí jsou atomy volné a náhodně kmitají mezi stavy s vyšší energií. Když dochází k pomalému ochlazování, kmitání se zmenšuje a materiál má tendenci ztuhnout ve struktuře s vydáním minimální energie. Pro účely algoritmu nahrazuje energii minimalizační funkce.

V každém kroku algoritmu se náhodně vybere nějaký stav z blízkého okolí současného stavu řešení. Uskutečnění přechodu do nového řešení z okolí je založeno na výsledku náhodného pokusu. V případě, že je řešení lepší, je následně považováno za nové nejlepší řešení. Pokud je ale horší než řešení současné, je přijímáno pouze s určitou pravděpodobností. Pravděpodobnost přijetí je určena teplotou, která se postupně snižuje. Postupně s teplotou klesající k nule se tak algoritmus blíží ke stavu minimalizující danou funkci. Metodou se zabýval například I. H. Osman.

Tabu search

Tabu search, neboli tabu prohledávání, je metoda, kterou představil koncem osmdesátých let minulého století F. Glover. Tato metaheuristika je velmi flexibilní a dává výsledky, které jsou lepší nebo podobné výsledkům, které poskytují nejlepší heuristiky. Tato metoda se řadí mezi algoritmy lokálního prohledávání.

V každé iteraci jsou prohledána okolní řešení aktuálního řešení a nejlepší nalezené řešení nahradí to původní. Aktuální řešení je nastaveno jako nejlepší i v případě, že hodnota účelové funkce není nižší. Díky tomu je algoritmus schopen vystupovat z lokálních minim. Hlavní myšlenkou metody Tabu search je tabu list. Do tohoto listu jsou zapisována řešení algoritmu. Tím je zabráněno zacyklení neboli opakovanému nacházení nedávno vybraných řešení. Tabu list se v průběhu chodu algoritmu mění a udává řešení, která nejsou přijatelná v dalších několika iteracích. Tabu list často obsahuje pouze zakázané pohyby. Povolit tento pohyb má smysl, když jeho pokračování vede ke zlepšení celkového nejlepšího řešení. Aspirační kritéria jsou kritéria, která umožňují povolit pohyb zakázaný v tabu listu. Důležitým parametrem je délka tabu listu, protože příliš krátká délka může vést k zacyklení. V případě příliš dlouhého tabu listu může dojít k přeskočení řešení, která by mohla vést k nejlepšímu řešení.

Genetické algoritmy

Genetické algoritmy jsou pravděpodobnostní vyhledávací metody, které vycházejí z evolučního přístupu, který lze nasadit na řešení složitých problémů. Tyto metody používají techniky, které napodobují evoluční procesy známé z biologie (přirozený výběr, křížení, mutace). Mezi průkopníky v oblasti genetických algoritmů patří americký teoretický biolog J. Holland, který studoval elementární procesy v populacích, které jsou z hlediska evoluce nepostradatelné. Na základě těchto výzkumů v roce 1975 navrhl genetický algoritmus jako abstrakci daných biologických procesů.

Genetické algoritmy pracují s celou množinou řešení zvanou populací, ne pouze s jedním řešením jako metody simulované žíhání nebo Tabu search. Práce genetického algoritmu začíná vytvořením počáteční populace, tedy množiny přípustných řešení, a aktualizací dosud nejlepšího nalezeného řešení. Nová řešení se získají použitím genetických operátorů (selekce, křížení, mutace) na potenciálních rodičích vybraných uvnitř populace. Na základě účelové funkce jsou geny jedinců kříženy. Při křížení je z dvojice genů vytvořena dvojice jiná. Místo křížení je vybráno náhodně a každý z genů je na tomto místě rozdělen na dvě části. Tyto části jsou do nových genů kombinovány tak, že nový gen bude tvořen počáteční částí jednoho a koncovou částí druhého z původních genů. Nově vzniklí jedinci jsou mutováni. Při mutaci je s určitou pravděpodobností na jednom genu změněna hodnota některé složky. Na nově vzniklé populaci je provedena selekce, díky které je populace omezena na zvolený počet jedinců. Probráním nové populace je aktualizováno dosud nejlepší nalezené řešení a celý proces je opakován, dokud není splněna některá z podmínek ukončení.

Genetické algoritmy jsou založeny na principu, že nejlepší rodiče mají nejlepší potomky. Nejlepší členové populace mají proto velkou pravděpodobnost, že budou vybráni jako rodiče. Ti jsou pak kříženi a dávají prostor svým dětem, které nahrazují slabší jedince populace nebo rodiče samotné. Každému členovi je přechodem do nové generace určena hodnota fitness funkce (účelové funkce). Ta vyjadřuje kvalitu řešení znázorněného tímto jedincem. Postup je opakován do té doby, kdy je získána populace, která má silné všechny členy.