Kapitola 2 Interpolace prostorových dat, mapová algebra

Často se setkáváme se skutečností, že máme k dispozici údaje o daném jevu pouze prostřednictvím určitého množství bodových dat, ať už je to z důvodu náročného sběru dat, vysoké ceny nebo proto, že realizace vyčerpávajícího sběru dat je nemožná. Většinou nás ale zajímají i hodnoty v místech, kde měření provedeno nebylo. Potřebujeme znát celkové prostorové rozložení hodnot sledované proměnné, čehož docílíme interpolací známých bodových dat.

Interpolací tedy získáme tzv. mapu sledovaného jevu, která může být vyjádřena i ve formě prostorového modelu. Příkladem je klimatický model vytvořený z údajů meteorologických stanic, model terénu z nadmořských výšek nebo model ložisek nerostných surovin vytvořený na základě vrtů.

2.1 Výběr reprezentativních vzorků

Lokalizace měřených (odměrných) bodů v zájmovém území. Rozmístění (tzv. sampling) je důležité pro výběr interpolačního algoritmu a úspěšnost vlastní interpolace. Rozlišujeme rozmístění:

• pravidelné - může být zavádějící v případě zcela rovnoměrně rozmístěného jevu, který je studován (stromy, …),
• náhodné - ze statistického hlediska je korektnější. Má ale i zápory - problematická lokalizace a zaměření jednotlivých míst než u pravidelně rozmístěných uzlů mřížky. Náhodné a nerovnoměrné rozmístění nemusí vystihovat základní rysy v rozložení měřené charakteristiky a může být i nákladnější.

Rozmístění vstupních dat, se kterými se uživatel v praxi nejčastěji setkává ukazuje obrázek 2. Jako vhodný kompromis mezi pravidelným a náhodným rozmístěním je možné použít stratifikované náhodné rozmístění, kdy je zajištěno pokrytí celé zájmové oblasti (rozdělené v pravidelném rastru). Shluky (skupiny) se nejčastěji využívají při analýze prostorové variability. Specifickými problémy se potom vyznačuje interpolace na profilech a izoliniích, zvláště pokud je vyžadována extrapolace nebo je množství dat nedostatečné.

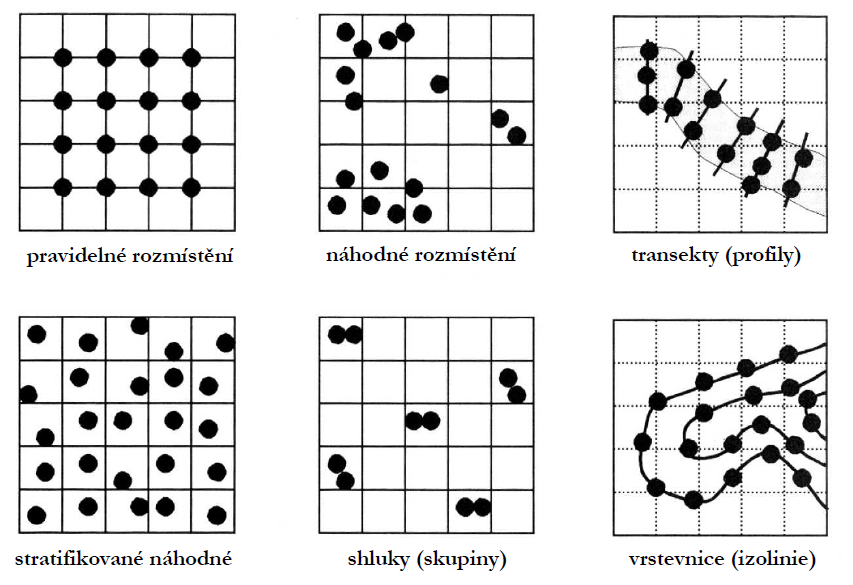
Obrázek 1: typy rozmístění vstupních dat (zdroj: upraveno podle Burrough and McDonnell, 1998)

V řadě případů je z různých důvodů (např. ekonomických, dostupnost, …) prováděno měření pouze v omezené míře (profily – transepty). Ve velké části interpolačních úloh je rozmístění měřených bodů předem dáno, bez možnosti ho výrazně ovlivnit vhodnou lokalizací a výběrem (např. síť meteorologických stanic apod.)

K prezentaci spojitých polí lze využít: grid, TIN, izočáry či areály.

Možné datové zdroje pro interpolaci:

• bodová měření v terénu,
• digitalizované izolinie či polygony,
• stereopár leteckých fotografií či družicových obrazových záznamů.

Předpoklady úspěšné prostorové interpolace lze představuje splnění těchto podmínek:

• existence dostatečně reprezentativního vzorku měřených dat,
• vhodné vlastnosti měřené veličiny a typ dat (ordinální, intervalová, poměrová),
• teoretické i empirické znalosti o povaze prostorové diferenciace studovaného jevu,
• znalost podstaty použitelných interpolačních metod,
• znalost způsobu výběru nejvhodnější metody.

Velmi důležitou fází interpolace je provedení tzv. průzkumové (explorační) analýzy prostorových dat (ESDA). Jejím cílem je zjistit základní informace o charakteru vstupních dat. Jedná se např. o prověření požadavků normality, stacionarity apod. ESDA většinou představuje analýzu rozdělení hodnot - analýzu histogramu, výpočet základní popisné statistiky včetně momentů vyššího řádu (asymetrie a špičatosti), analýzu kvantilového grafu (Q-Q grafu), případná transformace (log), zkoumání odlehlých hodnot a jejich případné odstranění, analýza trendu (a jeho případné odstranění u interpolačních metod, které to vyžadují). ESDA je nezbytným předstupněm úspěšné aplikace metod krigingu.

Běžné problémy interpolace, se kterými je možné se setkat: * vymezení studované plochy – přirozené a administrativní hranice, * dostupnost bodů měření vně studované plochy.

2.2 Interpolace bodových dat

Termín interpolace bodových dat vyjadřuje proces výpočtu neznámých hodnot určitého jevu na základě známých bodových dat. Tato práce se zabývá případem, kdy body leží v dvourozměrném prostoru. Místo označení interpolace se často také používá pojem odhad nebo predikce neznámých hodnot. Aby bylo možné bodová data interpolovat, musí být splněna podmínka, že určitý sledovaný jev je spojitý nebo prostorově závislý (autokorelovaný).

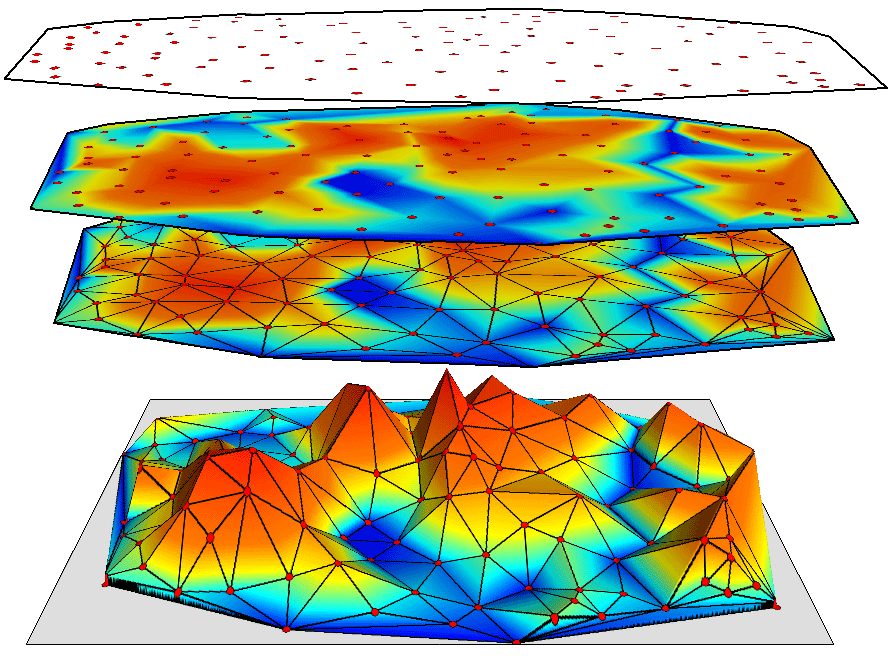
Obrázek 2: interpolace bodových dat (zdroj: https://www.geosolutions.com/3d/analyse/images/)

K interpolaci se váže pojem extrapolace. Rozdíl mezi těmito postupy je v tom, že při interpolaci odhadujeme neznámé hodnoty v rámci tzv. prostorové domény známých údajů, zatímco při extrapolaci odhadujeme hodnoty mimo její rozsah. Extrapolace je obecně méně přesný postup, kterému je doporučeno se spíše vyhnout, důvodem je například možnost získání záporných odhadů striktně pozitivní proměnné.

2.2.1 Interpolační metody

2.2.1.1 Klasifikace interpolačních metod

Interpolační techniky lze rozdělovat podle různých hledisek:

A. Podle prostorových entit, na které jsou aplikovány - interpolace:

• bodů
• linií
• ploch

B. Deterministické a stochastické metody

Deterministické metody lze využít v případech, kdy existuje dostatek informací o prostorovém chování studovaného jevu, které dovolují ho popsat matematickou funkcí. Tyto metody umožňují extrapolaci za hranice vymezené měřenými vzorky. Deterministická extrapolace je však možná pouze za předpokladu, že máme na zřeteli fyzikální podstatu jevu (např. záporné hodnoty atmosférických srážek apod.).

Stochastické modely – zahrnují koncept náhodnosti za předpokladu, že hodnoty interpolovaného povrchu z daného měřeného vzorku jsou jen jednou z nekonečného množství možných variant. Do skupiny těchto metod patří např. metody krigingu či analýza trendu.

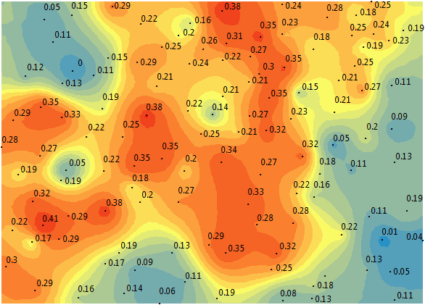
Obrázek 3: stochastická interpolace - kriging (zdroj: https://gisgeography.com/kriging-interpolation-prediction/)

C. Globální a lokální metody

Uvedené hledisko zohledňuje způsob, jakým daná metoda nakládá se vstupními daty (měřenými vzorky).

Globální interpolace – aplikují jednu funkci na všechny měřené body ve studované ploše. Využívají princip průměrování, redukují vliv bodů s extrémními hodnotami. Produkují hladké povrchy bez náhlých zlomů.

Globální metody využívají všech měřených bodů. Bývají používány k vystižení obecných tendencí v měřených datech - trendů, jako předstupeň vlastní interpolace lokálními interpolátory, které interpolují rezidua - zbytek po odečtení trendu. Do této skupiny lze zařadit také klasifikační metody, které využívají všech dostupných informací k rozdělení studované oblasti do regionů, ve kterých je potom hodnota interpolovaného jevu charakterizována statistickými momenty (průměrem, rozptylem), určenými z měřených bodů v rámci každého regionu.

V závislosti na tom, co představuje nezávisle proměnnou lze globální modely interpolace dělit do dvou skupin:

• První skupinu tvoří modely, u nichž nezávisle proměnnou jsou pouze souřadnice měřených bodů interpolovaného atributu. Tyto metody se označují jako analýza trendu (trend surface analysis).
• Druhou skupinu globálních metod tvoří regresní modely. Zkoumají vztahy mezi atributy, které jsou pro dané území známé či dají se snadno změřit a atributem, jehož hodnoty jsou pro danou plochu interpolovány. Sestavený regresní model může mít podobu jednoduché i vícenásobné regrese a označuje se také jako funkce transferu (např. sestavení pole teplot na základě nadmořských výšek.

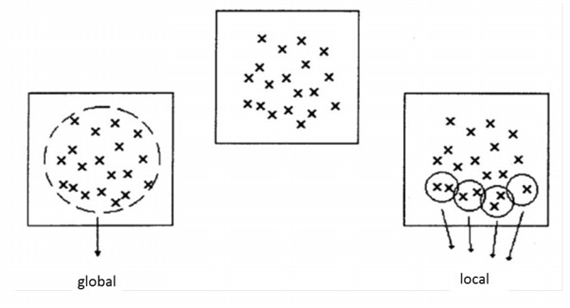
Obrázek 4: globální a lokální metody interpolace

Lokální metody interpolace aplikují stejnou interpolační funkci opakovaně na malou část měřených dat. Tato malá část vzorků představuje okolí interpolovaného bodu. Definování okolí bodů (velikosti, tvaru) je podstatným problémem lokálních metod. Přes definici okolí mohou lokální metody přecházet v globální. Lokální techniky lze definovat také jako postupy, u kterých je nutné provést více než jeden běh algoritmu se vstupními daty.

Příklady lokálních interpolací: thiessenovy polygony, klouzavé průměry, kriging.

Příklady globálních interpolací: analýza trendu, fourierovy analýzy.

D. Exaktní a aproximující metody

Metody exaktní interpolace ve výsledném povrchu zachovávají hodnoty v bodech měření.Jsou vhodné v případech, kdy existuje vysoká pravděpodobnost, že měřené hodnoty jsou správným nestranným odhadem měřené veličiny.

Obrázek 5: exaktní interpolace (zdroj: http://www.gisresources.com/classification-of-interpolation_2/)

Aproximační metody nahrazují hodnoty v měřených bodech hodnotou vypočtenou, která se více méně liší od hodnoty měřené a je výsledkem použitého algoritmu. Jsou vhodné v případech, kdy existuje jistá míra nejistoty o naší schopnosti naměřit stejnou hodnotu v případě opakovaného měření v tomtéž bodě.

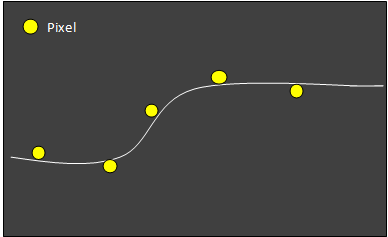
Obrázek 6: aproximační interpolace (zdroj: http://www.gisresources.com/classification-of-interpolation_2/)

Příklady exaktních interpolací: line threading, thiessenovy polygony, kriging.

Příklady aproximujících interpolací: Analýza trendu, klouzavé průměry a všechny druhy založené na filtracích.

E. Metody spojité (gradual) a zlomové (abrupt)

Kritériem dělení je spojitost interpolovaných hodnot. Spojité interpolátory produkují hladké povrchy na rozdíl od zlomových (thiessenovy polygony, generování obalových zón – bufferu). I spojité metody interpolace lze omezit tzv. bariérami (srázy a zlomy při modelování terénu, atmosférické fronty při modelování některých polí met. prvků).

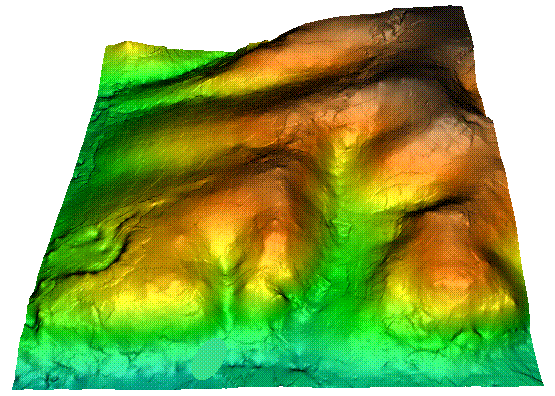
Obrázek 7: spojitá interpolace (zdroj: http://www.gisresources.com/classification-of-interpolation_2/)

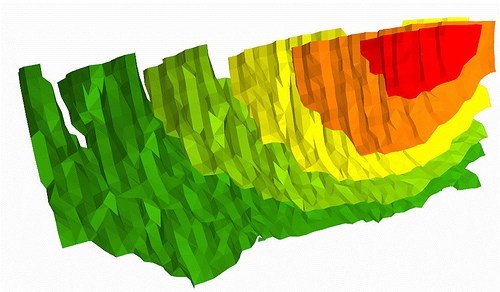
Obrázek 8: zlomová interpolace (zdroj: http://www.gisresources.com/classification-of-interpolation_2/)

2.2.1.2 Přehled interpolačních metod

2.2.1.2.1 Metody analogové interpolace (line thrading or eye balling)

Jedná se o metody vytváření izolinií na základě spojování míst s obdobnými hodnotami jevu založené na expertním odhadu (geolog, synoptik). Dále využívají empirie, obecné teorie a znalosti místních zvláštností (budování expertních systémů). Základní omezení (s ohledem na počítačové zpracování):

• problém zpracování velkého množství bodů,
• problém subjektivního přístupu,
• problém časové náročnosti.

2.2.1.2.2 Globální interpolátory

Globální interpolátory využívající klasifikačních modelů a ANOVA analýzy

Jsou založeny na podmínce stacionarity výběru. To je předpoklad, že míry úrovně a variability výběrového souboru nezávisí na velikosti výběru a rozmístění jednotlivých měřených bodů.

Za výše uvedeného předpokladu lze k interpolaci v rámci studovaného území využít externě definovaných prostorových jednotek (regionů). Klasifikace homogenními polygony předpokládá, že rozptyl hodnot interpolovaného atributu v rámci externě definovaného regionu je menší jak mezi dvěma regiony. Tohoto přístupu se často používá při mapování půd či landscape units, ekotopů, kde jednotlivé objekty (půdní jednotky, říční terasy, dílčí povodí, svahy, …) jsou vhodné pro definování jiných (interpolovaných) atributů o daném území.

ANOVAR model:

\[z(x_0)=\mu +\alpha_k + \varepsilon\],

kde: \(z(x_0)\) je hodnota atributu \(z\) v bodě \(x_0\), \(\mu\) je celkový průměr atributu na zpracovávaném území, \(\alpha_k\) je odchylka mezi \(\mu\) a průměrem v regionu \(k\) a \(\varepsilon\) je reziduum, šum.

Model předpokládá, že v rámci každého regionu (třídy) \(k\) mají hodnoty interpolovaného atributu normální rozdělení. Průměrný atribut pro třídu \(k\) je roven:

\[\mu +\alpha_k\]

a je určen z výběrových měření v rámci třídy \(k\). Uvedený přístup vychází z několika předpokladů:

• kolísání hodnot \(z\) v rámci jednotlivých tříd je náhodné,
• měřená hodnota v rámci každé mapované třídy se vyznačuje stejně velikou náhodnou složkou \(\varepsilon\),
• studované atributy mají normální rozdělení,
• veškeré prostorové změny se dějí na hranicích mezi jednotlivými třídami, změny se dějí skokem, ne postupně.

Nevýhody: hodnoty mohou v rámci jedné třídy kolísat více (měně) jak v rámci jiné třídy. Nelze mapovat prostorové změny ve větším měřítku. Data často nemají normální rozdělení. Potom je nutná normalizace např. pomocí transformace přirozenými logaritmy.

Globální interpolátory využívající analýzy trendu

Jestliže se určitá vlastnost v prostoru mění kontinuálně a je spojitá (teplota , nadmořská výška, apod.), lze body z tohoto povrchu interpolovat polynomickou funkcí. Body v neměřených lokalitách lze vypočítat z koeficientů, vypočtených na základě bodů měřených a souřadnic bodů neměřených (interpolovaných).

Nejjednodušší způsob - mnohonásobná regrese hodnot atributu vs. geografické souřadnice. Metodou nejmenších čtverců lze nalézt nejvhodnější koeficienty pro daný polynom n-tého řádu. Předpokládá se normální rozdělení.

Předpokládejme měření studované veličiny v transektu (profilu). Jestliže hodnoty obecně rostou či klesají (zanedbáme-li náhodná kolísání) - lze hodnoty interpolovat pomocí lineárního regresního modelu (polynomem 1. stupně):

\[z(x)=b_0 +b_1 x+ \varepsilon\],

kde: \(b_0\) a \(b_1\) jsou regresní koeficienty a \(\varepsilon\) je náhodný šum, nezávislý na hodnotách \(x\) s normálním rozdělením.

Není-li povrch rovinou, ale složitějším tvarem - lze ho interpolovat polynomem vyššího řádu, např. polynomem 2. stupně:

\[z(x)=b_0 +b_1 x+ b_2 x^2 +\varepsilon\].

Zvyšováním stupně polynomu lze vystihnout složitější tvary a redukuje se náhodná složka. Uvedené rovnice platí pro 1D, ve dvourozměrném prostoru budou v rovnici začleněny obě souřadnice \(x\), \(y\):

lineární trend: \[z(x)=b_0 +b_1 x+ b_2 y\] kvadratický trend: \[z(x)=b_0 +b_1 x+ b_2 y+ b_3 x^2 +b_4 xy+b_5 y^2\] kubický trend: \[z(x)=b_0 +b_1 x+ b_2 y+ b_3 x^2+ b_4 xy+b_5 y^2 +b_6 x^3+b_7 x^2y+ b_8 xy^2 + b_9 y^3\]

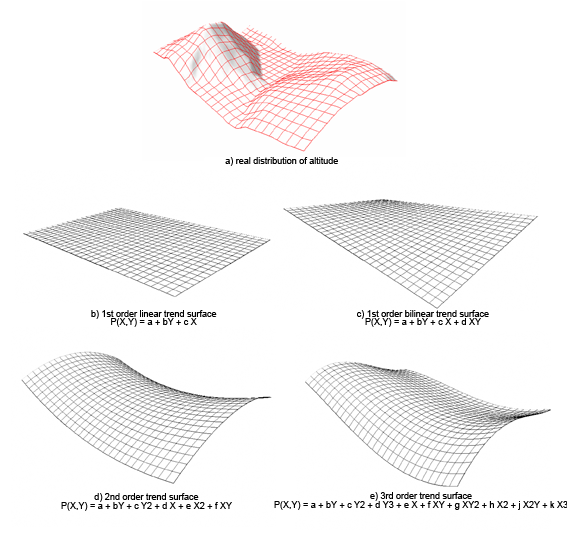
Obrázek 9: analýza trendu (zdroj: http://www.gitta.info/SpatChangeAna/en/html/spatial_dist_an_TrendSurf.html)

Trendový povrch prezentovaný polynomem vyššího řádu vykazuje značné chyby na okrajích zpracovávaného povrchu (edge effects). Mimo zpracovávané území může nabývat extrémních či dokonce záporných hodnot interpolované vlastnosti (nemajících fyzikální význam- např. záporná hodnota atmosférických srážek).

Jde o globální interpolátor, který zřídka prochází měřenými body a který shlazuje lokální odchylky. Protože lokální odchylky jsou prostorově závislé, často se tohoto postupu využívá k definování částí povrchu, které se významně odlišují od obecného trendu. Druhý častý způsob využití je odfiltrování obecného trendu a aplikace lokálních interpolátorů na reziduální složku prostorových změn studovaného jevu. Vypočtený trend lze testovat z hlediska jeho významnosti.

Pro ilustraci si to ukažme na příkladu indexu změny počtu obyvatel v letech 1900 - 1986 v 55 lokalitách distriktu Sarine (kanton Fribourg ve Švýcarsku):

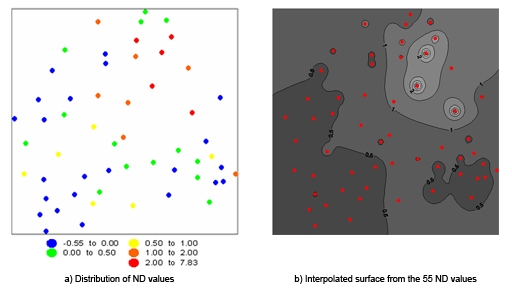
Obrázek 10: vzorek lokalit se zjištěnými hodnotami indexu (zdroj: http://www.gitta.info/SpatChangeAna/en/html/spatial_dist_an_TrendSurf.html)

Obrázek 11: trendové povrchy různého řádu modelující Index populačního růstu (zdroj: http://www.gitta.info/SpatChangeAna/en/html/spatial_dist_an_TrendSurf.html)

Globální interpolátory využívající regresní analýzy

V řadě případů existuje zřejmá vazba mezi hodnotami interpolované veličiny a vybranými jinými atributy studovaného prostoru (teplota a nadmořská výška, srážky a vzdálenost od moře, koncentrace znečištění a vzdálenost od zdroje apod.). Lze tedy sestavit empirický model závislosti interpolované veličiny na hodnotách jedné či několika veličin nezávislých. Tento model má následující obecnou formu:

\[z(x)=b_0 +b_1 P_1+ b_2 P_2+\varepsilon\],

kde: \(b_0\) … \(b_n\) jsou regresní koeficienty, \(P_1\) … \(P_n\) nezávisle proměnné a \(\varepsilon\) je náhodný šum.

Sestavení regresní závislosti je založeno na metodě nejmenších čtverců, výsledný model může být lineární i nelineární a jako nezávisle proměnné lze kombinovat geografické souřadnice s jinými atributy.

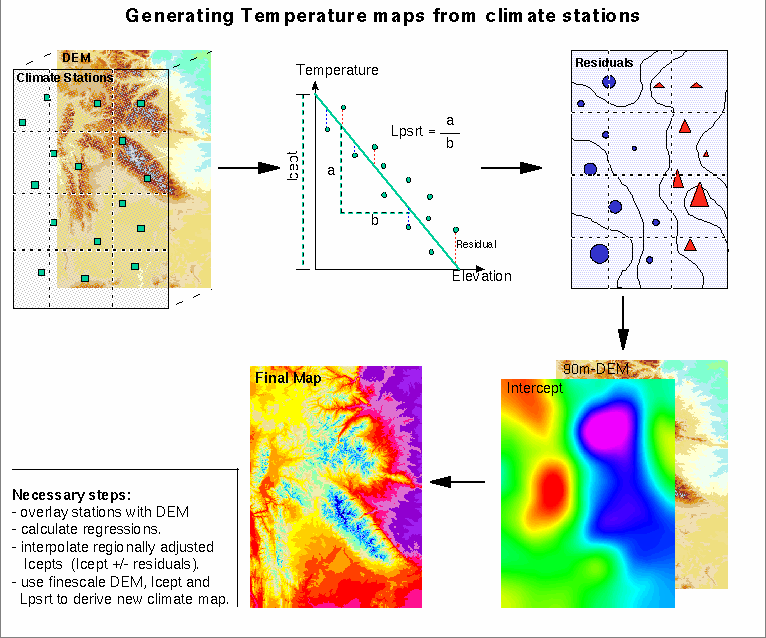
Obrázek 12: interpolace pomocí regresní analýzy (zdroj: https://www.wsl.ch/staff/niklaus.zimmermann/biophys.html)

2.2.1.2.3 Lokální interpolátory

Výše uvedené globální interpolátory považovaly lokální efekty za náhodný šum. Lokální interpolátory využívají k výpočtu hledané hodnoty pouze určitého počtu měření z předem definovaného okolí počítaného bodu. Obecný postup se sestává z následujících kroků:

1. definování velikosti a tvaru zájmového okolí,
2. nalezení měřených bodů v tomto okolí,
3. nalezení matematické funkce vystihující kolísání hodnot nacházejících se v okolí daného bodu,
4. výpočet hodnoty pro uzly regulérní sítě (grid).

Uvedený postup je opakován do té doby, dokud nejsou vypočteny hodnoty interpolované veličiny pro všechny uzly (buňky) gridu. Pro každý konkrétní postup lokální interpolace jsou důležité následující skutečnosti:

• druh použité interpolační funkce,
• velikost, tvar a orientace okolí,
• počet bodů v okolí zahrnutých do výpočtu,
• rozložení uvažovaných bodů (regulérní či nepravidelné),
• možné začlenění externí informace např. o obecném trendu.

Většina lokálních interpolátorů pracuje na principu „filtrovacího okénka“, do jisté míry počítají průměrnou hodnotu z bodů v okolí či v definované vzdálenosti.

Metoda nejbližšího souseda (Thiessenovy polygony)

Hodnoty atributů v neměřených místech jsou určeny z hodnot nejbližšího místa měřeného. Podle schématu uvedeného na obrázku je zpracovávané území rozděleno na nepravidelné trojúhelníky (Delaunay triangulace). Z nich jsou poté definovány tzv. thiessenovy polygony. V závislosti na rozmístění měřených dat mohou tyto polygony být pravidelné či nepravidelné. V GIS se často využívají jako rychlý prostředek pro vztažení bodu k určitému okolí. Celá metoda je založena na předpokladu např., že meteorologická data z určité oblasti mohou být určena z nejbližší meteorologické stanice. Tato metoda je nevhodná pro spojitě se měnící jevy (srážky, teplota, …).

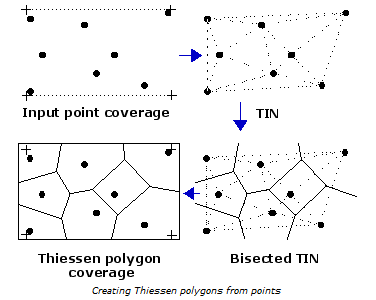
Obrázek 13: tvorba Thiessenových polygonů (zdroj: http://gisedu.colostate.edu/webcontent/nr505/2013_Projects/Team11/GISConcepts.html)

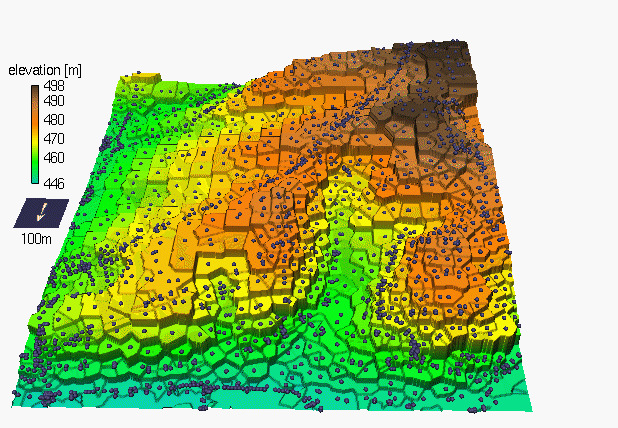
Obrázek 14: ukázka Thiessenových polygonů (zdroj: http://fatra.cnr.ncsu.edu/~hmitaso/gmslab/interp/F1a.gif)

Tvorba Thiessenových polygonů je lokální, exaktní metoda interpolace. Původně byla využívána pro plošné odhady srážek. Je to metoda robustní, vždy produkuje stejný povrch ze stejné množiny vstupních dat. Nelze při ní však použít externí informace o faktorech, které mohou ovlivňovat hodnoty v místech měření. Je vhodná k vymezování teritoria (oblasti vlivu). Forma výsledného povrchu (mapy) je determinována rozdělením původních měřených bodů. Změny v hodnotách atributů se dějí skokem, na hranicích každého polygonu. Postup však lze použít na kvalitativní data.

Metody konstrukce sítě nepravidelných trojúhelníků (TIN)

Exaktní metoda vhodná pro nepravidelně rozmístěné body měření. Tyto body jsou spojeny liniemi a vytváří síť nepravidelných trojúhelníků. Protože hodnoty v bodech na počátku a konci linií jsou známy, lze použít jednoduchou lineární závislost k interpolaci bodů mezi dvěma body na linie. TIN je metoda interpolace i způsob vizualizace spojitých povrchů. Pro některé druhy povrchů je vhodná – obecně pro povrchy které se vyznačují náhlými změnami spádu (fluviálně erodované povrchy).

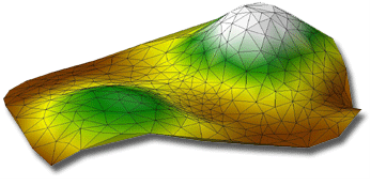
Obrázek 15: TIN (zdroj: http://wiki.gis.com/wiki/index.php/Triangulated_irregular_network)

Proces vytváření spojitého povrchu metodou nepravidelné trojúhelníkové sítě zahrnuje:

• výběr charakteristických bodů (ne z jakékoliv množiny nepravidelně rozmístěných bodů lze vytvořit TIN),
• způsob propojení bodů do trojúhelníkové sítě,
• způsob modelování povrchu uvnitř trojúhelníků.

Při výběru bodů je potřeba mít na zřeteli to, aby body by především reprezentovaly významné rysy terénu – zlomy, údolnice, hřbetnice. V závislosti na komplexnosti terénu může být hustota bodů značně proměnlivá. Algoritmy pro výběr bodů:

• algoritmus Fowler and Little,
• VIP algoritmus,
• Drop heuristic algoritmus.

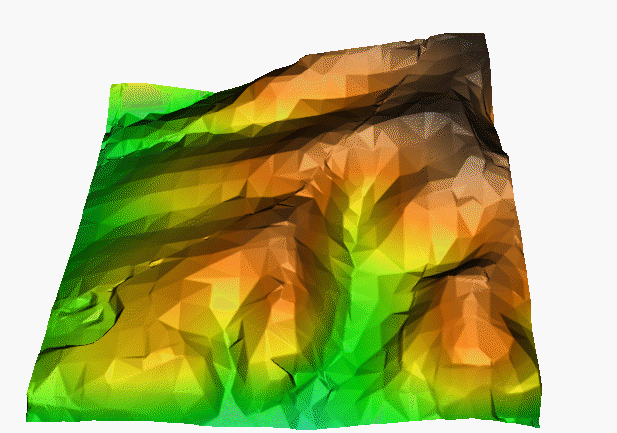
Obrázek 16: příklad povrchu vytvořeného metodou TIN (zdroj: http://fatra.cnr.ncsu.edu/~hmitaso/gmslab/interp/F1b.gif)

Způsob propojení bodů do trojúhelníkové sítě se řeší metodou Delaunay triangulace:

Tři body tvoří tzv. Delaunay trojúhelník pouze v případě, pokud kružnice, která je těmto třem bodům opsaná neobsahuje žádný další bod. Tato podmínka zaručuje, že trojúhelníky jsou přibližně rovnostranné a jakýkoliv vnitřní bod trojúhelníka je co možná nejblíže jednomu z vrcholů – tedy bodu měření. Delaunaly triangulace může být také vytvořena z thiessenových polygonů.

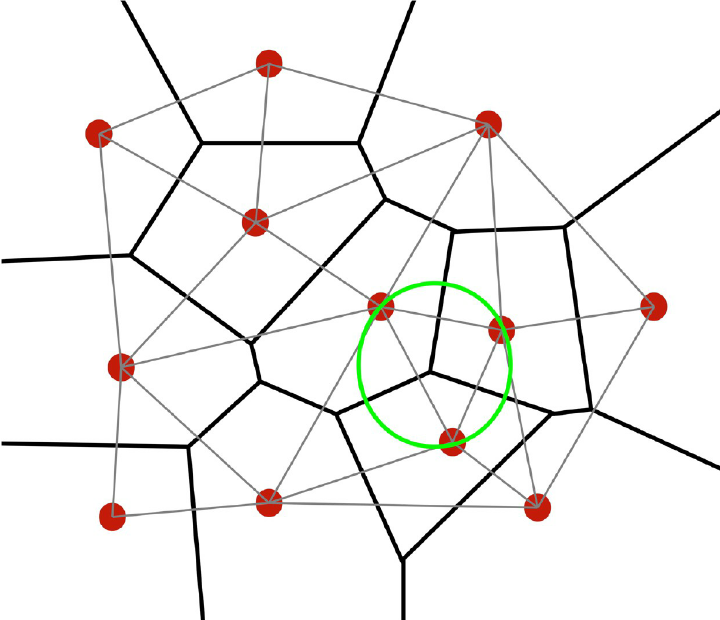
Obrázek 17: Delaunay triangulace a Thiessenovy polygony (zdroj: https://stackoverflow.com/questions/42047077/voronoi-site-points-from-delaunay-triangulation)

Metoda inverzní vzdálenosti

Tato metoda kombinuje ideu vzdálenosti využívanou v thiessenových polygonech a ideu postupných změn trendových povrchů. Je založena na předpokladu, že hodnota atributu v určitém bodě je váženým aritmetickým průměrem hodnot okolních měřených bodů. Váhy jsou určeny pro každý bod například jako inverzní vzdálenost měřeného bodu od bodu interpolovaného (čím bližší bod, tím má větší váhu). Nejjednodušším je lineární interpolátor.

Jde většinou o exaktní interpolátor. Forma výsledného interpolovaného povrchu závisí na shlucích bodů a na odlehlých měřeních. Dává nejlepší výsledky při dostatečném množství měřených bodů pravidelně rozmístěných v interpolovaném prostoru.

Obecný vzorec pro odhad hodnoty Z: \[\begin{equation} \hat{Z}=\frac{\sum\limits_{i=1}^n w_i z_i}{\sum \limits_{i=1}^n w_i}, \end{equation}\]

kde váhy \(w_i\) se určují ze vztahu \[w_i=\frac{1}{d_k}\] nebo \[w_i=e^{-d_k}\].

Hodnoty vah \(w_i\) představují funkci vzdálenosti \(d\). Hodnota exponentu \(k\) se nejčastěji volí 1 či 2 a ovlivňuje, v jakém poměru klesá hodnota váhy měřeného bodu s rostoucí vzdáleností od bodu interpolovaného.

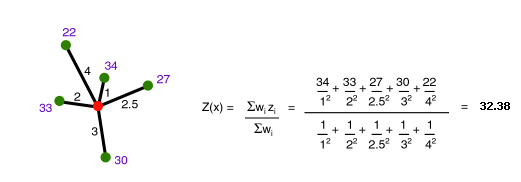
Obrázek 18: výpočet interpolované hodnoty metodou IDW (zdroj: pinterest.com)

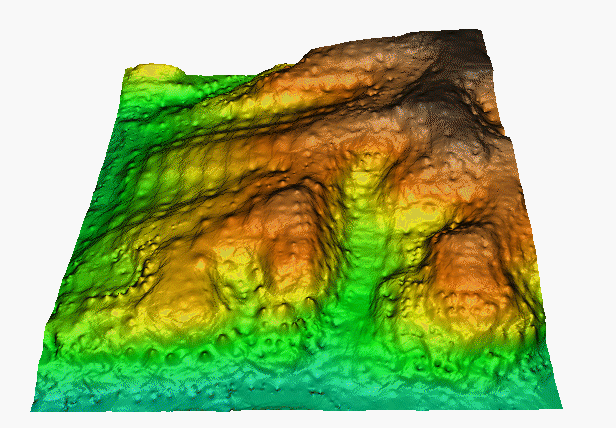
Obrázek 19: ukázka povrchu vytvořeného metodou IDW (zdroj: http://fatra.cnr.ncsu.edu/~hmitaso/gmslab/F1c.gif)

Metoda IDW často produkuje povrch, který je charakteristický koncentrickými strukturami kolem interpolovaných bodů (tzv. **„bulls eyes“**). Protože IDW je založena na lokálním průměrování, neposkytuje odhady mimo rozsah hodnot měřených bodů. Výsledkem jsou často nereálné tvary výsledného povrchu (viz obrázek 20).

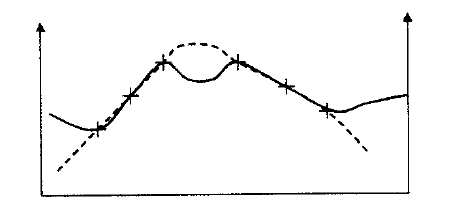
Obrázek 20: Metoda IDW - efekt „průměrování“- potlačení lokálních extrémů (zdroj: Dobrovolný, 2010)

Program ArcGIS používá modifikaci metody IDW založenou na následujícím modelu:

\[\begin{equation} \hat{Z(s_0)}=\sum\limits_{i=1}^{n} \lambda_{i}Z(s_{i}), \end{equation}\]

kde \[\lambda_{i}=\frac{d_{i0}^{-P}}{\sum\limits_{i=1}^{N}d_{i0}^{-P}}\] a \[\sum\limits_{i=1}^{n} \lambda_{i}=1\].

Váhy \(λ\) jsou v tomto případě definovány podle výše uvedeného vzorce, ve kterém exponent \(p\) vyjadřuje jejich změnu v závislosti na vzdálenosti interpolovaného bodu od bodu měřeného. Metoda dále umožňuje prostřednictvím minimalizace tzv. RMSPE (root mean square prediction error)nalézt optimální hodnotu \(p\).

Způsob definování velikosti okolí – ve většině případů se uvažuje kruhové okolí interpolovaného bodu a pro odhad hodnoty se berou všechny body bez ohledu na směr, ve kterém se nachází (povrch se považuje za izotropní). Pokud však existuje reálný předpoklad, že body v jistém směru mohou mít na interpolovanou hodnotu jinou váhu než ve směru jiném, potom může mít okolí tvar elipsy. Je-li například takovýmto vlivem převládající směr větru, potom okolí interpolovaného bodu je definováno jako elipsa, jejíž hlavní osa je rovnoběžná s tímto směrem. Předpokládáme, že v tomto směru si budou hodnoty interpolované veličiny více podobné na větší vzdálenost než ve směru kolmém.

Dále je řešena otázka počtu bodů (minimální a maximální počet bodů uvažovaných pro výpočet nové hodnoty) a také jejich rozmístění v rámci definovaného okolí. To bývá děleno na kvadranty či oktanty a takovém případě je min. a max. počet vztažen k těmto sektorům.

Metoda IDW je senzitivní na shluky měřených bodů a také na odlehlé hodnoty. Jistou nevýhodou také je, že minimální a maximální hodnota interpolované veličiny se může nacházet pouze v bodech měření (viz. dále - porovnání s metodami RBF).

Jistou modifikací výše popsané metody je tzv. Shepardova metoda. Ta navíc provádí vyrovnání interpolovaných hodnot metodou nemenších čtverců. Výsledkem je potlačení efektu koncentrických izolinií.

Prostorové klouzavé průměry

Za modifikaci metody inverzní vzdálenosti lze považovat metodu prostorových klouzavých průměrů. Nová hodnota může být prostým průměrem či váženým průměrem ale též např. modální hodnotou. Stěžejní úlohou této metody je definování velikosti, tvaru a charakteru okolí. Okolí je nejčastěji navrhováno ve tvaru kruhu či pravoúhelníka. Jako váhy se nejčastěji využívá vzdálenosti od středu definovaného okolí a váhy se mohu měnit lineárně i nelineárně. Vzhledem k často omezenému počtu bodů měření je vedle velkosti okolí důležitá otázka také počtu bodů v okolí (minimálního i maximálního). Borrough (1986) navrhuje použít 4 až 12 bodů s optimem 6 až 8 bodů. Větší počet bodů produkuje značně shlazený povrch, u malého počtu bodů dominují extrémní hodnoty.

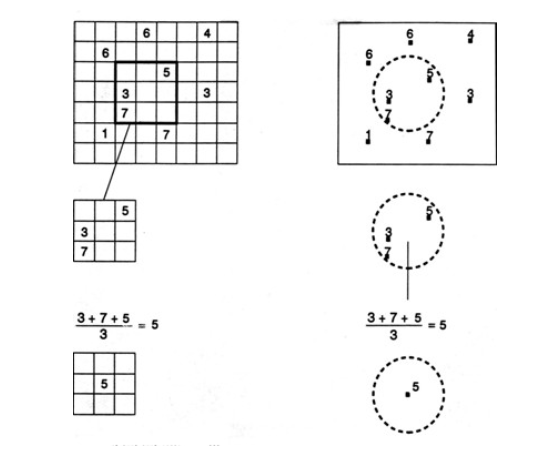
Obrázek 21: interpolace metodou prostorových klouzavých průměrů (zdroj: Dobrovolný, 2010)

Metodu prostrových klouzavých průměrů je vhodné použít za těchto podmínek:

• existuje nejistota s ohledem na reprodukovatelnost výsledků opakovaných měření v daném bodě (vlastní proměnlivost pole hodnot měření),
• samotná technická stránka měření je zatížena jistou chybou,
• je známo, že skutečné prostorové pole daného jevu vykazuje kromě obecného trendu také lokální variabilitu.

Příkladem může být měření rychlosti větru.

Interpolace metodou lokálních polynomů

Polynom \(n\)-tého stupně je aplikován ne na celý interpolovaný povrch, ale vždy na část povrchu definovanou jako okolí interpolovaného bodu přičemž tato okolí se překrývají. Stejně jako v případě IDW je specifikován tvar okolí, min. a max. počet bodů v okolí resp. rozdělení okolí na sektory. Body definovaného okolí je proložen polynom n-tého stupně a interpolovaná hodnota je použita pro střední bod okolí. V následném kroku se okolí posouvá po interpolované ploše stejně jako v případě klouzavých průměrů. Jedná se o aproximativní metodu interpolace, která však více zohledňuje lokální vlivy než metoda „globálních“ polynomů. Obrázek ukazuje v transektu čtyři kroky postupného prokládání přímky třemi nejbližšími body.

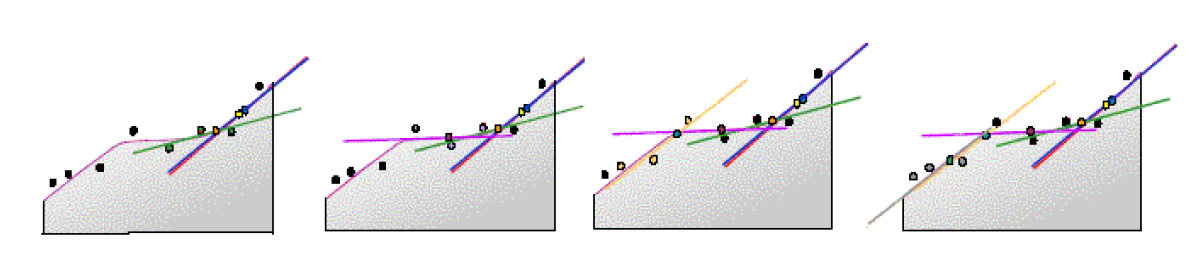
Obrázek 22: interpolace metodou lokálních polynomů (zdroj: Dobrovolný, 2010)

Model lokálních polynomů je optimalizován výpočtem RMSPE a může počítat s efektem anizotropie stejně jako v případě metody inverzní vzdálenosti. Metoda je závislá na správné volbě velikosti okolí interpolovaného bodu.

Lokální interpolátory využívající regresní analýzy

Spočívají v sestavení empirického modelu závislosti interpolované veličiny na hodnotách jedné či několika veličin nezávislých a to pro jisté okolí interpolovaného bodu. Regresní vztah je tedy na rozdíl od globální varianty této metody sestaven pouze pro body v předem definovaném okolí bodu. Interpolovaná hodnota je použita pro střední bod okolí, které se posouvá stejně jako v případě klouzavých průměrů.

Splinové funkce (piece wise polynomial function)

Splinové funkce jsou matematicky definované křivky, které po částech interpolují jednotlivé body povrchu a to exaktně, přitom navíc zajišťují kontinuální spojení jednotlivých částí interpolovaného povrchu. Se spliny lze modifikovat část povrchu aniž bychom museli přepočítávat celý povrch (toto například neumožňují trendy). Pro interpolování linií se používá tzv. kubických splinů, pro interpolování povrchů se využívá jejich 2D analogie označované jako „thin plate splines“.

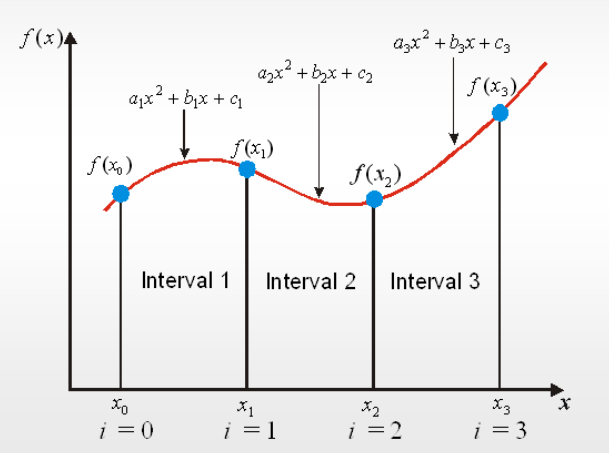
Obrázek 23: interpolace pomocí splinových funkcí

Kubické spliny používané ke shlazování čar dávají v případě interpolovaných povrchů značný počet chyb (výrazně malých či velkých hodnot), ať již v důsledku chyb měření či v důsledku komplexnosti interpolovaného povrchu. V tomto případě se na místo přesných splinů používá tzv. „thin plate splines“. Ty nahrazují části povrchů interpolované přesným splinem lokálně shlazenou průměrnou hodnotou. Povrch je interpolován tak, aby procházel co nejblíže měřeným bodům a také aby zachoval podmínku minimální křivosti. Spliny jsou tedy lokálním interpolátorem - používají v daném čase pouze několika málo bodů, na rozdíl od trendových funkcí a povrchů interpolovaných metodou vážené inverzní vzdálenosti spliny zachovávají řadu lokálních rysů interpolované proměnné. Spliny interpolované povrchy jsou často značně shlazené a jsou tedy vhodné pro interpolaci jevů, které se mění spojitě (např. tak vzduchu). Jistou nevýhodou splinových funkcí je, že produkují „falešná“ lokální minima a maxima.

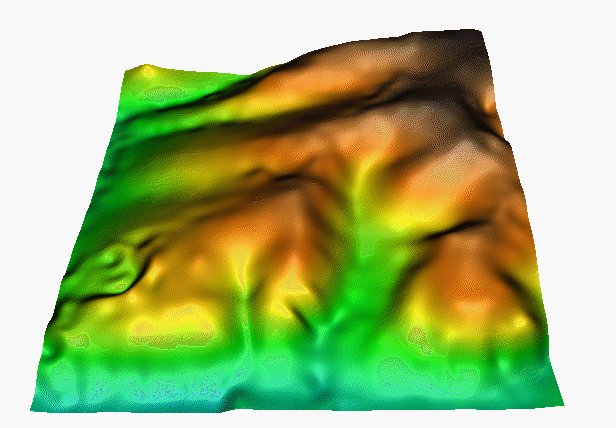
Obrázek 24: ukázka povrchu vytvořeného splinovými funkcemi (zdroj: http://fatra.cnr.ncsu.edu/~hmitaso/gmslab/)

Metody radiálních funkcí (RBF)

V prostředí ArcGIS jsou tyto metody interpolace označovány jako „radial basis functions“ (RBF). Jedná se o skupinu pěti exaktních interpolátorů označovaných: thin plate splines, spliny s tenzí, regularizované spliny, multikvadratické spliny, inverzní multikvadratické spliny. Tyto postupy k interpolaci využívají m.j. umělých neuronových sítí za podmínky mimimalizování křivosti povrchu (analogie „přetažení“ gumové membrány přes body v prostoru). Obrázek 25 ukazuje porovnání RBF metod s metodou inverzní vzdálenosti. Jak je z obrázku patrné, výsledkem interpolace metodou inverzní vzdálenosti nikdy nejsou body, které by byly větší než maximální hodnota v měřeném bodě resp. menší než minimální hodnota v měřeném bodě.

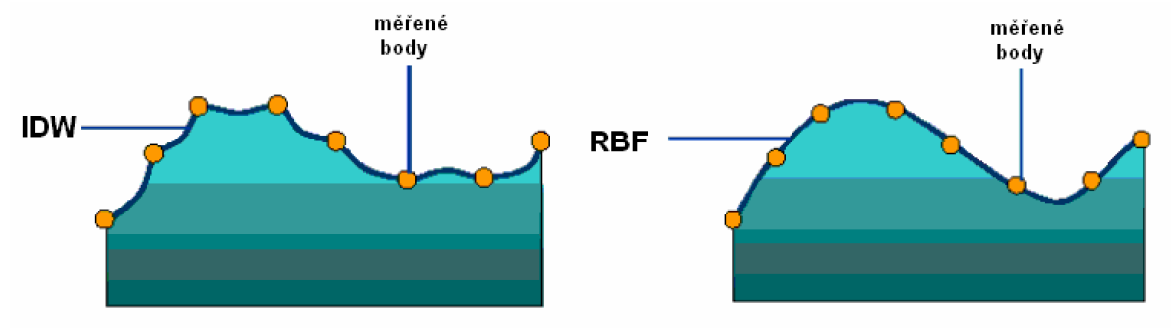
Obrázek 25: porovnání výsledků interpolace metodami splinových funkcí (RBF) a metodou inverzní vzdálenosti (zdroj: https://pro.arcgis.com/en/pro-app/help/analysis/geostatistical-analyst/how-radial-basis-functions-work.htm)

Parametry konkrétní interpolující funkce jsou optimalizovány výpočtem RMSPE. RBF jsou exaktní metodou a jsou vhodné pro hladké povrchy generované z velkého počtu bodů (např. modely terénu). Naopak se nehodí pro interpolaci jevů, které se v prostoru mění skokem (abrupt) a dále pro interpolaci jevů, u nichž existuje jistá míra nejistoty ohledně přesnosti měřených bodů.

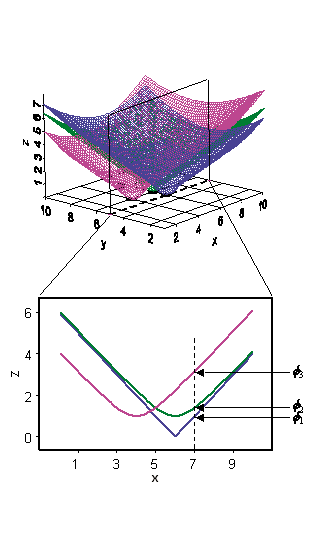
Obrázek 26: princip interpolace metodou multiquadric RBF (zdroj: https://pro.arcgis.com/en/pro-app/help/analysis/geostatistical-analyst/how-radial-basis-functions-work.htm)

RBF jsou funkce které se mění se vzdáleností od interpolovaného bodu. Jsou konstruovány pro každý měřený bod. Na obrázku 26 jsou vykresleny různou barvou tři RBF funkce pro tři body v prostoru. V tomto případě jsou RBF jednoduchou funkcí vzdálenosti od měřeného bodu a mají tvar obráceného kužele. Budeme uvažovat řez v rovině os \(X\) a \(Z\) pro bod \(y = 5\).

Předpokládejme, že budeme interpolovat bod o souřadnicích \(x = 7\) a \(y = 5\). Hodnotu každé RBF v predikovaném bodě můžeme odečíst z grafu jako \(\phi_1\), \(\phi_2\), \(\phi_3\). Prediktor má podobu váženého průměru, tedy:

\[w_1\phi_1+w_2\phi_2+w_3\phi_3+\dots\].

Doposud nebylo využito hodnot v měřených bodech. Proto váhy \(w_1\), \(w_2\), \(w_3\) jsou nalezeny na základě podmínky, že pokud je odhadován bod v bodě měření, je interpolován přesně. Tato podmínka umožňuje sestavit soustavu \(N\) rovnic o \(N\) neznámých, která má jednoznačné řešení. Všechny metody interpolace využívající RBF dávají velmi podobné výsledky. Metody mají možnost nastavit parametr, který ovlivňuje shlazení výsledného povrchu. U všech metod RBF platí, že čím větší hodnota vyhlazovacího parametru, tím více shlazený je povrch. Opačně je tomu pouze pro tzv. inverzní multiquadric RBF.

Nejčastěji využívanou je multikvadriková metoda (multiquadric RBF), která vychází z řešení následující rovnice:

\[B_{i}(x,y)=\sqrt{d_{i}(x,y)^{2}+R^{2}}\],

kde \(B_{i}(x,y)\) je radiální funkce vzdálenosti \(d_{i}(x,y)\), \(d_{i}(x,y)\) je relativní vzdálenost měřeného bodu v místě \(x_{i},y_{i}\) a \(R^{2}\) je vyhlazovací paramter.

Pro funkce \(B_{i}(x,y)\) jsou během výpočtu v každém interpolovaném bodě stanovovány váhy řešením soustavy lineárních rovnic.

Kriging

Je to lokální interpolátor, který optimalizuje výběr bodů okolí, ze kterých je odhadována nová hodnota. K této optimalizaci se provádí tzv. strukturní analýza založená na studiu tzv. semivariogramu a konstrukci teoretického modelu. Parametry tohoto modelu jsou použity ve vlastním krigování. Kriging je založen na odhadu závislosti průměrné změny v hodnotách studované veličiny a vzdálenosti měřených bodů. Strukturní analýze a metodě krigování je v této učebnici věnována zvláštní kapitola.

2.3 Interpolace ploch (area based)

Mnoho jevů se vztahuje k plošným jednotkám spíše než k bodům (hustota obyvatelstva států, kvalita pitné vody…). Metody řeší způsob, jakým lze odhadnout hodnoty jistého jevu na základě hodnot jiného jevu vázaných na plošné jednotky. Přitom mohou nastat dvě situace:

1. plošné jednotky se shodují,
2. zdrojové jednotky jsou podmnožinou (nested) jednotek výstupních.

Metody lze dělit do dvou skupin:

1. metody zachovávající objem studovaného jevu (volume preserving),
2. metody nezachovávající objem studovaného jevu (non-volume preserving).

Metody nezachovávající objem studovaného jevu (non-volume preserving) Příklad – mapa A vyjadřuje celkový počet obyvatel ve čtyřech administrativních jednotkách určitého území. Mapa B potom záplavovou oblast kolem vodního toku. Cílem je zjistit, jaká je hustota obyvatelstva uvnitř záplavové zóny. Mapa C zobrazuje hustotu obyvatel v administrativních jednotkách, mapa D - interpolovaný grid hustoty obyvatel, mapa E - odhad celkového počtu obyvatel v gridu a mapa F počet obyvatel v záplavové zóně.

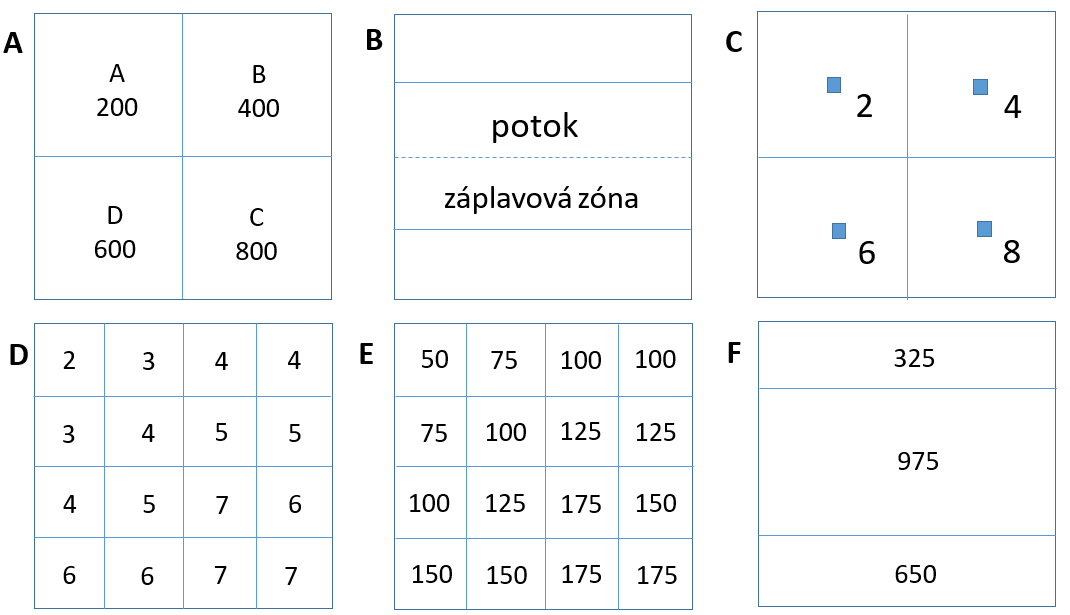
Obrázek 27: princip prostorové interpolace nezachovávající objem studovaného jevu (zdroj: upraveno podle Dobrovolného, 2010)

Postup:

1. výpočet hustoty obyvatelstva pro každou plochu,
2. určení centroidu každé plochy,
3. interpolace hustoty obyvatelstva výše popsanými metodami.

Metody zachovávající objem studovaného jevu (volume preserving)

Provede se překrytí cílových zón (oblastí) přes oblasti zdrojové a určí se poměrná část cílové zóny, která spadá do zóny zdrojové. Celková hodnota atributu v cílové zóně je určena v závislosti na plošném zastoupení zón zdrojových.

Pycnophylatic method

Jeden z hlavních problémů metody thiessenových polygonů je, že měřený prvek se považuje za homogenní v rámci jedné třídy, veškeré prostorové změny jsou vázány na hranice. V případě spojitých či relativně spojitých prvků jde o naprosto nevhodný způsob interpolace.

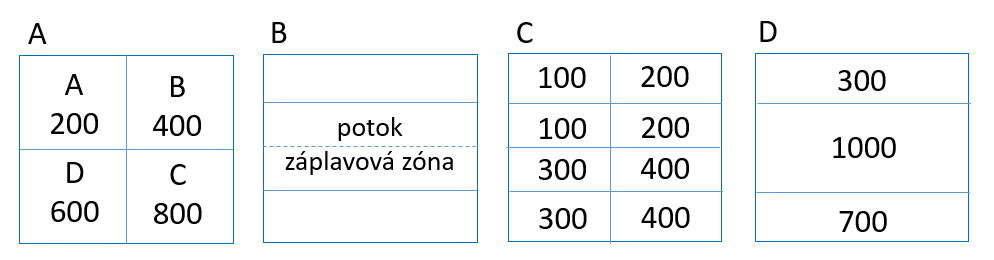
Obrázek 28: princip prostorové interpolace zachovávající objem studovaného jevu (zdroj: upraveno podle Dobrovolného, 2010)

Modifikací je metoda, která v rámci každé třídy zachovává sumu studovaného prvku, avšak dovoluje kontinuální změnu směrem k hranicím každé třídy. Metoda bere v úvahu hodnotu atributu sousedních tříd. Nepředpokládá se existence bariér a hodnoty sousedních tříd jsou shlazeny bez skokových změn v hodnotách daného atributu pomocí pravděpodobnostní funkce (density function). Metoda byla použita na demografická data. Jde o neexaktní interpolátor. Minimální i maximální hodnoty vypočtené touto metodou jsou výrazně menší resp. větší než skutečně naměřené hodnoty.